Целью работы: Какие неравносторонние четырехугольники разделить на три равносторонние треугольника. Эти действия равны к открытиям, так как до сегодняшнего дна такие задачи не решались.
Для достижения этой цели, необходимо учитывать следующее:
1. Среди различных четырехугольников для нашего доклада были выбраны те четырехугольники которых можно разделить.
2. Каждый прямоугольник из доклада выявили ряд удовлетворяющих четырехугольников
Первоначальная гипотеза: Несмотря на неисследванность этой темы, мы считаем, предоставить необходимые цифры.
Практическая значимость:
Данное исследование является предметом внутренних законов математики, потому что в области математики и математики, используемых другими разделами практики.
Научная значимость проекта, поскольку она обеспечивает качества неизвестные до сих пор. Применяют как это означает, что проект может быть использовать для создания различного рода мозайк, паркетов, и в сфере шитья корпеше лоскутной мозайкойк. С другой стороны, если мы рассмотрим результаты проекта могут использовать дополнительные классы. Четырехугольники из областей, где практика в момент выделения 3-х равнобедренных треугольников требование.
Методы исследования: анализ, синтез, индукция, дедукция.
Актуальность темы
Есть два эффективных способов выучить математику. Первый: Подход к различным проблемам. Второй: Подход увеличивает возможность использования путем углубления развития теории математики. Второй подход заключается в общий подход, а не первым, это может привести к целому ряду докладов, чтобы доказать теории. Наш вариант – второй подход.
Целью объекта исследования проекта в преамбуле, новизна и практическое значение начальной гипотезы и методы исследования.
Основной раздел целей, сделанных.
И, наконец, до завершения работы, выполненной и кратко, как это может продолжаться.
Проект оборудован списком ссылок.
Параллелограмм
1. ABCD параллелограмм три треугольника tenbuyirli: в AVD, кровать, EDC.
Параллелограмм равно противоположных углах a + β + γ = β + γ + 180-2anemese 3α = 180 (1) уравнения. За счет применения этого правила в краях А и С α = 180-2γ (2) знаю, что. Две параллельные линии появились убиты usinsimen равно внутренних углах поперечного р = а (3). Кроме того, мы имеем следующие уравнения:
γ + 3α = 180
α = 180-2γ
β = α
Второе значение выражается уравнением клиновидного первого уравнения, и следующее уравнение: γ + 540-6γ = 180. В результате, γ = 720. бета = 360, α = 360.
Блоки, предусмотренные проектом в целом, я изучал только 1 квадрат, потому как время для решения задачи ограничено.
Трапеция
Трапецию ABCD разделим на равносторонние треугольники: ABD, BED, BCE.
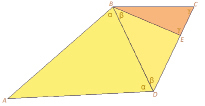
Рис. 1
В одной стороне трапеции сумма углов 180° по этой причине α + β + γ = α-β + 2γ или γ = 2β (1) . Так как угол BDC равносторонний выходит равенство 2γ + β или β = 3 γ – 180(2) .
Если при пересечение двух прямых третьей внутренние односторонние углы равны, то берем равенство α = β + 180-2γ (3) Итого получаем такого вида систему линейного уравнения:
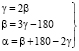
С третьего уравнения вместо β подставляем значения с уравнения два, и получаем α = 180-2γ + 3γ-180 или α = γ. В первом уравнении γ- выражаем через β и все подставляем во второе уравнение, и того: β = 6β-180. И так, β = 36º, α = 72º и γ = 72º.
Ромб
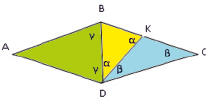
Рис. 2
1. Ромб ABCD разделим на равносторонние треугольники:
ΔADB, ΔBKD, ΔKDC.
Так как противолежащие углы равны γ + 180º-2α = γ + α + β или β = 180º-3α получим (1) уравнение.
Помимо этойго правилы используем, что можно использовать два угла = 180º-2γ и получаем (2) уравнение, угол ‹F плоский угол, т.е.1800, и того α + 180º-2β = 1800 или α = 2β получаем (3) уравнение. Получаем следующую систему уравнении:
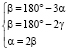
В третьем уравнении вместо значении α подставляем в первое уравнение, β = 180º – 6β. Итого 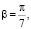
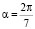 и
и 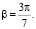
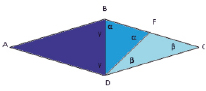
Рис. 3
Библиографическая ссылка
Есилжан Ж. ДЕЛЕНИЕ НЕКОТОРЫХ ЧЕТЫРЕХУГОЛЬНИКОВ НА РАВНОСТОРОННИЕ ТРЕХУГОЛЬНИКИ // Старт в науке. 2017. № 4-1. ;URL: https://science-start.ru/ru/article/view?id=675 (дата обращения: 08.12.2025).
