• Авторы
• Файлы

Акамсина Т.В. 1

---

1 МОУ СОШ № 14, г. Комсомольск-на-Амуре

Статья в формате PDF

0 KB

Цели урока:

Образовательная: добиться усвоения теоремы Пифагора, научить вычислять неизвестную сторону прямоугольного треугольника по двум известным, научить применять теорему Пифагора к решению простейших задач

Развивающая: способствовать развитию способности к сопоставлению, наблюдательности, внимания, развитие способности к аналитико-синтетическому мышлению, расширение кругозора

Воспитательная: формирование потребности в знаниях, интереса к математике, воспитание чувства взаимопомощи, коллективизма

Тип урока: урок изложения нового материала

Оборудование: компьютер, мультимедийный проектор, презентация к уроку

План урока:

1. Организационный момент
2. Устные упражнения. Актуализация знаний
3. Исследовательская работа, поиск неизвестной стороны прямоугольного треугольника. Формулировка и доказательство теоремы
4. Историческая справка
5. Закрепление изложенного материала через решение задач. Исторические задачи
6. Задание на дом, подведение итогов урока.
7. Рефлексия

Ход урока:

Организационный момент

Здравствуйте, ребята! Садитесь! Работать на уроке не ленитесь! Тетради и ручки в миг взяли, число на полях записали!

И чтобы нам с вами определиться, чему на уроке должны научиться, внимательно ты на экран посмотри, площадь фигуры каждой найди!

Устные упражнения

Предлагаю вам решить несколько устных задач

Слайд 1

1. Найдите площадь квадрата со стороной 3 см; 1,2 мм; 5\7 м; а см

2. Чему равна площадь домика? Sтр = 5 см2; Sпр =20 см2

3. Раскройте скобки: (а+в)2; (3+х)2

Слайд 2

4. Найдите площадь прямоугольного

треугольника с катетами 9 см и 6 см;

2,2 м и 5 см; а см и в см.

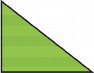
Слайд 3

Найдите площадь прямоугольного треугольника с гипотенузой 5 и катетом 3.

- Сможем ли мы найти площадь? Что нам для этого нужно? (Второй катет)

- на сегодняшний день мы знаем как найти третью сторону прямоугольного треугольника? (нет). Какова тогда будет цель нашего урока?

Слайд 4

Записали в тетрадь цель: научиться находить неизвестную сторону прямоугольного треугольника

Исследовательская работа, поиск неизвестной стороны прямоугольного треугольника. Формулировка и доказательство теоремы.Итак, ребята, поиск ответа на наш вопрос мы начнем со следующей работы.

Всем треугольники равные прямоугольные раздам,

Себе и вам вопрос задам:

Возможно ли их так расположить,

Чтобы квадрат в итоге получить?

Достаем из конвертов белый листочек и 4 треугольника, на нем пробуем сложить из них квадрат. Кто первый догадается, получит пятерку!

Слайд 5

Всё! Получился у ….. квадрат! Чему я несказанно рад!

Внимательно на доску посмотрите, площадь квадрата такого найдите!

Ребята, все сложите таким образом квадрат и приклейте на белый листок. Подпишите катеты и гипотенузу.

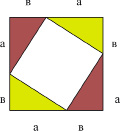
Найдем площадь этого квадрата.

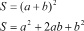
1. Площадь квадрата равна

- Каким образом ещё можно найти площадь исходного квадрата?

- Почему равны получившийся четырехугольник - квадрат?

2. С другой стороны,

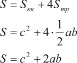
3. Приравняем получившиеся равенства:

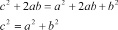
Как сформулировать полученное равенство?

Слайд 6

Теорема: Квадрат гипотенузы равен сумме квадратов катетов!

Слайд 7

Данная теорема получила название теоремы Пифагора! Итак, запишем тему урока в тетрадь.

Историческая справка

Слайд 8

Геометрия обладает двумя великими сокровищами.

Первое – это теорема Пифагора…» Иоганн Кеплер

О Пифагоре сохранились десятки легенд и мифов, с его именем связано многое в математике, и в первую очередь, конечно, теорема носящая его имя, которая занимает важнейшее место в школьном курсе геометрии.

Слайд 9

Знаменитый древнегреческий философ и математик Пифагор Самосский родился на острове Самос, недалеко от Греции в 580 году до н. э. По античным свидетельствам он был красив и обладал незаурядными способностями. Совсем юношей он покинул родину, прошел по дорогам Египта и 12 лет жил в Вавилоне. После возвращения домой Пифагор переселился в Италию, затем в Сицилию.

Слайд 10

Здесь в Кретоне, рождается школа Пифагора. В пифагорейской школе занимались изучением чисел и их свойств, много внимания уделяли музыке, живописи, физическому развитию, здоровью. Пифагор и его ученики были трудолюбивы и аскетичны.

Слайд 11

Шутливая формулировка Теоремы ПИФАГОРА:

Если дан нам треугольник

И притом с прямым углом

То квадрат гипотенузы

Мы всегда легко найдём:

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путём

К результату мы придём.

Видео

Почему же появилась необходимость находить неизвестную сторону прямоугольного треугольника? Посмотрим видео.

Закрепление изложенного материала через решение задач. Исторические задачи

Слайд 12

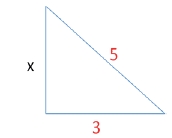
Найдите гипотенузу: (Учитель у доски объясняет применение теоремы пифагора)

х²= 4²+3²=16+9=25, х=5

Слайд 13

Вернёмся к задаче, которую мы не смогли решить в начале урока: Найдите площадь прямоугольного треугольника с гипотенузой 5 и катетом 3.

По задаче 1 имеем, что х=4. Отсюда S=0.5*4*3=6

Слайд 14

Египетский треугольник

Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5. Особенностью такого треугольника, известной ещё со времён античности, является то, что при таком отношении сторон теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть 9:16:25. Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.

Решение исторических задач

Слайд 15

1.Задача индийского математика XII века Бхаскары (устно)

«На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.Бедный тополь упал. И угол прямойС теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи:У тополя как велика высота?»

АВ=5 футов, СД=5+3=8 футов

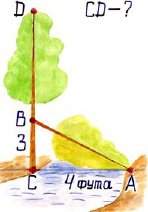
Ответ: 8 футов

Слайд 16

2. Задача из учебника «Арифметика» Леонтия Магницкого

«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».

Как понять условие и вопрос задачи? Что является гипотенузой и катетами? Какой элемент нужно найти? (решает ученик у доски)

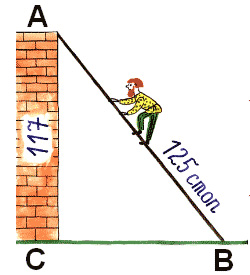
ВС2=1252-1172=15625-13689=1936, ВС=44 стоп

Слайд 17

3.Задача из китайской «Математики в девяти книгах» (дополнительно)

«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?».

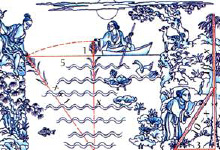
(х+1)²=х²+5², х²+2х+1-х²=25, 2х=24, х=12.

Ответ: глубина воды 12 чи, длина камыша 13 чи.

6. Задание на дом, подведение итогов урока.

Подведение итогов урока:

- Какую цель мы ставили в начале урока?

- Научились ли вы находить неизвестные стороны прямоугольного треугольника?

- Какое открытие нам в этом помогло?

- Давайте еще раз сформулируем теорему Пифагора

Слайд 18

Домашнее задание:

- Выучить теорему Пифагора с доказательством

- Задачи из учебника № 483 в, г; № 484 в, г.

- Для более подготовленных учащихся: найти другие доказательства теоремы Пифагора, выучить одно из них.

Слайд 19

Рефлексия

Дерево успеха. Каждый листочек имеет свой определенный цвет: зеленый — все сделал правильно, желтый — встретились трудности, красный — много ошибок. Каждый ученик наряжает свое дерево соответствующими листочками.

Библиографическая ссылка