Мы вращаем кубик, а кубик скручивает нас.
Эрнё Рубик
Кубик Рубика – это классика среди пространственных головоломок, которую 1974 году преподаватель архитектуры из Венгрии Эрнё Рубик изобрел. Вот уже несколько десятков лет кубик с разноцветными гранями занимает умы детей и взрослых по всему миру! Интерес к этой головоломке подогревается и постоянным усовершенствованием механизма, а также появлением все новых и новых разновидностей традиционного кубика Рубика.
Цель исследования: Выяснить уникальную механическую систему кубика Рубика 3×3×3, предложенную Э.Рубиком.
Выяснить уникальные механические системы кубиков Рубика 2×2×2, 4×4×4, 5×5×5, 6×6×6, 7×7×7, 11×11×11 и 17×17×17 сравнить с внутренним механизмом классического кубика Рубика 3×3×3.
Задачи:
1. Изучить уникальный внутренний механизм кубика Рубика 3×3×3.
2. Изучить уникальные механические системы кубиков Рубика 2×2×2, 4×4×4, 5×5×5, 6×6×6, 7×7×7, 11×11×11 и 17×17×17 сравнить с внутренним механизмом классического кубика Рубика 3×3×3.
3. Сделать выводы.
Материалы и Методы. Методы: Изучение литературы и Интернет-ресурсов; Экспериментальный метод; Анализирующая деятельность.
Материалы: кубики Рубика 3×3×3; 2×2×2; 4×4×4; 5×5×5 и 6×6×6.
Этот вопрос меня заинтересовал, в связи с тем, что я увлечен сборкой кубика Рубика (научился собирать 2×2×2; 3x3x3;4x4x4;5x5x5 и 6×6×6 и не буду останавливаться на этом) а вот с механическими системами незнаком.
Классический кубик Рубик 3×3×3
Кубик Рубика – это объёмная головоломка, представляющая собой стереотипный механизм в виде пластмассового куба, размером 3 на 3 квадрата. Каждая из 6 граней, состоит из девяти квадратов (всего в головоломке 54 квадрата) и имеет свой отдельный цвет. Классические цвета кубика Рубика: синий, белый, красный, зеленый, желтый, оранжевый.
Расположены грани всегда следующим образом:
• белый напротив жёлтого,
• красный напротив оранжевого,
• синий напротив зелёного.

Для изучения внутреннего механизма кубика Рубика 3×3×3 классического и усовершенствованного – я их разобрал на части, а затем сложил обратно [9].
При этом выяснил следующее.
Классический кубик Рубика 3×3×3.
Внешне он представляет из себя куб, как бы разрезанный на 27 маленьких кубиков, но в действительности их 26. Но эти 26 кубиков назвать кубиками можно лишь условно, все они имеют разные выпуклости, выемки и шипы, благодаря которым они держаться друг за друга и перемещаются. И еще их все можно разделить на три группы, в зависимости от того где они располагаются на гранях большого куба:
Шесть маленьких кубиков (Центральные кубики) -расположены они в центре каждой грани большого куба. Основа куба – крест, к тонким осям которого прикреплены на винтах 6 центральных кубиков. Окрашены они только с одной стороны, с которой и видны.
Все центральные кубики связаны между собой тремя осями. Каждая пара противоположно расположенных центральных кубиков вращается только вокруг одной своей оси. Центра-это единственная составляющая, которая не может перемещаться, т.е. центральные кубики нельзя сдвинуть с места. Центральные сегменты определяют исходный цвет соответствующей грани. Если на данной стороне центральный кубик белый, значит. Это будущая белая грань. Именно этот факт и необходимо учитывать при сборке граней.
а б

Рис. 1. а – центральные кубики; б – крест и на нем крепятся центральные кубики
Центральные части или просто центры – части с одним цветом. Всего у кубика 6 центральных частей, расположенных в центре каждой грани. Центральные части не двигаются и представляют цвета их граней.
Восемь маленьких кубиков (Угловые кубики), находящихся на углах большого куба, окрашены одновременно тремя разными цветами с трех видимых сторон. Все 8 угловых кубика могут перемещаться.




Рис. 2. Угловые кубики
Двенадцать маленьких кубиков (Средние, Бортовые кубики), расположены на середине ребер большого куба, покрашенные только с двух видимых сторон. Именно они соединяют центра. Все 12 бортовых кубика также могут перемещаться. Т.О. Сколько ни верти ряды кубиков относительно друг друга, угловые кубики всегда останутся угловыми, бортовые – бортовыми, ацентральные – центральными. Эту очевидную истину иногда в шуткуназывают основной теоремой «кубологии».




Рис. 3. Бортовые кубики
Таким образом, основа куба – жесткий каркас: трехмерная крестовина, которая находиться в центре конструкции и на ней вращаются 6 центральных кубиков, прикрепленные к тонким осям креста на винтах. Они могут вращаться вместе с гранью, которая перемещается заодно с центральным кубиком данном грани. В некоторых моделях, есть пружинка, одетая на тонкий конец креста, позволяющая оттягивать при повороте поворачиваемый слой кубиков.
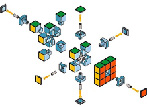
Рис. 4. Схема механизма классического кубика Рубика 3×3×3
Рис. 5. Пружинка
В центральных и бортовых кубиках с внутренней стороны сделаны вырезки таким образом, что получается полость в виде объединения трёх цилиндров. Кроме этого, на бортовых и угловых кубиках имеются выпуклости разной формы. Они образуют фрагмент цилиндра, который плотно входит в упомянутую выше полость. С помощью такой конструкции грани кубика свободно вращаются с внутренних сторон центральные, бортовые и угловые кубики имеют различные вырезы.
Механическая система кубика Рубика уникальна по своей простоте и изяществу.



Рис. 6. Внутреннее соединение кубиков
Карманный кубик Рубик 2×2×2
Данная головоломка – это упрощённая версия обычного классического кубика Рубика. Называется она по-разному, например, карманный кубик или мини кубик, детский. Карманный кубик был запатентован Эрне Рубиком 29 марта 1983 года (Патент US 4,378,117). Головоломка состоит из 8 более мелких кубиков, собранных в один большой 2×2×2 куб. Мини кубик – это такой же кубик Рубика, у которого отсутствуют центры и ребра, т.е. можно считать, что они всегда собраны.

Рис. 7. Карманный кубик
Каждую грань можно вращать, меняя тем самым положение 4 маленьких кубиков на грани. Каждая из 6 граней головоломки имеет свой цвет и которые располагаются также как и у классического кубика Рубика 3×3×3. Данный куб собирается очень легко, так как имеет всего две формулы сборки. Следовательно, внутреннее устройство у него проще чем у других кубиков.
В основе куба лежит шарик из шести круглых элементов с пазами. Внутри шарика находится стандартная крестовина, такая же, как и в традиционном кубике Рубика 3×3. По сути, этот шарик обладает точно такой же конструкцией, как и кубик Рубика 3×3, только его центральные элементы гораздо крупнее, реберные наоборот меньше, а угловые выполнены в виде зацепов для элементов куба 2×2. Элементы самого кубика 2×2 соединяются как раз с этими зацепами. Так что помните, что собирая кубик 2×2, вы невольно собираете еще и кубик 3×3 внутри него!



Рис. 8. Внутреннее устройство карманного кубика
Реванш кубик Рубика 4×4×4
Рассмотрим кубик Рубика 4×4×4. Называется он Реванш Рубик, можно встретить название “Месть Рубика”. Механизм кубика 4×4 был запатентован Петером Себестени (Peter Sebesteny) 20 декабря 1983 года, (Патент US 4,421,311). Это усложненная разновидность классической головоломки. Каждая грань кубика состоит не из 3, а из 4 элементов, что полностью меняет алгоритмы сборки, так с этим кубиком придется повозиться! К изобретению этого и последующих кубиков Э.Рубик к никакого отношения не имеет, но их по привычке называют кубиками Рубика. Каждая из 6 граней головоломки имеет свой цвет и которые располагаются также как и у классического кубика Рубика 3×3×3. Прежде, чем собирать кубик Рубика 4×4, научитесь собирать классический кубик 3×3, т.к. сборка кубика 4×4 состоит из тех же алгоритмов, что и 3×3, но дополнена несколькими новыми формулами. В основе внутреннего механизма этого кубика находиться также крестовина:


Рис. 9. Внутренне устройство Реванш кубика

Вместо одного центрального кубика (в отличии от кубика Рубика 3×3×3). На каждой грани их стало 4. Таким образом у кубика Рубика 4×4 – 24 центральных кубика. Но у головоломки 4×4, центральные кубики всех сторон подвижны (и это свойство всех четных кубов: 4×4, 6×6, 8х8 и т.д. В отличие от Рубика 3×3и других нечетных кубов: 5×5, 7×7 и т.д., в которых цвет центральной части зафиксирован. Поэтому в четных кубиках центры не могут быть сразу использованы, в качестве опорных точек и именно это свойство и делает сборку четных кубов более сложной, в отличии от сборки нечетных кубов (где центры нужно использовать для определения цветов граней).
а б
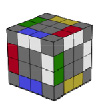
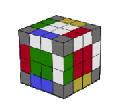
Рис. 10. Виды кубиков: а – Реберных кубиков 24 штук, каждая рёберная часть окрашена в 2 цвета; б – угловых кубиков – 8 штук и угловая часть окрашена в 3 цвета
Профессорский кубик Рубика 5×5×5
Рассмотрим кубик Рубика 5×5×5. Механизм кубика 5×5 был запатентован Удо Крелл (Udo Krell) 15 июля 1986, (Патент US 4,600,199). Это усложненная разновидность классической головоломки. Каждая грань кубика состоит не из 3, а из 5 элементов, и относиться к нечетным кубам. Цвета граней располагаются аналогично классическому кубику Рубика 3×3×3. Для того чтобы легко научиться собирать кубик Рубика 5×5, нужно уметь собирать классический кубик 3×3. Внутренний механизм состоит из крестовины (как и у классического кубика Рубика).
а б в

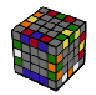

Рис. 11. Виды кубиков: а – 6 центров кубика на каждой грани, всего центральных кубиков – 36 штук; б – реберных кубиков – 24 шт, каждая рёберная часть окрашена в 2 цвета; в – угловых кубиков – 8 штук и угловая часть окрашена в 3 цвета


Рис. 12. Механизм классического профессорского кубика
Кубики Рубик 6×6×6
Следующими идет четный куб 6×6×6. Куб 6×6 относится к классу профессиональных – его (и остальные кубики) обычно приобретают спидкуберы, уже освоившие скоростную сборку 3, 4 и 5-слоевых головоломок. Основа внутреннего механизма куба является также крест. Цвета граней располагаются аналогично классическому кубику Рубика 3×3×3. Прежде, чем собирать кубик Рубика 6x6, научитесь собирать классический кубик 3×3.


Рис. 13. Механизм кубика 6×6×6
Остальные кубики Рубики
Кубики 7×7×7 и 11×11×11 относиться к нечетным кубам, в основе внутреннего устройства лежит вновь крестовина и его сборка также основана на умении собирать классический кубик Рубика 3×3. Цвета граней располагаются аналогично классическому кубику Рубика 3×3×3.

Рис. 14. Механизм кубика 11×11×11
Многим весьма непросто решить классическую 3×3×3 головоломку Кубик Рубика, но есть люди, которым даже версии 5×5×5, 6×6×6 …11×11×11 кажутся слишком простыми. По всей видимости, это и привело к появлению невероятной версии 17×17×17. В 2011 году дизайнер головоломок Оскар Ван Девентер создал самый большой кубик Рубика в мире – 17×17×17. Куб состоит из 1734 цветных клеток и имеет сложнейший механизм! Каждая из 6 граней этой головоломки имеет свой цвет и которые располагаются также как и у классического кубика Рубика 3×3×3. Чтобы собрать такой куб используют «метод сокращения». Он заключается в том, чтобы разложить площадь кубика на квадраты 3×3 и решать их один за другим. Получатся прежде, чем собирать кубик Рубика 17x17, нужно вновь научиться собирать классический кубик 3×3×3.
Результаты:
1. Выяснил уникальную механическую систему классического кубика Рубика 3×3×3 и сравнил ее с механической системой усовершенствованного и скоростного кубика Рубика 3×3×3. Это знание внутреннего устройства кубика Рубика позволяет мне еще быстрее его собирать.
2. Понял, что для сборки кубиков Рубика, с любым количеством ячеек, главное нужно идеально научиться собирать классический куб 3×3×3.
3. У всех рассмотренных кубиков Рубика классический внутренний механизм это крест – основа куба.
4. Выяснил, чем отличаются кубики с четным количеством (4×4, 6×6, 8х8 и т.д) ячеек от кубиков с нечетным количеством: у четных кубиков-центра подвижные, у нечетных кубиков (3×3, 5×5, 7×7 и т.д) –неподвижны, т.е. по центральному кубику легко ориентироваться какого цвета должна получиться собираемая грань. А вот у четных кубиков, к сожалению, из-за подвижных цетров –ориентироваться нельзя. Именно поэтому четные кубики в сборке сложнее, чем нечетные кубики.
5. У всех кубиков, с любым количеством ячеек есть центральные кубики (окрашенные только с одной стороны), есть угловые (окрашенные с трех сторон) и реберные кубики(окрашенные с двух сторон). Количество угловых кубиков у всех одинаковое – 8 штук, а вот количество центральных и реберных различное.
6. У всех головоломок цвет граней и их расположение полностью совпадает с классическим кубиком Рубика 3×3×3.
7. Благодаря кубику Рубика развивается: моторика рук, логика, память, дикция, усидчивость, быстрое мышление.
Я нашел решение своим вопросам и советую каждому не останавливаться перед трудностями, а искать решение!
Библиографическая ссылка
Зайцев А.А. МЕХАНИЧЕСКИЕ СИСТЕМЫ КУБИКОВ РУБИКА // Старт в науке. 2019. № 4-4. ;URL: https://science-start.ru/ru/article/view?id=1772 (дата обращения: 13.03.2026).
