Основная проблема исследования. Биология с разных сторон изучает законы функционирования живых объектов, самым сложным из которых можно считать человека. В современной медицине широко используются различные программы и имитационные модели, которые позволяют оценивать работу органов и систем организма человека. При этом особое внимание уделяется сердцу. В большинстве случаев, диагностика жизнедеятельности сердца выполняется по результатам регистрации на стандартных отведениях электрических потенциалов, образующихся при работе сердца – ЭКГ (рис. 1).
Как видно из рис. 1, о большинстве заболеваний сердца может сообщить Т зубец. Однако механизм его возникновения в настоящее время до конца не изучен. Согласно устоявшихся представлений [1, 2], электрофизическая модель сердца описывает возникновение только R зубца (рис. 2)
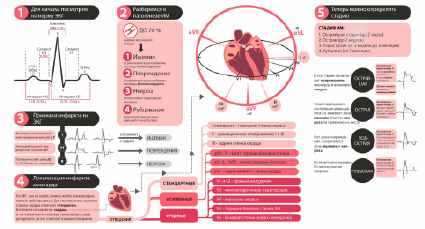
Рис. 1. Находим инфаркт Миокарда на ЭКГ [1]
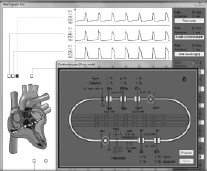
Рис. 2. Фрагмент работы электрофизиологической модели сердца [2]
При этом механизм формирования Т зубца, отражающего состояние сердца остается неизученным. Изучение механизма формирования Т зубца в сигнале ЭКГ составляет основную проблему исследования в статье.
Актуальность исследования. В настоящее время существует много моделей описывающих электрическую активность сердца [3, 4]. Например, в резистивной модели сердечнососудистой системы, за аналог сердца принимался источник несинусоидального переменного электрического напряжения связанный с выпрямителем тока, представляющим из себя сердечный клапан. В модели электрической активности сердца для моделирования электрической активности возбудимых волокон сердца использовано приближение в виде генератора переменного электрического поля. Однако все эти модели основаны на представлении о том, что меридиан сердца представляет из себя кольцо (см. рис.1). В то же время, результаты современных исследований [5, 6] показали, что миокард сердца имеет топологию Мебиуса (рис. 3).

Рис. 3. Меридиан Сердца [6]
Это делает актуальным оценку влияния неориентированной поверхности (см. рис. 3) на распространение электрического потенциала, регистрируемого в стандартных отведениях при снятии ЭКГ.
Цель исследования. Определить, влияет ли топология миокарда сердца на формирование Т зубца в ЭКГ.
Гипотеза. Принимаем, что в синусовом узле сердца периодически вырабатывается электрический R-импульс (см. рис. 1). В этом приближении, в качестве гипотезы полагаем, что электрический импульс по мере своего движения по замкнутому меридиану сердца ослабевает из электрического сопротивления тканей миокарда и «набегает» на периодический сигнал (R зубец), накладываясь и вызывая появление в сигнале ЭКГ Т зубца.
Задачи работы:
а – определить, за какое время электрический ток пройдет по кольцевому контуру;
б – оценить влияния неориентированной поверхности на время обхода контура.
Предмет исследования. Известно, что меридиан сердца [6] представляет собой фигуру (см. рис. 3) с поверхностью Мебиуса. Результаты 3D сканирования миокарда показали, что он имеет переменные размеры: длина 60 см, ширина 8–10 см, толщина 0,5–2 см [7]. На основании полученных данных в работе принимаем, что морфологически-подобная модель миокарда c масштабируемыми электрофизическими характеристиками, может быть выполнена из разделенного между собой слоем диэлектрика проводящего гибкого материала толщиной 0,1 мм (рис. 4) длиной 60 см и шириной 8 см.
а б


Рис. 4. Образец имитатор: а – в форме кольца; б – в форме неориентированной поверхности
Основная часть
В соответствии с выдвинутой гипотезой, определим, за какое время импульс электрического тока пройдет по окружности экспериментальных образцов. Известно, что электрическое поле это одна из составляющих частей электромагнитного поля [8] и, следовательно при приложении разности потенциалов к изолированным обкладкам кольца, электрический импульс будет распространяется со скоростью света с=300 000 км/с. Таким образом, импульс электрического сигнала пройдет по окружности образца за время:
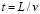 , (1)
, (1)
где L – длина окружности; v – скорость распространения электромагнитной волны.
Рассмотрим случай кольца (см. рис. 4,а). Длина окружности, т.е. длина проводящего слоя составляет 60 см. Проводники между собой не замкнуты, т.е. расстояние L которое будет преодолеваться будет равно длине окружности и составит 60 см. При этом, при приложении разности потенциалов источник электрического сигнала будет работать в режиме холостого хода. Расчет по формуле (1) показывает, что время t1, за которое электрический ток пройдет по кольцевому контуру составит:
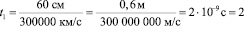 .
.
Если в качестве образца использовать кольцо с топологией Мебиуса (см. рис. 4,б), тогда следует учитывать особенные свойства, присущие ленте Мебиуса свернутой в кольцо. В частности А. Мебиус в своем труде «Об объеме многогранников» описал геометрическую поверхность, названную затем в его честь, обладающую всего одной стороной. Т.е. если взять ленту и закрасить одну сторону одним цветом, а другую – другим, тогда не важно, в каком месте и направлении было начато окрашивание, вся фигура будет закрашена одним цветом. Таким образом, при приложении разности потенциалов к разделенным слоем диэлектрика полосам (см. рис. 4,б) источник электрического сигнала будет работать в режиме короткого замыкания, а длина проходимого электрическим током контура будет удваиваться. Выполним по формуле (1) расчет времени t2, за которое электрический ток пройдет по контуру в форме неориентированной поверхности с учетом того, что для рассматриваемого случая L=120 см:
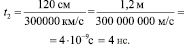
Результаты расчета позволяют оценить влияние неориентированной поверхности на время обхода контура. Видно, что время t2 в два раза больше по сравнению с t1. Из результатов расчета времени t1, t2 так же видно, что электрический импульс действительно может «набегать» на периодический сигнал (R зубец) (см. рис. 1). Однако вызывать появление в сигнале ЭКГ Т зубца он не может, т.к. время, через которое появляется Т зубец составляет 0,35–0,44 с, а даже в приближении топологии Мебиуса время t2 в 108 раз длиннее.
В то же время известно, что отношение скорости электромагнитной воны волны в вакууме c к скорости ее распространения в системе v: n=c/v – называется коэффициентом замедления. Эта характеристика имеет тот же физический смысл, что и показатель преломления прозрачной среды для света [9]. И если предположить, что реальные ткани миокарда сердца по своим токопроводящим свойствам отличаются от использованных проводников (см. рис. 4), и в сердце на пути электрического тока имеется замедляющая система (линию задержки), то тогда становится возможным существенно понизить скорость распространения электрического поля, а значит, и тока. Поэтому ЭКГ в соответствующем отведении покажет появление Т зубца не сразу после появления R зубца цепи. И двухкратное увеличение времени t2 по сравнению с t1 как раз и показывает на повреждение миокарда, когда T зубец сливается с R зубцом (см. рис. 1)
Рассмотрим еще один механизм, который может вызывать появление импульсов в сигнале ЭКГ. Известно, что изменение электрического поля распространяется по проводнику со скоростью электромагнитной волны, активируя электроны в цепи. Но сами электроны движутся гораздо медленнее. Скорость упорядоченного движения электронов (или в случае сердца каких либо других носителей заряда) принято называть дрейфовой скоростью:
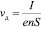 , (2)
, (2)
где I – сила тока; е – заряд электрона е=1,6?10–19 Кл; n – концентрация атомов, в металлах n = 1028–1029 м–3; S – поперечное сечение проводника.
Оценим дрейфовую скорость. Известно, что сила тока в 100 мА считается смертельно опасной и вызывает остановку сердца [10]. На основании этого принимаем, что в здоровом сердце протекает ток 10 мА. Для использованных образцов (см. рис. 4) поперечное сечение S составляет 8 мм2. Результаты расчета дрейфовой скорости по формуле (2):
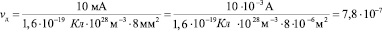 м/c.
м/c.
Расчет по формуле (1) показывает, что время t1д, за которое электроны пройдут по кольцевому контуру составит:
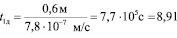 сут.
сут.
А для неориентированного контура время t2д составит:
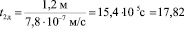 сут.
сут.
Видно, что дрейфовая скорость вызывать появление в сигнале ЭКГ Т зубца он не может, т.к. время, через которое появляется «набегание» сигнала составляет несколько недель.
Заключение
Показано, что электрический импульс по мере своего движения по замкнутому меридиану сердца может «набегать» на периодический сигнал (R зубец) и накладываясь вызывать появление в сигнале ЭКГ Т зубца.
При создании образцов имитаторов работы сердца необходимо учитывать коэффициент замедления, т.к. реальные ткани миокарда отличаются по проводящим свойствам от металлов.
Инфаркт миокарда может быть вызван нарушением его топологии, т.к. в этом случае время «набегания» сокращается в два раза, что и приводит к совмещению R и Т зубцов.
Библиографическая ссылка
Арутюнова Е.Ю., Борщевская А.М. ВЛИЯНИЕ ТОПОЛОГИИ МИОКАРДА НА ФОРМИРОВАНИЕ Т ЗУБЦА В ЭКГ // Старт в науке. 2019. № 4-4. ;URL: https://science-start.ru/ru/article/view?id=1763 (дата обращения: 04.02.2026).
