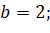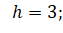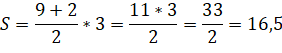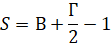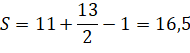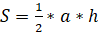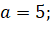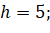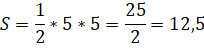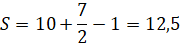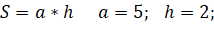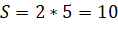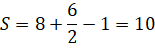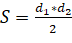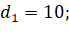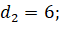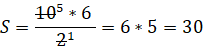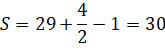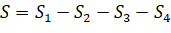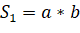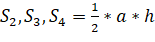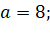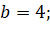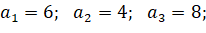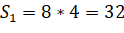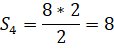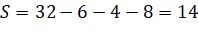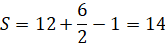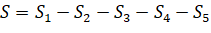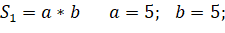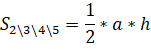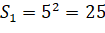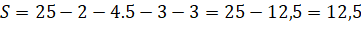1. Введение

Что такое математика? Это, конечно же, расчеты. Воплощение математических расчётов можно увидеть почти везде: в велосипеде, в автомобиле, в построенном здании, в телефоне. Всё это работает благодаря тому, что все данные объектов и их работы рассчитаны заранее по различным формулам. Кто-то над этим даже не задумывается, а кто-то увлеченно начинает вникать в расчёты на уроках математики. Часто это увлечение возникает при решении задач. Так, при изучении темы «Площади многоугольников» у меня возник вопрос: «Существуют ли задачи, которые отличаются от данных в учебнике?». Мой учитель рассказал, что такие задачи есть. Это задачи на клетчатой бумаге.

Клетчатая бумага привычна нашему глазу: мы пишем на уроках математики именно в таких тетрадях. Кто-то на ней рисует, кто-то чертит. А ведь именно клетчатая бумага является примером точечной решетки на плоскости. Задачи на клеточной бумаге разнообразны: можно вычислить площадь многоугольника, решить задачи на дроби и проценты.

Для многих задач на бумаге в клетку нет общего правила решения, что позволяет не просто выучить и зазубрить материал, а развивать умение думать, анализировать и размышлять. При изучении задач на клетке я выяснил, что существует теорема Пика. В школьной программе не изучается, но которая поможет мне быстрее справиться с заданием.

Объект исследования: формула Пика

Предмет исследования: методы и приёмы решения задач на вычисление площади многоугольника на клетчатой бумаге.

Гипотеза: площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формулам площадей.

Цель: выяснение существования другой, отличной от школьной программы, формулы нахождения площади многоугольника.

Задачи:

1. Найти различные методы и приёмы решения задач на клетчатой бумаге.

2. Проанализировать и систематизировать полученную информацию.

Ожидаемый результат: научиться использовать формулу Пика, которую можно применить в следующем учебном году на ОГЭ.

2. Кто такой Пик

Георг Алекса́ндр Пик — австрийский математик. До одиннадцати лет Георг получал образование дома (с ним занимался отец), а затем поступил сразу в четвёртый класс гимназии. В шестнадцать лет Пик сдал выпускные экзамены и поступил в университет в Вене. Уже в следующем году Пик опубликовал свою первую работу по математике. После окончания университета в 1879 году он получил право преподавать математику и физику. В 1880 году Пик защитил докторскую диссертацию, а в 1881 году получил место ассистента на кафедре физики Пражского университета. В 1888 году он был назначен экстраординарным профессором математики, затем в 1892 году в Немецком университете в Праге был назначен ординарным профессором (полным профессором).

Круг математических интересов Георга Пика был чрезвычайно широк: 67 его работ посвящены многим темам, таким как линейная алгебра, интегральное исчисление, функциональный анализ, геометрия. Но больше всего он известен своей формулой о вычислении площади многоугольника, которая появилась в его восьмистраничной работе 1899 года.

Эта формула оставалась незамеченной в течение некоторого времени, однако в 1949 году польский математик Гуго Штейнгауз включил теорему в свой знаменитый «Математический калейдоскоп». С этого времени формула Пика стала широко известна. В Германии формула Пика включена в школьные учебники [1].

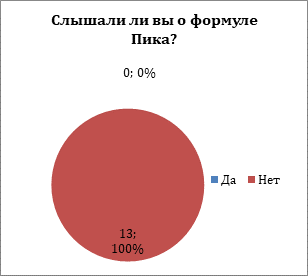
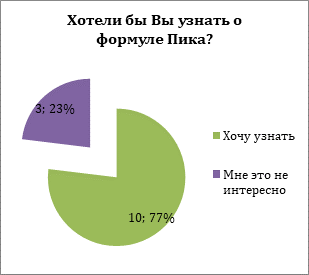
У нас в России эта теорема не включена в школьную программу. Я не слышал об этой формуле. А слышали ли о ней мои одноклассники...

3. Формула Пика

Каждый из нас хотя бы один раз сталкивался с расчетом площади многоугольника. В основном, это делают ещё по известным со школы формулам. Но в этом случае для каждой фигуры приходится помнить выражение её площади. Не легче ли использовать одну формулу для всех многоугольников?

Это формула Пика. Названа она в честь Георга Пика.

Запись формулы: S = В + Г / 2 − 1

S — площадь многоугольника.

В — количество целочисленных точек внутри многоугольника.

Г — количество целочисленных точек на границе многоугольника.

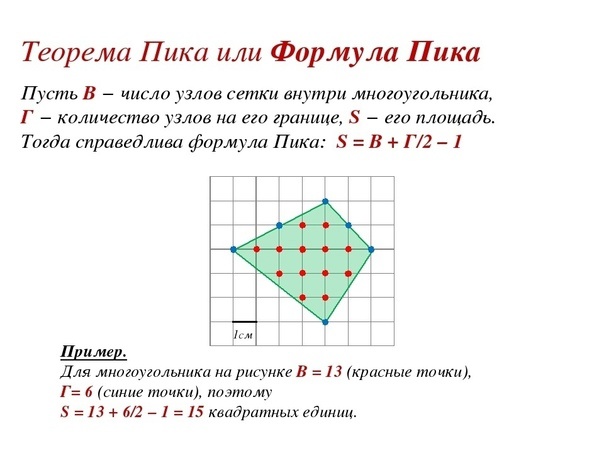
Важное замечание: формула справедлива только для многоугольников, у которых вершины расположены в узлах решетки клетчатой бумаги.

4. Стандартный способ нахождения площади многоугольника

В учебнике [2, с. 118], по которому я учусь, написано, что расчет площади по формулам основан на свойствах площадей.

Если два многоугольника равны, то единица измерения площадей и её части укладываются в таких многоугольниках одинаковое число раз, т.е. имеет место следующее свойство:

1. Равные многоугольники имеют равные площади.

Далее, пусть многоугольник составлен из нескольких многоугольников так, что внутренние области любых двух из этих многоугольников не имеют общих точек. Очевидно, величина части плоскости, занимаемой всем многоугольником, является суммой величин тех частей плоскости, которые занимают составляющие его многоугольники.

Итак:

2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Свойства 1 и 2 называют основными свойствами площадей. Напомним, что аналогичными свойствами обладают длины отрезков.

Наряду с этими свойствами нам понадобится еще одно свойство площадей.

3. Площадь квадрата равна квадрату его стороны.

Краткую формулировку этого свойства следует понимать так: если сторона квадрата при выбранной единице измерения отрезков выражается числом a, то площадь этого квадрата выражается числом a2.

Получается, что существует много разных способов решения задач на нахождение площади.

5. Эксперимент

Мной был проведен эксперимент в 8 классе, во время которого две группы одновременно решали одинаковые задание по вычислению площадей [3], но разными способами.

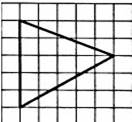
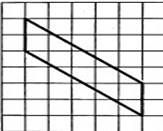
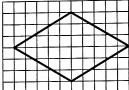
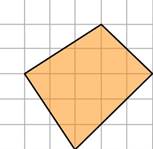
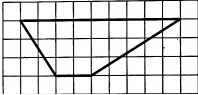
1.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Традиционное решение. ;
Решение с помощью формулы Пика.
2. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Традиционное решение.
Решение с помощью формулы Пика.
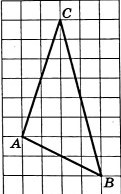
3. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Традиционное решение.
Решение с помощью формулы Пика.
4. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Традиционное решение.
Решение с помощью формулы Пика.
5. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Традиционное решение.
Решение с помощью формулы Пика.
6. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Традиционное решение.
Решение с помощью формулы Пика.

Конечно же, формулы, данные в учебнике, нужны. Однако этот эксперимент показал кратное уменьшение времени на решение с применением формулы Пика.

Таким образом, при решении задач с помощью формулы Пика времени затрачивается гораздо меньше.

6. Формула Пика в обыденной жизни

Данную формулу можно использовать и в жизни. Можно, например, найти площадь земельного участка. Обратимся, к примеру, к земельному участку дома моей семьи. Поскольку для применения формулы необходима квадратная решётка, я изготовил палетку с ячейкой 1см x1см. Наложил палетку на план участка и приступил к измерению его площади. Вычислил количество узлов, попавших на границу (Г=15) и внутрь объекта (В=29). Применив формулу Пика, вычислил площадь, выраженную в квадратных единицах (ячейках палетки): S=35,5. Но это значение необходимо пересчитать, учитывая масштаб плана. План участка изображен с масштабом 1:650, это значит, что в 1 см на плане содержится 6,5 м реального расстояния на местности. Что касается площади, 1 кв см плана соответствует 6,5*6,5=42,25 м кв. территории. Таким образом, площадь участка равна 35,5×42,25=1499,8 кв. м.

Аналогично можно вычислять (приближённо) площади географических объектов: площадь озера, моря, пустыни с погрешностью, так как там не будет многоугольника.

7. Заключение

Итак, в результате исследовательской работы я узнал о решении задач на клетчатой бумаге. При выполнении работы были решены задачи на нахождение площади многоугольников. Применение формулы Пика позволяет сократить время на решение задач. Формула Пика очень удобна и проста в применении. Эта исследовательская работа может иметь продолжение: задачи на клетчатой бумаге разнообразны, методы и приёмы их решения тоже.