• Авторы
• Научный руководитель
• Файлы
• Литература

Бородина С.А. 1

---

1 г. Нефтеюганск , МБОУ «СОШ №13», 6 Б класс

Базыльникова О.Ю. (г. Нефтеюганск, МБОУ «СОШ №13»)

Киргинцева Л.В. (г. Нефтеюганск, МБОУ «СОШ №13»)

Статья в формате PDF

0 KB

1. Андерсен Г.Х. Снежная королева: Сказки и истории / Пер. с дат. А. и П. Ганзен. – М.: ЗАО «Издательский Дом ОНИКС» , 1999;

2. Большой энциклопедический словарь: В 2-х т. /Гл. ред. А. М. Прохоров. – М.: Сов. энциклопедия, 1991. Т.1. – 1991 – 863 с., ил., с. 822;

3. Идеографический словарь русского языка. М.: Издательство ЭТС. Баранов О.С.. 1995

4. Литература. 5 класс. Учеб. для общеобразовательных организаций. В 2-х частях под редакцией В.Ф. Чертова. – 5-е изд. – М.: Просвещение, 2015;

5. Математика. 5 класс. Учебник под редакцией А.Г. Мерзляк, В.П. Полонский. – 2016;

6. Словарь-справочник по педагогике/Авт. – сост. В.А.Мижериков; Под общ. Ред. П.И.Пидкасистого. – М.: ТЦ Сфера, 2004. – 448с., с.212.

Математика и литература –

Две ветви человеческой культуры,

Две книги из одной библиотеки,

Две песни из единой фонотеки.

Такие разные, как буква и число,

Неразделимые, как лодка и весло.

Что их роднит, объединяет в вечность?

Великой мысли дух и бесконечность!

Всем известно, что люди условно делятся на «физиков» и «лириков». Они воспринимают мир по-разному. Первые – рассудительно и рационально, вторые – образно и эмоционально. Поэтому на первый взгляд, может показаться, что математика и литература это два несовместимых предмета, которые не имеют ничего общего. Многие даже считают такое сочетание странным.

Однако часто в литературных произведениях можно встретить математические задачи, которые ставят перед читателями авторы. Как правило, никто не обращает на это внимание, считая такие задачи лишь дополнением к сюжету, фоном, не несущим смысловой нагрузки.

Практически все литературные произведения содержат в сюжете перемещение героев. Перемещение тесно связано с движением и расстоянием, имеющими непосредственное отношение к математике. Мне стало интересно, возможно ли совместить эти две «несовместимые» науки?

Цель исследования: выявить факты использования математических моделей перемещения в литературных произведениях (по программе 5 класса).

Объект исследования: литературные произведения из программы курса 5 класса.

Предмет исследования: математические модели перемещения.

В основу исследования была положена гипотеза, согласно которой в литературных произведениях герои перемещаются в соответствии с определенными математическими моделями.

Для достижения поставленной цели ставились и решались следующие задачи:

1. Изучить и проанализировать литературные произведения курса 5 класса, описывающие перемещение героев;
2. Определить значение понятий «перемещение», «модель» и «математическая модель перемещения»;
3. Выделить виды математических моделей перемещения.

Для решения поставленных задач и проверки выдвинутой гипотезы мы использовали теоретические (анализ литературных произведений, изучение справочной математической информации) и эмпирические (сравнение, моделирование) методы исследования.

Исследование проводилось в три взаимосвязанных этапа.

На первом этапе (1 четверть: сентябрь-ноябрь 2016 г.) происходило определение актуальности проблемы исследования; выявление объекта и предмета, цели и задач; разработка плана исследования; уточнение значения основных понятий.

На втором этапе (2, 3 четверть: ноябрь 2016 г. – апрель 2017 г.) изучение литературных произведений, анализ справочной математической литературы.

На третьем этапе (4 четверть: апрель 2017 г. – сентябрь 2018 г.) анализ и обобщение полученных данных, формулировка выводов исследования; оформление текста исследовательской работы.

Научная новизна исследования состоит в том, что:

• уточнено значение понятий «перемещение», «модель» и «математическая модель перемещения»;
• выявлены виды математических моделей перемещений;
• возможность использования полученного материала на уроках литературы и математики в 5-х классах.

Перемещения героев в сюжетах литературных произведений

В 5 классе, при изучении раздела «Литературная сказка» нам было предложено выполнить задание: «Подготовить презентацию одной из литературных сказок Ханса Кристиана Андерсена и включить в своё выступление чтение или пересказ одного из эпизодов».

Я выбрала всем известную сказку «Дюймовочка». Читая ее, я обратила внимание на то, что Дюймовочка совершила путешествие. Она жила в тюльпане. Потом её украла жаба. Затем похитил жук «…мимо летел майский жук, увидал девочку, обхватил ее за тонкую талию лапкой и унес на дерево»[1]. Через некоторое время «…он снова обхватил ее, слетел с дерева и посадил на ромашку…»[1]. Целое лето девочка прожила в лесу. Когда наступили холода «…бедняжка пришла к дверям полевой мыши»[1]. Много еще приключений пришлось пережить Дюймовочке, прежде чем она встретилась с эльфом и стала «его женой, царицей цветов».

Я обратила внимание, что Дюймовочка совершила долгое путешествие. Мне стало интересно, сколько времени она провела в пути. Перечитав сказку еще раз, я определила, что Дюймовочка путешествовала почти целый год. Интересно, задумывался ли об этом сам автор? Можно ли преодолеть описанные расстояния за указанный срок?

При дальнейшем чтении и изучении произведений на уроках литературы я стала отслеживать перемещения героев. Проанализировав произведения, совместно с учителем литературы, мы пришли к выводу, что большинство авторов описывают путешествия или перемещения героев. Результаты исследования мы занесли в таблицу.

Таким образом, перемещения героев встречаются в эпических произведениях: рассказах, сказках, повестях, романах. Рассмотрим более детально некоторые произведения, в которых описаны перемещения героев. Отобразим в таблицах пункты отправления и назначения, а также остановки в пути, если они имеются.

Таблица 1

Анализ литературных произведений курса 5 класса

Таблица 2

Перемещения в сказке Х.К. Андерсена «Снежная королева»

Таблица 3

Перемещения в повести Н.В. Гоголя «Ночь перед Рождеством»

Таблица 4

Перемещения в были Л.Н. Толстого «Кавказский пленник»

В рассказе А.П. Чехова «Мальчики» главные герои Володя Королёв и Чечевицын, впечатленные рассказами Томаса Майн Рида, Фенимора Купера, Жюля Верна решили отправиться в Калифорнию. Они продумали план путешествия. «— Сначала в Пермь... — тихо говорил Чечевицын... — оттуда в Тюмень... потом Томск... потом... потом... в Камчатку... Отсюда самоеды перевезут на лодках через Берингов пролив... Вот тебе и Америка... Тут много пушных зверей.

— А Калифорния? — спросил Володя.

— Калифорния ниже... Лишь бы в Америку попасть, а Калифорния не за горами».

Анализируя данные таблицы, можно сделать вывод о том, что в некоторых произведениях герои перемещаются от одного пункта до другого без остановок (повесть Н.В. Гоголя «Ночь перед Рождеством», быль Л.Н. Толстого «Кавказский пленник») и с остановками (сказка Х.К. Андерсена «Снежная королева», рассказ А.П. Чехова «Мальчики»).

Математическая модель перемещения

В ходе анализа литературных произведений мы пришли к выводу, что в сюжете большинства произведений авторы описывают перемещение героев в пространстве. Прежде чем мы приступим к моделированию перемещения героев, рассмотрим значение понятия «математическая модель перемещения».

Для этого обратимся к справочной литературе. В Большом энциклопедическом словаре отмечено, что «модель - любой образ, аналог какого-либо объекта, процесса или явления» [2]. Словарь-справочник по педагогике трактует модель как «схему, изображение или описание какого-либо явления или процесса в природе, обществе [6].

Анализ значения термина «перемещение» показал, что этот термин имеет различное толкование в различных науках. В соответствии с идеографическим словарем русского языка перемещение это – изменение положения в пространстве, движение в другое место [3]

Таким образом, получаем что модель перемещения это схема или изображение изменения положения в пространстве; математическая модель перемещения – геометрическая фигура, характеризующая изменение положения в пространстве.

Виды математических моделей перемещения

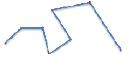
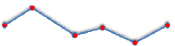
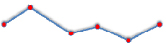
Также в ходе анализа перемещений героев в литературных произведениях нами было выявлено два типа перемещений: перемещение между двумя точками и перемещение между несколькими точками. В соответствии с обозначенными типами мы выделили два вида математических моделей перемещения: отрезок и незамкнутая ломаная. Связь математической модели перемещения и передвижения героев в литературных произведениях представлена в таблице.

Таким образом, все литературные произведения, описывающие передвижения героев можно разделить на две группы в соответствии с выделенными математическими моделями.

Таблица 5

Виды математических моделей перемещения

Заключение

В течение учебного года нами был проведен анализ литературных произведений, включенных в программу курса литературы 5 класса. В ходе анализа мы выявили, что большинство произведений содержат в сюжете перемещения героев.

Изучив значения понятий «перемещение» и «модель» мы сформулировали определение понятия «математическая модель перемещения». На основе классификации изученных геометрических фигур и проведенного анализа литературных произведений были выделены виды математических моделей перемещения.

Библиографическая ссылка