• Авторы
• Научный руководитель
• Файлы

Кирина Е.С. 1 Ткаченко Г.Р. 1

---

1 г. Калуга, МБОУ «Лицей № 9 имени К.Э. Циолковского», 7 «А» класс

Рылова И.Г. (Калуга, МБОУ «Лицей № 9 имени К.Э. Циолковского»)

Статья в формате PDF

0 KB

Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте II Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/2017/7/26982.

Прямая линия на плоскости – это одна из простейших геометрических фигур, знакомая вам ещё с младших классов, и сегодня мы узнаем, как с ней справляться с помощью математического анализа. Часто при изучении различных предметов, например, физики, (законы движения) требуется построить прямую; знать, каким уравнением задаётся прямая. Однако, часто построить прямую по заданной формуле линейной функции бывает затруднительно, если вычислять координаты точек прямой. Появилась гипотеза: уравнение прямой возможно задать не только по известной формуле y = kx + b.

Цель исследования: рассмотреть способы, с помощью которых можно составить уравнение прямой на плоскости и овладеть практическими навыками, техническими приёмами, которые потребуются для построения графиков линейной функции. Задачи исследования:

1. Ознакомиться с уравнением прямой с угловым коэффициентом.

2. Ознакомиться с общим уравнением прямой.

3. Ознакомиться с уравнением прямой в отрезках.

4. Научиться решать диафантовые уравнения 1 степени в целых числах.

5. Научиться строить прямую линию задаваемую формулой различными способами, переходя из одного вида уравнения прямой к другим. Выявить слабые и сильные стороны этих способов.

Теоретическая часть

Всем известный «школьный» вид уравнения прямой y = kx + b называется уравнением прямой с угловым коэффициентом k.

Общее уравнение прямой имеет вид:

Ax + By + C = 0,

где А, В, С – некоторые числа. При этом коэффициенты А, В, одновременно не равны нулю, так как уравнение теряет смысл.

В аналитической геометрии уравнение прямой почти всегда будет задано в общей форме. Ну, а при необходимости его легко привести к «школьному» виду с угловым коэффициентом y = kx + b (за исключением прямых, параллельных оси ординат).

Уравнение прямой в отрезках: если в общем уравнении прямой Ax + By + C = 0, С ? 0, то, разделив на –С, получим:

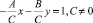или ,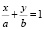

где

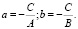
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ox, а b – координатой точки пересечения прямой с осью Oy.

Легко усмотреть, что данная прямая однозначно определяется красным и зелёным отрезками, отсюда и название – «уравнение прямой в отрезках».

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Диафантовые уравнения

Диофантовыми уравнениями называют алгебраические уравнения с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях должно быть не менее двух (если не ограничиваться только целыми числами). Диофантовы уравнения имеют, как правило, много решений, поэтому их называют неопределенными уравнениями. Диофантовы уравнения связаны с именем древнегреческого математика Диофанта Александрийского.

Правило 1. Если c не делится на d, то уравнение ax + by = c не имеет решений в целых числах НОД(a, b) = d.

Правило 2. Чтобы найти решение уравнения ax + by = c при взаимно-простых a и b, нужно сначала найти решение (X0, y0) уравнения ax + by = 1; числа CX0, Cy0 составляют решение уравнения ax + by = c.

Решить в целых числах (x; y) уравнение

5x – 8y = 19. (1)

Решение.

Первый способ. Нахождение частного решения методом подбора и запись общего решения.

Знаем, что если НОД(a, b) = 1, т.е. a; b взаимно-простые числа, то уравнение (1)

имеет решение в целых числах x; y НОД(5, 8) = 1. Методом подбора находим частное решение: X0 = 7, y0 = 2.

Итак, пара чисел (7; 2) – частное решение уравнения (1).

Значит, выполняется равенство:

5•7 –8•2 = 19. (2)

Вопрос: Как имея одно решение записать все остальные решения?

Вычтем из уравнения (1) равенство (2) и получим:

.

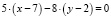Отсюда

.

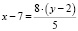Из полученного равенства видно, что число x – 7 будет целым тогда и только тогда, когда y – 2 делится на 5, т.е. 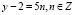. Итак, 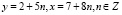, Тем самым все целые решения исходного уравнения можно записать в таком виде:

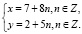
Второй способ. Решение уравнения относительно одного неизвестного.

Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент.

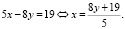
Остатки при делении на 5: 0, 1, 2, 3, 4. Подставим вместо y эти числа.

Если y = 0, то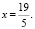

Если y = 1, то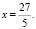

Если y = 2, то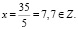

Если y = 3, то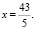

Если y = 4, то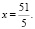

Итак, частным решением является пара (7; 2).

Тогда общее решение:

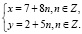
Третий способ. Универсальный способ поиска частного решения.

Для решения применим алгоритм Евклида. Мы знаем, что для любых двух натуральных чисел a; b, таких, что НОД(a, b) = 1 существуют целые числа x; y такие, что ax + by = 1.

План решения:

1. Сначала решим уравнение 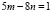используя алгоритм Евклида.

2. Затем найдем частное решение уравнения (1)по правилу 2.

3. Запишем общее решение данного уравнения (1).

1. Найдем представление: 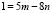. Для этого используем алгоритм Евклида.

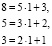
2. Из этого равенства выразим 1.

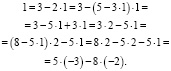
Итак, 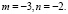Частное решение уравнения (1):

.

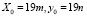Отсюда получим:

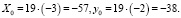
Пара 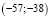– частное решение (1).

3. Общее решение уравнения (1):

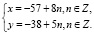
Четвертый способ. Геометрический.

План решения.

1. Решим уравнение 5x – 8y = 19 геометрически.

2. Запишем частное решение уравнения (1).

3. Запишем общее решение данного уравнения (1).

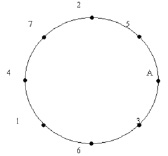
Отложим на окружности последовательно друг за другом равные дуги, составляющие 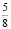-ю часть полной окружности. За 8 шагов получим все вершины правильного вписанного в окружность 8-угольника. При этом сделаем 5 полных оборотов.

На 5-ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли 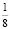-ю часть окружности, так что

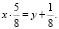
Итак, X0 = 5, y0 = 3 является частным решением уравнения 5x – 8y = 19.

2. Частное решение уравнения (1):

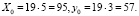
3. Общее решение уравнения (1):

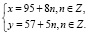
Практическая часть

ПРИМЕР 1.

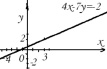
Построить график функции 4x – 7y = –2.

1 способ.

Определим две точки, принадлежащие графику данной функции, используя диафантовое уравнение: 4x – 7y = –2.

Легко подобрать частное решение: x = 3; y = 2.

Составим систему, которая определяет все целые решения:

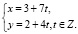
Задавая различные значения переменной t, получаем значения переменных x, y.

Например,

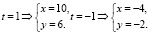
2 способ.

4x – 7y = –2. Выразим переменную х через y:

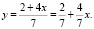
Нетрудно заметить, что трудно, занимает продолжительное время подобрать целое значение переменной x такое, чтобы значение переменной y также было целым. Значение переменной y будет принимать целое значение, если выражение 2 + 4x поделится на 7 без остатка, т.е.

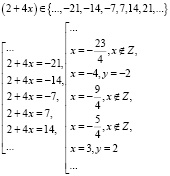
Строим график функции по двум найденным точкам (– 4; – 2), (3; 2).

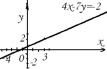
3 способ.

Найдем две точки графика функции 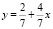, заполняя таблицу:

Сложно подобрать целое значение переменной x такое, чтобы значение переменной y также было целым.

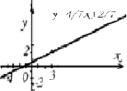
4 способ.

Преобразуем уравнение прямой 4x – 7y + 2 = 0 к уравнению прямой в отрезках:

.

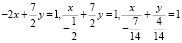Как видим, знаменатели дробей приведены к общему знаменателю для удобства построения прямой. За единицу масштаба выбираем 14 делений. Число 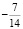откладываем на оси Ox, а число 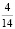на оси Oy:

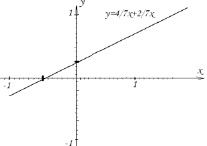
Способ рациональный, но создалась проблема с масштабной единицей.

5 способ.

Запишем функцию в особый вид: в числителе дроби должна стоять переменная x, если перед ней стоял знак «-», то его пишем в знаменателе дроби, содержащей переменную x, свободный член не преобразуем. В нашем случае функция примет вид:

.

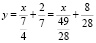На оси Oy откладывается число 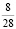, от него вправо вдоль оси Ox отступаем на 49 единиц, а затем вверх на 28 единиц вдоль оси Oy. Как видим, стоит проблема с масштабной единицей, поэтому построение таким способом затруднительно, но возможно.

6 способ. Построим график функции, используя точки пересечения с осями координат:

.

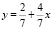Пересечение с осью Oy:

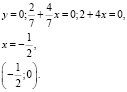
Пересечение с осью Ox:

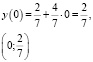
И вновь, видим, стоит проблема с масштабной единицей, поэтому построение таким способом затруднительно, но возможно. Данный способ приводит к уравнению прямой в отрезках.

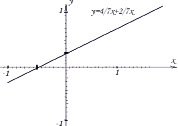
Итак, наиболее рациональными оказались 1 и 2 способы. Заметим, что функция, записанная с угловым коэффициентом, содержит дроби с одинаковыми знаменателями.

ПРИМЕР 2. Построить график функции

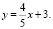
1 способ.

Определим две точки, принадлежащие графику данной функции, используя диафантовое уравнение: 4x – 5y = –15.

Легко подобрать частное решение: x = 0; y = 3.

Составим систему, которая определяет все целые решения:

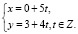
Задавая различные значения переменной t, получаем значения переменных x, y. Например,

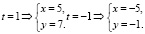
2 способ.

4x – 5y = –15. Выразим переменную y через x:

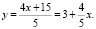
Нетрудно заметить, что трудно, занимает продолжительное время подобрать целое значение переменной x такое, чтобы значение переменной y также было целым. Значение переменной y будет принимать целое значение, если выражение 15 + 4х поделится на 5 без остатка, т.е.

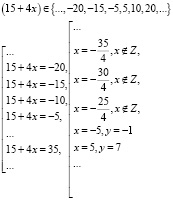
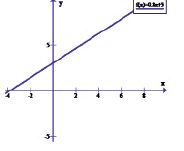
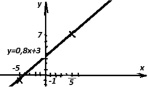
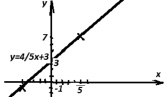
Строим график функции по двум найденным точкам (– 5; – 1), (5; 7).

3 способ.

Найдем две точки графика функции 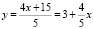, заполняя таблицу:

Необходимо подобрать целое значение переменной x такое, чтобы значение переменной y также было целым.

4 способ.

Преобразуем уравнение прямой 4x – 5y = –15 к уравнению прямой в отрезках:

.

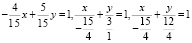Как видим, знаменатели дробей приведены к общему знаменателю для удобства построения прямой. За единицу масштаба выбираем 4 деления. Число 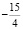откладываем на оси Оx, а число 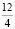на оси Оy:

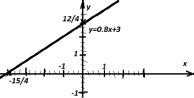
Способ рациональный, но создалась проблема с масштабной единицей.

5 способ.

Запишем функцию в особый вид: в числителе дроби должна стоять переменная x, если перед ней стоял знак «-», то его пишем в знаменателе дроби, содержащей переменную x, свободный член не преобразуем. В нашем случае функция примет вид:

.

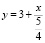На оси Оy откладывается число 3, от него вправо вдоль оси Оx отступаем на 5 единиц, а затем вверх на 4 единиц вдоль оси Оy:

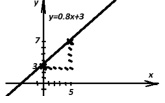
6 способ. Построим график функции, используя точки пересечения с осями координат:

.

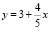Пересечение с осью Оy:

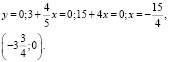
Пересечение с осью Оx:

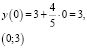
И вновь, видим, стоит проблема с масштабной единицей, поэтому построение таким способом затруднительно, но возможно.

Выводы

В школьном курсе алгебры построение графика линейной функции сводится к нахождению координат двух точек, так как её график – прямая. Легко построить прямую, если координаты полученных точек – целые числа. Однако, как показано выше, не всегда быстро можно подобрать такое значение аргумента, при котором и значение функции – целое число.

В ходе исследований способов построения прямой, прибегая к различным видам задания линейной функции, рассмотрены шесть способов, с помощью которых можно построить график линейной функции и овладеть практическими примерами, техническими приёмами, которые для этого потребуются. Осуществлён переход от нахождения целых решений линейного уравнения с двумя переменными к построению прямой в прямоугольной системе координат. Выбор того или иного способа зависит от сложности заданной формулы линейной функции, а умение сделать выбор – от приобретенных навыков и умений. Для построения графиков линейных функций пользовались программой Graph и программой Paint, а также комбинацией этих программ.

Библиографическая ссылка