Часто нам всем приходится видеть ДТП или даже быть участником ДТП.
Однажды, когда после школы шёл домой я видел как две машины столкнулись и одна машина вообще полностью перевернулась.
Там стояла патрульная служба и один человек из патрульной службы ходил и что-то измерял.
После этого мне стало интересно когда возникли первые правила дорожного движения, когда появились первые светофоры, и конечно же как математика связана с ДТП.
Цель: доказать что без математики бы не было всех правил дорожного движения и не смогли бы вывить нарушителя при ДТП.
Также провести своё исследование по ДТП.
Задачи: доказать что математика связана с ДТП. Познакомится со старыми светофорами, с первыми правилами дорожного движения и.т.д
Теоретическая часть
I. Немного истории. ОРУД- ГАИ ГИБДД
Проблемы безопасности движения появились задолго до изобретения машин. Гужевые повозки и пешие часто не могли разобраться, где кому ехать и идти, и как разъехаться встречным повозкам. Возчики лихо мчались по дорогам, нередко опрокидывая свои экипажи. А мешавших их движению пешеходов разгоняли кнутами.
Задолго до появления ОРУДа (отделы регулирования уличного движения) и ГАИ (государственная автомобильная инспекция) ещё в XVIII-XIX веках в царской России за движением конных экипажей осуществлялся полицейский надзор. Царь Петр I, императрицы Анна Иоанновна и Елизавета Петровна издали немало указов на этот счет.
Так в 1683г в России был издан именной указ, «сказанный разных чинов людям» царей Иоанна и Петра Алексеевичей: «Великим государям ведомо учинилось, - писалось в нем, - что многие начали ездить в санях на вожжах с бичами большими и, едучи по улице, небрежно людей побивают». Указ категорически запрещал управление лошадьми с помощью вожжей. Тогда считали, что, для того чтобы кучер лучше видел дорогу, он должен управлять лошадью сидя на ней верхом.
В 1812 г были введены правила, которые устанавливали: правостороннее движение, ограничение скорости, требование к техническому состоянию экипажей, введение номерных знаков для экипажей. Это были попытки организовать движение экипажей; систематических правил движения по улицам тогда не было. Пешеходное движение было беспорядочным и неорганизованным. Городовые с помощью жезла (короткая белая трость) и определенных приказом жестов стали регулировать дорожное движение. Когда же появились паровые, а затем и бензиновые автомобили, последовали и новые попытки, как в России, так и за рубежом, обеспечить безопасность движения.
Некоторые из них у нас сейчас могут вызвать лишь улыбку. Так, например, в Англии впереди парового экипажа должен был идти человек с красным флагом и предупреждать встречных о приближении паровика, а заодно усмирять перепуганных извозчичьих лошадей. Во Франции скорость движения бензиновых автомобилей в населенных пунктах не должна была превышать скорости пешехода. В Германии владелец машины должен был накануне заявить полиции, по какой дороге поедет «бензиновая тележка». В ночное же время езда на автомобиле вообще запрещалась. Если водителя в пути заставала ночь, он должен был остановиться и ждать утра.
Первое официально зарегистрированное дорожно-транспортное происшествие произошло в Великобритании 17 августа 1896 года. Автомобиль, который двигался со скоростью 6 км/ч, совершил наезд на пешехода. Сколько времени прошло с тех пор? (110 лет).
В те времена в России автомобилей было очень мало, поэтому вопросы безопасности ещё стояли не очень остро. Но шли годы, увеличивалось количество автомобилей, мотоциклов, велосипедов, трамваев и других транспортных средств. Вопросы создания условий безопасности движения властно просились на повестку дня.
После Октябрьской революции 1917 года охрана общественного порядка была отнесена в ведение Народного Комиссариата по внутренним делам (НКВД), вошедшего в состав Советского правительства – Совета Народных Комиссаров (СНК). 10 июля 1920 года Совет Народных Комиссаров принял указ «Об автодвижении по городу Москве и её окрестностям». Это были первые систематизированные правила движения. Они устанавливали предельные скорости движения: для легковых автомобилей – 25 верст в час, для грузовых – 15 верст в час. Не ограничивалась скорость для пожарных автомобилей. Запрещалась езда по левой стороне дороги и улиц, обгон на узких местах, срезание углов. Это был документ большого государственного значения. Он положил начало организации автомобильного движения в стране.
Регулирование транспортных и пешеходных потоков, надзор за соблюдением соответствующих правил стали во многих городах основными обязанностями постовых милиционеров. В их руках снова появился жезл, который имел красный цвет и желтую ручку.
В Ижевске первые, официально опубликованные Правила движения появились в 1925 году.
Через несколько лет участникам уличного движения стали подаваться сигналы с помощью переносных устройств семафорного типа.

В декабре 1930 года в Москве заработал первый трехцветный светофор. В городе Ижевске единственный подвесной светофор на перекрестке улиц М. Горького и Советская появился в 1958 году. Для его управления ежедневно из числа работников дорожного надзора выделялся сержант. Он забирался на высокую, похожую на трубу, будку, тумблерами включал или выключал тот или иной сигнал светофора. Второй светофор появился на перекрестке улиц Пушкинской и Удмуртской. Этот светофор был уже автоматическим. На ночь с 24 часов до 6 часов утра дежурные его выключали и ставили в режим желтого мигающего. В Москве 10 сентября 1931г., в составе управлений милиции были образованы отделы регулирования уличного движения (ОРУДы). Им в подчинение придавались строевые подразделения милиционеров – регулировщиков (отряды, дивизионы, взводы). Помимо надзора за соблюдением правил уличного движения милиции вменялась в обязанность их пропаганда среди населения, совершенствование организации дорожного движения, учет ДТП.
В декабре 1934 года в составе народного комиссариата Центрального управления шоссейных и грунтовых дорог и автомобильного транспорта была образована Государственная автомобильная инспекция (ГАИ).
Если ОРУДЫ в городах создавались и финансировались местными властями, то ГАИ представляла собой систему органов, содержащихся за счет средств госбюджета. Началась работа по созданию нормативной правовой основы деятельности ГАИ. В числе первых приказов были утверждены Правила по выдаче шоферских документов и учету шоферских кадров. Правила по учету автомобильного парка, инструкции о порядке производства ГАИ технических осмотров автомашин и прицепов. В 1939 году, после 10-летнего перерыва, регулировщики уличного движения вновь стали пользоваться жезлом, окрашенным в черно-белый цвет.
Несмотря на образование специальной службы (ГАИ), единых Правил движения по улицам и дорогам в стране по-прежнему не существовало.
Лишь с 1 января 1961 года были введены в действие первые единые для всей территории Советского Союза «Правила движения по улицам и дорогам Союза ССР». Сколько лет существуют эти единые правила? (46 лет).
С каждым годом увеличивался автомобильный парк, росла интенсивность движения на дорогах. Принимались все новые законы для регулирования движения транспортных средств. С развитием технического прогресса, возник вопрос: «Может ли ЭВМ помочь регулировать движение транспортных и пешеходных потоков?» Оказывается, может. Первая ЭВМ была использована для регулирования движения, а точнее работы светофоров, в 1959 году в канадском городе Торонто. С 1974 года и в России действует система координированного управления движения. Система чётко реагирует на изменения интенсивности движения по всей магистрали и изменяет время горения зеленых сигналов светофоров, отдавая преимущество наиболее загруженному направлению. Но человек также не остается сторонним наблюдателем. Он через мониторы следит за складывающейся ситуацией на перекрестках и всегда готов взять управление в свои руки. За электронно-вычислительной техникой большое будущее в регулировании дорожного движения.
С расширением функций ГАИ, название Госавтоинспекции не в полном объеме отражала все задачи и обязанности, возложенные на эту организацию и 15 июля 1998 года указом президента РФ Госавтоинспекция (ГАИ) была переименована в Государственную инспекцию безопасности дорожного движения МВД Российской Федерации (ГИББД).
II. Математика при расследовании дорожно-транспортных происшествий
1. Законы транспортного потока.
С каждым годом увеличивается количество транспорта на дорогах. Мы настолько привыкли к машинам, что порой забываем, что это источник повышенной опасности. Движутся в тротуарных руслах автомобили разных марок, автобусы, мотоциклы, велосипеды. Всё это называется транспортным потоком.
Почему в городах с плотными транспортными потоками ограничена скорость движения? Причина в том, что сначала с увеличением скорости интенсивность движения растет. Но так происходит до значений скорости 50-70 км/ч. Затем интенсивность начинает падать, потому что продолжает увеличиваться дистанция между транспортными средствами. Вот почему в городах и населенных пунктах скорость движения ограничивают до 60 км/ч, что соответствует обеспечению максимального пропуска транспорта по существующим дорогам.
Вычислить эту оптимальную скорость движения помогают законы математики (пропорции). Средняя скорость движения потока прямо пропорциональна интенсивности движения (количество транспортных средств, проходящих через сечение дороги за единицу времени) и обратно пропорциональна плотности потока (количество транспортных средств на единицу длины дороги, обычно 1 км).
Наверное, у каждого из нас когда-то возникал вопрос – почему дорога сделана именно такой ширины, а не другой? Этот параметр один из самых важных, так как именно он несет ответственность за пропускную способность дороги. И здесь математика помогает нам решить этот вопрос. Ширина проезжей части принимается такой, чтобы обеспечить пропуск максимального транспортного потока, который следует в часы пик по данному маршруту.
2.Первичныематериалы, собираемые для расследования ДТП.
Превышение скорости – это самое частое нарушение, которое приводит к дорожно-транспортным происшествиям. Каждое ДТП имеет свои особенности и для их дальнейшего расследования требуется четко установить конкретные первичные исходные данные, большая часть которых собирается бригадой ГИБДД, выезжающей на место ДТП непосредственно по факту и времени совершения событий, и фиксируется в документах. Инспектора, проводящие расследование, используют эти данные из протоколов проверки и осмотра технического состояния транспорта, протокола осмотра и схемы места ДТП, справки о ДТП.
Характеристика места ДТП включает в себя следующие данные.
Характеристика проезжей части: тип, состояние покрытия, план и профиль дороги на участке ДТП, ширина проезжей части, характеристика видимости дороги и объекта, создавшего опасность.
Например, асфальтобетон мелкошероховатый, мокрый; дорога прямая, уклон – 10% на подъем; видимость дороги с рабочего места водителя более 300м. Ширина проезжей части – 9,6 м для движения в одном направлении.
Практическая часть
В один из зимних дней я вместе с папой ехал на машине домой.
Впереди нас ехала машина она резко остановилась на светофоре, и мы тоже остановились а та машина которая ехала позади нас не успела вовремя затормозить и к тому же ещё асфальт был покрыт небольшим слоем льда она врезалась в нашу машину. Вот так я стал участником аварии. Я решил полностью расследовать эту аварию с помощью математики.
Замечание: скорость автомобиля по городу не должна превышать 60 км/ч.
Таблица 1
Таблица по ДТП
|
№ автомобиля |
Скорость |
Длина торможение автомобиля на ледяном покрытии |
Время торможения Автомобиля на ледяной поверхности |
|
1 автомобиль |
V?15км/ч |
7-8м |
2.8с |
|
2 Автомобиль |
V?10км/ч |
3-4 м |
3.25с |
|
3 автомобиль |
V?10км/ч |
4-5 м |
10-12с |
Вывод: водитель № 1 был не осторожен на дороге. 1) Была дорога покрытая льдом. 2) За 5-10метров был светофор.
Если бы он ехал с осторожностью и сбавив скорость то авария бы не произошла.
Таблица 2
Количество ДТП за 2015 год
|
ДТП |
Количество ДТП |
Погибли |
Получили травму |
|
Наезд на пешеходов |
345 |
10 |
347 |
|
Столкновения автомобилей |
132 |
6 |
186 |
|
Наезды на стоящие транспортное средство |
9 |
0 |
11 |
|
Опрокидывание |
7 |
1 |
9 |
Таблица 3
Количество ДТП за 7 месяцев 2016 года
|
ДТП |
|||
|
Наезд на пешеходов |
204 |
8 |
256 |
|
Столкновение автомобилей |
127 |
7 |
143 |
|
Наезды на стоящие транспортное средство |
10 |
1 |
9 |
|
Опрокидывание |
8 |
2 |
8 |
В 2016 году за семь месяцев произошло ПДД 204+127+10+8=349
В 2015 году за 12 месяцев произошло ПДД 345+132+9+7=493
|
За один месяц |
Количество |
|
2015 год |
?41 |
|
2016 год за семь месяцев |
?49 |
Задачи на ДТП и ПДД
1) Автомобиль, движущийся со скоростью 36 км/ч, должен на протяжении 155м находиться за осевой линией, чтобы объехать неисправный грузовой автомобиль. Сколько времени пройдет, прежде чем легковой автомобиль вернется на свою полосу движения?
Решение:
36км/ч=360*1000/3600=10м/с
t=S/V=155:10м/c=15.5с
Ответ: водителю автомобиля потребуется 15,5с
2) Если скорость велосипедиста, находящегося на дороге в 50м от перекрестка, равно 25 км/ч, то каким временем располагается водитель транспортного средства для пересечения этой дороги без риска наезда?
Решение
25км/ч=6,9м/с
t=S/V=50:6,9=7,2с.
Ответ 7,2 секундами располагается водитель транспортного средства чтобы пересечь эту дорогу без риска.
Математика при расследовании дорожно-транспортных происшествий
1. Законы транспортного потока. С каждым годом увеличивается количество транспорта на дорогах. Мы настолько привыкли к машинам, что порой забываем, что это источник повышенной опасности. Движутся в тротуарных руслах автомобили разных марок, автобусы, мотоциклы, велосипеды. Всё это называется транспортным потоком. Почему в городах с плотными транспортными потоками ограничена скорость движения? Причина в том, что сначала с увеличением скорости интенсивность движения растет. Но так происходит до значений скорости 50-70 км/ч. Затем интенсивность начинает падать, потому что продолжает увеличиваться дистанция между транспортными средствами. Вот почему в городах и населенных пунктах скорость движения ограничивают до 60 км/ч, что соответствует обеспечению максимального пропуска транспорта по существующим дорогам. Вычислить эту оптимальную скорость движения помогают законы математики (пропорции). Средняя скорость движения потока прямо пропорциональна интенсивности движения (количество транспортных средств, проходящих через сечение дороги за единицу времени) и обратно пропорциональна плотности потока (количество транспортных средств на единицу длины дороги, обычно 1 км). Наверное, у каждого из нас когда-то возникал вопрос – почему дорога сделана именно такой ширины, а не другой? Этот параметр один из самых важных, так как именно он несет ответственность за пропускную способность дороги. И здесь математика помогает нам решить этот вопрос. Ширина проезжей части принимается такой,10 чтобы обеспечить пропуск максимального транспортного потока, который следует в часы пик по данному маршруту.
2. Первичные материалы, собираемые для расследования ДТП Превышение скорости – это самое частое нарушение, которое приводит к дорожно-транспортным происшествиям. Каждое ДТП имеет свои особенности и для их дальнейшего расследования требуется четко установить конкретные первичные исходные данные, большая часть которых собирается бригадой ГИБДД, выезжающей на место ДТП непосредственно по факту и времени совершения событий, и фиксируется в документах. Инспектора, проводящие расследование, используют эти данные из протоколов проверки и осмотра порта, протокола осмотра и схемы места ДТП, справки о ДТП. Характеристика места ДТП включает в себя следующие данные. Характеристика проезжей части: тип, состояние покрытия, план и профиль дороги на участке ДТП, ширина проезжей части, характеристика видимости дороги и объекта,создавшего опасность. Например, асфальтобетон мелкошероховатый, мокрый; дорога прямая, уклон – 10% на подъем; видимость дороги с рабочего места водителя более 300м. Ширина проезжей части – 9,6 м для движения в одном направлении. Работники ГИБДД опрашивают свидетелей происшествия, проводят замеры необходимые для дальнейших математических вычислений и выяснения виновника ДТП. Именно за этими действиями инспекторов ГИБДД мы с одноклассниками наблюдали в тот роковой сентябрьский день.11
3. Доказательство уравнений, относящихся к скорости и их использование. С такими понятиями как перемещение, путь, скорость перемещения, скорость движения, постоянная скорость мы уже познакомились на уроках математики. Эти понятия нужны и инспекторам ГИБДД при расследовании дорожно-транспортных происшествий. Давайте вспомним эти термины и посмотрим, как применяются они при расследовании аварий. Перемещение. Положим, транспортное средство переместилось из точки А в точку В. Перемещение транспортного средства измеряется отрезком прямой, соединяющим указанные точки. Оно является вектором, так как характеризуется величиной и направлением, и всегда должно рассматриваться в направлении от начальной точки А до конечной точки В. Путь. В отличие от перемещения пройденный путь измеряется вдоль фактической траектории движения транспортного средства и является скалярной величиной. Перемещение и пройденный путь совпадают только при движении по прямой. Скорость движения. Она определяется как величина приращения пройденного пути за единицу времени. Она не зависит от направления движения и, следовательно, является скалярной величиной, имеющей только числовое значение. Средняя скорость равна отношению пройденного пути S к затраченному времени t: u=S/t. Скорость перемещения. Скорость перемещения определяется как величина приращения перемещения (в определённом направлении) за единицу времени и является, следовательно, векторной величиной, характеризующейся величиной и направлением.12 Пример. Если водитель проехал 13,3м в южном направлении за 1с, скорость перемещения составит 13,3м/c, или 48км/ч на юг. Скорость перемещения и скорость движения численно равны, если движение осуществляется по прямой. Постоянная скорость. Постоянная скорость перемещения имеет место в том случае, когда транспортное средство проходит равные отрезки пути за равные промежутки времени независимо от того, насколько малы эти промежутки. Если транспортное средство движется в данном направлении с постоянной скоростью 3м/c, то пройденный путь составит 3м в конце первой секунды, 6м в конце второй, 9м – третьей. Из этого следует, что объект, движущийся с постоянной скоростью u, за время t пройдет путь S=ut. Использование формулы S=ut. Наиболее часто эта формула используется для определения расстояния, пройденного за время реакции водителя. До того как водитель транспортного средства применит тормоза, он должен прореагировать на возникшую ситуацию. Если нет свидетельства в пользу иного, то в расчетах используется принятое в стране среднее общенациональное значение времени реакции 0,68с. Пример. Водитель едет со скоростью 45км/ч и замечает пешехода, сошедшего с пешеходной дорожки на проезжую часть. Какое расстояние автомобиль пройдет до принятия мер водителем по выходу из аварийной ситуации, если предположить, что его время реакции равно средней величине 0,68с? 45км/ч=12,5м/с. S=ut=12,5х0,68=8,5м Пример. Если пешеход переходит дорогу со скоростью 6,5 км/ч, какое расстояние он преодолеет за 2с? 6,5 км/ч=1,8м/с. S=ut=1,8х2=3,6м13 Использование формулы t=S/u. Пример. Если оценочное значение скорости велосипедиста, находящегося на дороге в 50м от перекрестка, равно 25 км/ч, то каким временем располагает водитель транспортного средства для пересечения этой дороги без риска наезда? 25км/ч=6,9м/с t=S/u=50:6,9=7,2с. Пример. Легковой автомобиль, движущийся со скоростью 20 км/ч, должен на протяжении 30м находиться за осевой линией, чтобы объехать неисправный грузовой автомобиль. Сколько времени пройдет, прежде чем легковой автомобиль вернется на свою полосу движения? 20км/ч=5,5м/с t=S/u=30:5,5=5,4с. Использование формулы u=S/t. Пример. Если транспортное средство преодолело 20м за 0,68с, то какова была скорость его перемещения? u=S/t=20:0,68=29,4м/c. 4. Практические примеры.
Пример 1
ДТП произошло в дневное время и заключалось в том, что на одну из двух женщин-пешеходов, переходящих дорогу со скоростным движением. Был совершен наезд транспортного средства слева. Оставшаяся невредимой спутница была способна исходя из особенностей планировки дороги, указать точное местонахождение приближающегося транспортного средства в момент начала их перехода через проезжую часть. После того, как свидетельница закончила переход дороги, она услышала удар от наезда транспортного средства на человека (рис.1).14 Анализ. Средняя скорость пострадавшей составляла, как выяснено, 5,5км/ч. Её в дальнейшем попросили пройти определенное расстояние в таком же темпе, как и при ДТП. Пройденное при эксперименте расстояние S=6м. Время ходьбы t=3,9c. Использована формула u=S/t. u =6:3,9=1,54м/с. Проезжая часть дороги имела ширину 7,3м, время перехода вычислено по формуле t=S/u, t=7,3:1,54=4,7с. Поскольку расстояние, пройденное автомобилем, и время проезда известны, можно определить и скорость. Расстояние S=173,1м; u=173,1:4,7=36,83м/с=132,6км/ч. Средняя скорость приближающегося транспортного средства может служить полезным ориентиром в расследовании ДТП, а в отсутствие других доказательств её роль ещё более возрастает. Если появится какое-либо новое свидетельство о скорости транспортного средства, то вычисление, пободное приведенному в данном примере, поможет подтвердить правильность или убедиться в ложности этого свидетельства. С другой стороны такое вычисление может показать, что пешеходы не проявили невнимательности при переходе проезжей части перед приближающимся транспортным средство
Пример 2
Совершен наезд легкового автомобиля на 14-летнего велосипедиста. Велосипедист выехал на главную дорогу с поворотом направо, автомобиль приближался к пересечению по главной дороге справа. Пострадавший ехал вслед за другим велосипедистом, также 14-летним, который остался невредимым. Водитель легкового автомобиля утверждала, что она увидела второго велосипедиста, выезжавшего на дорогу, когда она находилась на расстоянии 60м от точки наезда, и пока осознала15 происходящее, время на торможение не осталось. Скорость её автомобиля была 70 до 80 км/ч. Однако велосипедист, выехавший на дорогу первым, заявил, что, как он полагает, легковой автомобиль находился в 18м от точки наезда, когда второй велосипедист начал выезжать на главную дорогу. Расстояние, отсчитываемое по траектории движения велосипедиста от края дорого до точки наезда – 2,4м (рис.2). Анализ. Время проезда автомобилем расстояния 60м на скорости 80км/ч=22,2м/c t=S/u t=60:22,2=2,7с. Велосипедист не останавливался у края главной дороги, а выехал на неё с постоянной скоростью: u=S/t u=2,4:2,7=0,88м/с=3км/ч. Ясно, что скорость велосипедиста 3км/ч нереальна. Более вероятное значение скорости от 11 до 16 км/ч. Расстояние, которое велосипедист мог преодолеть за 2,7с при скорости 11км/ч (3м/с), S=ut; S=3х2,7=8м. Это расстояние 8м не соответствует утверждению водителя автомобиля. Время, требуемое для проезда 2,4м при скорости 11км/ч (3м/с), t=S/u; t=2,4:3=0,8с. Расстояние, пройденное автомобилем за это время при скорости 80км/ч (22,2м/с), S=ut; S=22,2х0,8=17,76м. Дальнейший опрос первого велосипедиста позволил определить, что в момент наезда он находился на расстоянии 8-9м от точки, где он выехал на главную дорогу. Отсюда следует, что велосипедист, которого водитель автомобиля видела въезжающим на главную дорогу, был первый велосипедист. Расстояние от точки наезда, соответствующее промежутку времени 0,8с, полностью согласуется с показаниями не пострадавшего велосипедиста и может в какой-то степени пояснить, почему водитель автомобиля не имела времени прореагировать на возникшую ситуацию.
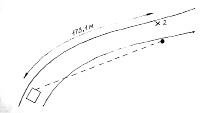
Рис.1. Схема к примеру 1. 1 – линия видимости пешеходом приближающегося легкового автомобиля; 2 – точка наезда.
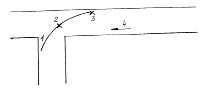
Рис.2. Схема к примеру 2. 1 – траектория движения велосипедистов; 2 – точка наезда автомобиля на второго велосипедиста; 3 – положение первого велосипедиста; 4 – направление движения легкового автомобиля
Вывод: в ходе проделанной мною работой, я смог определить, что количество ДТП в 2016 году возросло по сравнению с 2015 годам. Я проанализировал аварию с помощью математики в зимнее время года. Решил две задачи на ДТП и ПДД. Узнал много новой информации, она мне пригодиться в дальнейшем.
Библиографическая ссылка
Петров Д.В. МАТЕМАТИКА ПРИ РАССЛЕДОВАНИЕ ДТП // Старт в науке. 2016. № 4. ;URL: https://science-start.ru/ru/article/view?id=379 (дата обращения: 05.02.2026).
