Введение
Актуальность темы. Задача определения центра масс вызывала интерес среди ученых, начиная с III в. до н.э. Мыслитель Архимед, оперируя понятием центра масс, обнаружил возможность доказывать на его основе новые математические факты. Так, была установлена теорема о том, что три медианы треугольника пересекаются в одной точке. Позднее соображения Архимеда были использованы многими геометрами (Папп, Чева, Гюльден, Люилье и др.) [1-2]. Практическое применение метода расчета центра масс позволяет решать как теоретические задачи, так и реальные инженерные проблемы с высокой математической точностью [2-4].
Однако, следует отметить, что остаются не до конца изученными методы определения центра масс, в частности, речь идет об определении центра масс твердых тел, деформируемых тел, центра масс систем переменной массы. В связи с этим возникла актуальность проведения исследований в данном направлении.
Объектом исследования: метод геометрии масс.
Предмет исследования: практические методы расчёта центра масс сложной геометрической формы.
Цель работы: исследовать методы определения центра масс, определить наиболее оптимальные для расчёта устойчивости реальных объектов.
Гипотеза: применение математических методов расчета центра масс при решении олимпиадных задач.
Краткий обзор литературы
Понятие «центр масс» вводится в курсе геометрии 8 класса, в частности, для определения центра масс треугольника. Точка пересечения медиан треугольника – особая точка, которая в геометрии и в физике называется центром масс [2; 4].
Центр масс – это точка в пространстве, в которой можно считать сосредоточенной всю массу тела или системы тел для анализа их движения и поведения под воздействием внешних сил. В физике под материальной точкой понимают тело, размерами которого можно пренебречь при сравнении их с расстояниями до других тел, такое тело рассматривают как геометрическую точку.
В научных трудах М.Б.Балка и В.Г.Болтянского приведено следующее определение центра масс: такая точка, в которой сконцентрирована вся масса тела.
В книге [5, с. 71] говорится: «Центром тяжести некоторого тела является некоторая расположенная внутри него точка, обладающая тем свойством, что если за нее мысленно подвесить тяжелое тело, то оно остается в покое и сохраняет первоначальное положение».
Для наглядного формирования понятия центра масс, рассмотрим рисунок 1.
Персонаж на рисунке 1 в геометрическом смысле – многогранник. Предположим, что он состоит только из треугольников. Кроме того, многогранник должен не иметь самопересечений и ограничивать замкнутый объем, как и положено приличным многогранникам. Рисунок 1 (справа) некорректный, так как персонаж завалился вперед из-за смещения центра масс, который неверно рассчитан и вынесен за площадь опоры. Площадь опоры стоящего на поверхности многоугольника определяется как минимальный многоугольник, внутри которого окажутся все точки, находящиеся на поверхности. На рисунке 1 (слева) площадь опоры сдвинута под центр масс и больше (т.к. лапы динозавра больше), а на правой картинке сама площадь меньше и ближе к хвосту [6]. Исходя из определений выше и свойства центра масс, приходим к выводу, что данное понятие весьма распространенно в применении, как в начале III в., во время его открытия Архимедом, так и сейчас, в современном мире и требует дальнейшего изучения.
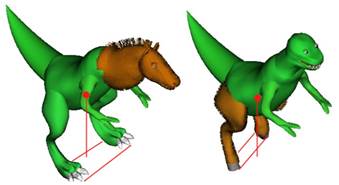
Рисунок 1 – Применение центра масс в компьютерном моделировании
Методы исследования
Методологическую и теоретическую основу проведенного исследования составляют современная теория геометрии масс, труды ведущих отечественных и зарубежных ученых, периодические издания по указанной теме, информация сети Internet.
В работе использованы следующие методы: сбор, анализ, синтез, сравнение, обобщение, систематизация информации, геометрические методы расчета центра масс.
ОСНОВНАЯ ЧАСТЬ
В XIX веке развитие теории механики позволило точно определить математические методы для вычисления центра масс различных систем тел.
Существует пять основных методов определения координат центра масс сложных тел и фигур: метод симметрии, метод разбиения, аналитический метод, барицентрический метод, экспериментальные методы (метод подвешивания, метод погружения, метод балансирования, метод вращения). Каждый из указанных методов применяется в зависимости от конкретных условий задачи и геометрических особенностей объекта.
Если однородное твёрдое тело имеет плоскость, ось или центр материальной симметрии, то его центр масс лежит соответственно или на плоскости симметрии, или на оси симметрии, или в центре симметрии. По этой причине центры масс однородного прямолинейного стержня, кольца, шара, поверхности сферы находятся в их геометрических центрах. Центры масс однородных прямоугольной и ромбовидной пластин находятся на пересечении их диагоналей. Центр тяжести однородной пластины в форме диска располагается в её геометрическом центре. Центр масс однородного тела, полученного вращением плоской кривой вокруг оси, лежащей в плоскости кривой и поверхности такого тела, находится на этой оси.
Положение центра масс тела сложной формы можно определить, если разбить его на конечное число таких частей, центры масс которых известны. Такой подход называется методом разбиения. Способ отрицательных площадей является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, полости, углубления, в которых нет массы.
Рассмотрим на практическом примере определение центра масс однородной пластины, изображенной на рисунке 2.
Поскольку фигура имеет вырезы, целесообразно применить метод отрицательных масс.
Площадь S пластины рассмотрим, как площадь фигуры, составленной из таких геометрических фигур: прямоугольник OABK с площадью S1, из которого вырезан квадрат MNPQ с площадью S2; прямоугольника KGEL с площадью S3, из которого вырезан полукруг радиуса a и площади S4; треугольника EFL с площадью S5. Центры масс каждой из частей обозначим, соответственно, 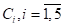 . Расчет относительно площадей и координат центров масс частей пластины сведем в таблицу 1.
. Расчет относительно площадей и координат центров масс частей пластины сведем в таблицу 1.
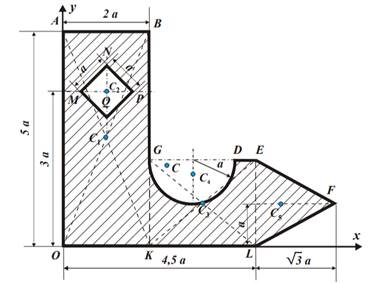
Рисунок 2 – Схема однородной пластины с размерами
Таблица 1
Расчет центра масс тела
|
№ части, i |
1 |
2 |
3 |
4 |
5 |
|
Si, м2 |
10 a2 = 0,4 |
a2 = 0,04 |
5a2 = 0,2 |
0,5π a2 ≈ 0,063 |
0,069 |
|
xCi , м |
a = 0,2 |
a = 0,2 |
4,25 a = 0,85 |
3a = 0,6 |
1,02 |
|
yCi , м |
2,5a = 0,5 |
3a = 0,6 |
a = 0,2 |
2a - |
0,2 |
Координаты центра масс рассчитаем по формуле стандартной для метода отрицательных масс:
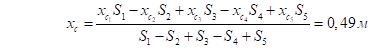
По аналогии рассчитаем координату y. Получим: ус = 0,38 м [8, стр. 20-21]. Центр масс указанной на рисунке однородной пластины, находится в точке (0,49; 0,38).
Пример приводит нас к выводу, что математически координаты центра масс определяются через статические моменты площади. Для плоской фигуры координаты вычисляются по формулам:
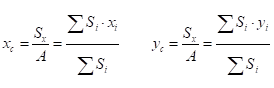 ,
,
где Sx, Sy – статические моменты относительно осей х и у, А – общая площадь фигуры.
Важно понимать, что центр тяжести не всегда располагается внутри самого тела. Например, у кольца или подковы центр тяжести находится вне материальной части объекта.
РЕЗУЛЬТАТЫ и ОБСУЖДЕНИЕ
Опираясь на анализ литературы, самым распространенным методом для вычисления центра масс объекта составной формы является метод разбиения или его модификации.
Однако, применить данный метод в исходном его виде для объекта трехмерной формы невозможно, так как расчет уже должен касаться трехмерного пространства, соответственно, добавляется третья ось – z, а вычислительная формула, относительно площади объекта должна быть заменена на характеристику касательно объемной фигуры.
Для решения данной задачи барицентрический метод, основанный на принципе аддитивности будет незаменим.
Рассмотрим модель программируемого робота, представленного на рисунке 3. Полагаем, что робот – это составное тело, система, состоящая из нескольких частей различной формы и плотности. Для нахождения их центра масс используется принцип аддитивности: центр масс составного тела можно найти, рассматривая его как систему материальных точек, где каждая точка соответствует центру масс отдельной части с соответствующей массой. Определение центра масс для тела, которое можно разбить на n элементов, массы которых m1, m2 … mn, и если известны координаты центров масс этих элементов x1, x2 … xn, можно выполнить по формуле:
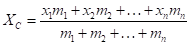 .
.
Аналогично будут рассчитываться координаты y, z.


Рисунок 3 – Модель программируемого робота
Согласно вышеизложенным замечаниям, разработаем алгоритм определения центра масс составных тел:
1. Разделить тело на части простой формы
2. Определить массу каждой части (если плотность однородна, масса пропорциональна объему).
3. Найти координаты центра масс каждой части.
4. Применить формулы для системы материальных точек.
5. При наличии полостей учесть их как части с отрицательной массой.
Также следует обращать внимание на особые случаи при работе с составными телами:
1. Тела с полостями:полость можно рассматривать как часть с отрицательной массой.
2. Тела с различной плотностью:необходимо учитывать различную плотность при расчете массы каждой части.
3. Тела сложной формы:для повышения точности можно разбить на большее количество простых элементов.
Следуя указанным формулам, провели расчеты и определили, что центр масс робота, указанного на рисунке 4, находится в точке С (4,5; 3,5; -3,5), расчеты выполнены относительно системы координат, представленной на рисунке 4 (слева от робота).
Информационные данные, полученные в процессе исследования могут быть применимы для решения олимпиадных задач.
Рассмотрим одну из них, которая была предложена школьникам на олимпиаде в Москве [9].
Робот движется по наклонной плоскости без проскальзывания (см. рисунок 4, а) угол наклона «Альфа» равен 30°. Центр масс робота находится в точке А, масса робота m1 = 1 кг . Расстояние от точки А до наклонной плоскости принять равным 0 м (эта величина называется «клиренс»). Высота робота АБ = 0,4 м. Колеса робота установлены, как показано на рисунке, симметрично прямой (АБ), расстояние между точками касания колёс В и Г с наклонной плоскостью равно ВГ =20 см. В верхней точке наклонной плоскости робот берёт груз массой m2 и укладывает его на себя, как показано на рисунке 4 (а). Центр масс всего груза находится в точке Б. Толщиной грузов по сравнению с АВ можно пренебречь. Определите максимальную массу «m2», при которой робот не начнёт опрокидываться.
Решение: для решения задачи трансформируем рисунок (4, б). Так как центр масс робота расположен в т.А, а центр масс груза расположен в т.Б, то центр масс робота с грузом располагается в т. М на прямой АБ. Если вертикальная линия, проведенная через центр тяжести М тела, пересекает площадь опоры, то тело находится в равновесии. Если же вертикальная линия, проведенная через центр тяжести, не пересекает площадь опоры, то тело опрокидывается. Рассмотрим граничный случай, когда проекция т. М. на ось ОХ совпадает с проекцией т. В на эту ось. Тогда, используя, формулу:
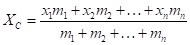
получаем: 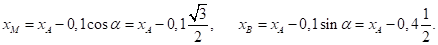
Подставим эти данные в исходное выражение и решим задачу:
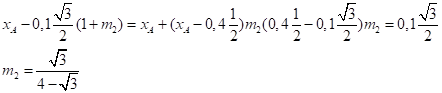
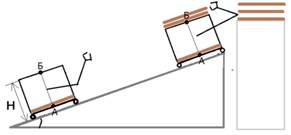
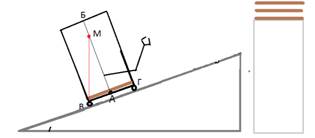
Рисунок 4 (а, б) – Иллюстрация к олимпиадной задаче
Рассмотренная выше задача была предложена для решения одноклассникам. Естественно, для решения первоначально ознакомили ребят с теоретическими сведениями по теме и формулами, которые нужно использовать в расчетах. Следует отметить, что из 26 человек, участвующих в тестировании задачи, с решением справились на 100% – 5 человек из класса, 15 человек – справились с небольшой помощью, остальные – не смогли решить задачу даже с подсказками.
ЗАКЛЮЧЕНИЕ
Определение центра масс – ключевой аспект проектирования и анализа физических систем с применением математических методов. В работе представлены различные вариации методов определения центра масс. Исходя из выполненных исследований, пришли к выводу, что умелое владение различными методами расчета, от математических формул до практических экспериментов, открывает возможность не только проектировщикам, инженерам, исследователям для решения широкого спектра задач, а в первую очередь, школьникам старших классов. Решение задач при помощи барицентрического и экспериментальных методов расширяет пространственное мышление учеников. Данные, полученные в таком формате, могут быть применимы не только в инженерных задачах, но и в задачах 3-Д моделирования, даже написании игр.
Сформулированная в начале работы гипотеза подтверждения опытным путем. Методы расчета центра масс, действительно, могут быть применимы для решения олимпиадных задач.
Библиографическая ссылка
Крыжановская Н.М. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ РАСЧЕТА ЦЕНТРА МАСС ОБЪЕКТОВ РАЗЛИЧНОЙ ФОРМЫ // Старт в науке. 2025. № 6. ;URL: https://science-start.ru/ru/article/view?id=2522 (дата обращения: 05.02.2026).

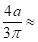 0,32
0,32