«Предмет математики настолько серьёзен,
что полезно не упустить случая,
сделать его немного занимательным»
Б. Паскаль

В своей деятельности человек повсюду сталкивается с такими геометрическими фигурами как треугольник, прямоугольник, круг и т.д.. Изобразить их на листе бумаги или мелом на доске не составит труда любому среднестатистическому школьнику. Но наша жизнь протекает не на плоскости, а в трехмерном измерении, где гораздо важнее иметь пространственное мышление и необходимость изучать форму, размеры, взаимное расположение пространственных фигур. С такими фигурами их свойствами и задачами школьники знакомятся в старших классах и сталкиваются со многими трудностями. Раздел геометрии, в котором изучаются такие тела и решают задачи, называется стереометрией (от греч. «стереос» - «объемный», «пространственный»). Поэтому выбор данный темы стал для нас наиболее актуален, так как чем раньше мы начнем знакомство с пространственными фигурами, будем знать их формы и происхождение от плоских фигур, тем легче получить знания в старших классах.

Цель, гипотеза и задачи проекта

Как правило, математика для многих сложная наука и привить к ней интерес задача любого учителя, поэтому на наш взгляд, если добавить немного волшебства и сказки, уроки станут более интересными. А если собрать из пространственных фигур различных героев, то любому учащемуся станет забавно и интересно этим заниматься.

Нами выдвинута гипотеза: чем больше мы будем уделять время интересным геометрическим задачам с использованием в них пространственных сказочных фигур, акцентируя внимание на их форму и создание, тем лучше будем знать все пространственные тела и их свойства.

Проведя анкетирование среди своих одноклассников, мы сделали вывод, что многие не сопоставляют, что коробочка – это параллелепипед, стакан – это приближенная форма цилиндра, т.е. то, что окружающие нас предметы геометрические тела и получаются они из плоских фигур.

Цель нашей работы: познакомить ребят с пространственными фигурами, научиться их распознавать и сделать это в игровой сказочной форме.

Достижение данной цели требует решение следующих задач:

1. Проанализировать учебную литературу и выявить геометрические фигуры в сказках и придумать к ним математические задачи.

2. Привести примеры сказочных задач по геометрии.

3. Сделать практическую работу по выполнению пространственных фигур.

4. Оформить в классе ознакомительный уголок пространственных фигур.

Для подтверждения нашей гипотезы, мы проводили эксперимент в 3 классе. Перед использованием сказочных задач и знакомства с истоками стереометрии мы провели тестирование, целью которого было - выявить знакомы ли школьники младших классов с пространственными фигурами. Вопросы были следующие:

1. Какую фигуру можно получить, вращая квадрат вокруг одной из его сторон?

2. Какую геометрическую форму имеет куриное яйцо?

3. Поставьте три пальца образовав треугольник и поднимайте их собирая в одну точку, как думаете какая фигура у вас получилась?

4. Представьте сказочный замок принцессы из каких пространственных фигур вы бы его составили?

5. Изобразите как вы представляете призму.

Отвечая на вопросы, большинство ребят представляли плоские фигуры и никак не могли их сделать объемными. Даже яйцо они писали многие круг, а не овал, и уж точно не эллипсоид, если быть точными в стереометрических понятиях. По экспериментальным данным мы получили следующую диаграмму владения понятиями.

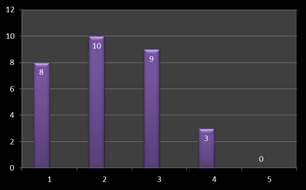
Рис. 1 – Результаты анкетирования

После нашего опроса, мы стали больше уделять внимание геометрическим объектам на уроках, и как уже было сказано выше, интерес к этому стал очень высоким с использованием сказочных задач.

Мир сказок с элементами геометрии

Все мы читали разные сказки, но никто не сопоставлял, что герои или главные действующие лица в них представляют собой геометрические тела. К примеру, всем известный колобок имеет форму шара; золотое яичко в «Курочке Ряба» эллипсоид; теремок – это соединение призмы и четырехугольной пирамиды. А ведь используя эти простые народные сказки легко можно показать геометрические фигуры в них.

При знакомстве с окружностью, мы предлагаем рассмотреть сказку «Репка», форма репки круг, сначала маленькая, потом выросла большая. Какое расстояние увеличилось? Подвести к понятию диаметра и радиуса окружности.

Рис. 2 Сферическое тело в окружающем мире

А в жизни все видели репку и она объемная, получаем из вращения окружности шар или сферу.

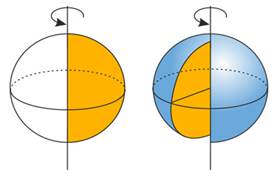
Рис. 3 – Сфера в вращении

Приведем примера нашего урока на тему: «Прямоугольник» с применением методики использования сказочных задач и представление пространственных фигур.

Начнем с сказки: Жили-были в чудесной стране Геометрии Карандаш и Линейка. Как-то раз задумали они начертить четырехугольник, у которого все углы – по 900. Чертили-чертили целый день. Особенно старалась Линейка. Она ложилась ровно, не наклоняясь. Карандаш отчетливо проводил и соединял линии. В конце концов у них получилась такая фигура. На радостях отправились они к своему другу Транспортиру. Он жил неподалеку от наших героев. Это был удивительно трудолюбивый и внимательный инструмент. Он напоминал половину круга, и поэтому его еще иногда ласково называли Пирожок. Пришли наши герои и попросили у него помощи:

– Послушай, Пирожок, помоги нам. Мы целый день чертили фигуру, у которой все углы должны быть по 90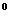. А так ли у нас получилось, мы не знаем. Проверь, пожалуйста.

А у Транспортира на спинке было много делений от 0 до 180. Проверка величины углов – его самое любимое занятие. Поэтому он, конечно, согласился. Все углы у четырехугольника действительно были равны 90. А потом он улыбнулся и сказал:

– Угол, равный 90, – это прямой угол, а четырехугольник, у которого все углы – по 90, называется прямоугольником. В следующий раз, когда соберетесь что-нибудь чертить, – сказал Транспортир, – не забудьте про меня. Я обязательно приду к вам на помощь, и дело быстрее сладится.

Так мы и узнали, что такое прямоугольник и как его нужно рисовать, о его свойствах и необходимых для этого инструментов.

Помимо того, что можно изобразить прямоугольник в тетради, отметить длины его сторон, мы уделяем внимание его движению в пространстве. Для этого вырезали из плотной бумаги прямоугольник зафиксировали рукой одну сторону и вращали его вокруг нее. Воображая пространственную фигуру и очень многие догадались, что получился цилиндр. А для закрепления этого следующая сказка:

Жили-были два друга Круг и Прямоугольник, дружно жили, весело. Особенно они любили лето, больше игр на свежем воздухе, свободного времени и всяких витаминов. В один жаркий день очень им захотелось искупаться, а водоема близ их жилья не было и решили они сами бассейн себе сделать. Думали, думали они как это сделать и решили пойти к местному мудрецу. Мудрец выслушал их, оглядел, подумал и сказал:

- С вашими формами грех бассейн не соорудить. Посмотрите внимательно на свои формы, примените их в постройке. Да будет прекрасный бассейн.

Вернулись друзья домой, посидели, рассмотрели себя, не догадывались они, что их геометрические формы помощники. Встал Прямоугольник на лужайке, да как начал крутиться вокруг своей боковой стороны. Смотрят они, а на лужайке круг образовался, не верят своим глазам, Круг даже прилег померил, форма подошла.

- Так это ж идеальное дно нашего бассейна!!! А если у тебя будет проволока, то по твоей высоте мы и бортики построим!!!

Так и сделали, получили отличный каркас бассейна, а уж из него специальными материалами сделали и сам бассейн.

Лежат, наслаждаются водой и солнышком, проходит мимо Мудрец.

- Смотрю справились вы с задачей, получили нужное решение, а название этой фигуры знаете какое? Цилиндр!!

Вот так если присмотреться к окружающим предметам, то во всем можно увидеть геометрические фигуры.

Сказочное превращение плоских фигур в объемные тела

Одной из главных задач нашей работы является знание объемных тел и их связи с плоскими геометрическими фигурами. Каждую фигуру мы рассмотрели, разобрали ее составляющие части – плоские фигуры. Вырезали их, вращали, собирали в объемные тела. Так же для наглядности мы решили оформить в классе уголок с такими муляжами, чтобы одноклассники видели - как выглядят стереометрические фигуры. Поэтому для каждой пространственной фигуры мы сделали свои модели.

1. Параллелепипед (куб). Получается из соединения 6 прямоугольников (квадратов). Легче всего использовать развертку данного типа.

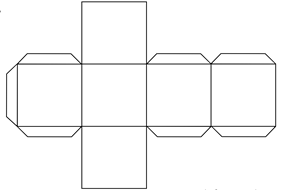
Рис. 4 – Развертка куба.

2. Цилиндр. Опыт его создания состоял в следующем: вырезаем из картона две одинаковые окружности, рисуем с помощью циркуля. По кругу с помощью иголки делаем дырочки на обоих кругах. Затем по количеству полученных отверстий заготавливаем равной длины столько ниток и скрепляем две окружности. Натянутые между окружностями нитки создают боковую поверхность цилиндра. Модель хороша тем, что можно показать разную высоту цилиндра, прямой и наклонный вид. Второй вид модели выполнили из бумаги: для этого была использована следующая развертка.

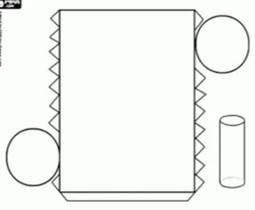
Рис. 5 – Развертка цилиндра.

3. Сфера (шар). Опыт его создания состоял в следующем, взяли воздушный шар, надули до определенного размера и обматывали нитками, проклеивая каждый слой. Сам надувной шар легко извлечь после полного высыхания. Так же вариант склеивать сферу по развертке, но на наш взгляд это сложнее.

4. Конус. Состоит из кругового сектора и окружности. Простейшей разверткой для его получения служит следующий макет.

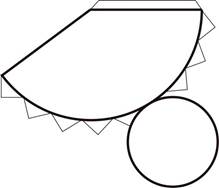
Рис. 6 – Развертка конуса.

5. Пирамида (тетраэдр). Пирамиды могут быть треугольные, четырехугольные, шестиугольные и т.д. Это зависит от фигуры, лежащей в основании пирамиды. Мы остановились на правильной треугольной пирамиде, она состоит из 4 равносторонних треугольников. Ее развертка имеет вид.

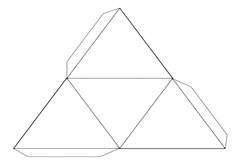
Рис. 7 – Развертка тетраэдра.

Практическая реализация проекта

Одной из главный задач нашей работы было создать уголок знакомства с стереометрическими телами, а также использовать их в качестве героев сказок.

Наша работа началась с изучения разверток каждой фигуры и построения ее чертежа. Далее аккуратно вырезали и склеивали детали. Получая модель за моделью. При работе с сферой нам нужны были нитки, клей и воздушный шарик. В течении двух недель мы работали над изготовлением моделей каждого вида геометрического тела.

После этого мы напечатали несколько плакатов, содержащих понятие стереометрии и рисунки всех геометрических тел с их наглядным представлением в жизни вокруг нас. Конечно же уделили внимание и, изучаемыми нами, плоским фигурам. Так у нас образовался в классе «Уголок знакомства с пространственными телами»

Рис.8- Уголок стереометрии

Ребята с вниманием и интересам изучали новый для них материал, название и формы стереометрических фигур. Затем мы провели практическое занятие по изготовлению понравившейся фигуры. Нашей задачей являлось привить интерес к пространственным фигурам и делали мы это, конечно же с помощью сказок. Представляя наши фигуры героями сказок, мы сочиняли для них имена и истории.

Заключение

В ходе нашей работы мы получили много положительных моментов на занимательных уроках. Ребята стали лучше разбираться в геометрических понятиях. Соединения геометрических фигур в пространственное тело вызвало интерес, теперь каждый мой одноклассник знает из какой фигуры можно получить пространственное тело и его правильное название. Попробовав смастерить фигуру самостоятельно, каждый развивал свое пространственное мышление. А использование стереометрических фигур как игрушек в театральной постановке вызвало много веселья и позитива.

Повторное тестирование по тем же вопросам, после применения данных методик, дало уже совершенно другие результаты. Это видно на диаграмме.

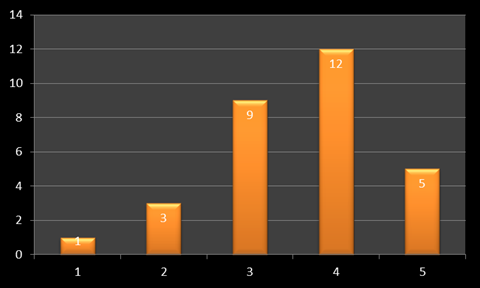
Рис.9 – Итоговое анкетирование.

Уже в ходе нашего эксперимента мы поняли, что данные занятия несут положительный результат, а итоговое анкетирование это подтвердило. Смело можем утверждать, что такой подход имеет огромный эффект в систематизации геометрических знаний и несет в себе пропедевтику изучения стереометрии в старших классах.