Введение
Моделирование в научных исследованиях применялось еще в глубокой древности. В настоящее время невозможно назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования.
Результатом любого моделирования является модель – прототип реального объекта, который дублирует его основные свойства, характеристики, создаваемый для реализации различных целей и используемый в разных отраслях [1]. Что же касается научных исследований, то модель создается, как правило, с целью замещения объекта-оригинала.
Математическое моделирование — частный случай моделирования. Является важнейшим видом знакового моделирования и осуществляется средствами языка математики [1, 2].
Актуальность выбранной темы обусловлена тем, что задача о загрузке (задача о рюкзаке) и различные её модификации широко применяются на практике в прикладной математике, криптографии, экономике, логистике, для нахождения решения оптимальной загрузки различных транспортных средств и пр. А для успешного решения поставленной задачи важно выбрать верный алгоритм её решения. В этом и есть рассматриваемая в работе проблематика. Либо выбирать быстрый алгоритм, либо точный.
Цель работы: исследовать алгоритмы решения классической задачи о рюкзаке. Протестировать их и сравнить по скорости решения, по точности. Определить, в каких случаях следует использовать тот или иной подход к решению задачи.
Объектом исследования выступают методы математического моделирования при решении задачи об оптимизации загрузки.
Предмет исследования – задача о рюкзаке в математическом моделировании.
Задачи исследования:
1. Изучить литературу по теме работы.
2. Исследовать методы математического моделирования при решении задачи об оптимизации загрузки.
3. Разработать собственную математическую модель по оптимальному планированию рациона питания школьника.
4. Реализовать практическое применение модели при помощи электронной таблицы MS Excel.
Гипотеза: математическое моделирование применимо не только при решении технических, экономических задач, но и задач бытового характера.
Методы исследования
Для реализации целей работы применялись следующие методы исследования:
- анализ литературы, научных работ;
- исследование алгоритмов решения классической задачи о рюкзаке;
- практическая реализация, тестирование разработанной модели;
- обобщенный анализ расчетов.
Основная часть
Одной из самых распространенных задач математического моделирования является задача об оптимальной загрузке рюкзака.
Задача о рюкзаке – одна из задач комбинаторной оптимизации. Классическая задача звучит следующим образом: имеется набор из N предметов, каждый предмет имеет массу 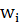 и полезность
и полезность 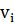 , i=(1,2..N), требуется собрать ранец с максимальной полезностью таким образом, чтобы он имел вес не больше W, где W – вместимость рюкзака. Полагают что
, i=(1,2..N), требуется собрать ранец с максимальной полезностью таким образом, чтобы он имел вес не больше W, где W – вместимость рюкзака. Полагают что 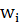 ,
, 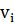 ,
, 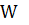 , P – целые неотрицательные числа [2].
, P – целые неотрицательные числа [2].
Алгоритмы решения задачи о рюкзаке можно разделить на приближенные и точные. Точные: применение динамического программирования, полный перебор, метод ветвей и границ (сокращение полного перебора). Приближенные алгоритмы: жадный алгоритм.
В процессе научных исследований был выполнен сравнительный анализ указанных выше алгоритмов и составлена аналитическая таблица (см. таблица 1).
Таблица 1 – Сравнительная характеристика методов решения задачи о рюкзаке
|
Название метода |
Принцип действия |
Достоинства |
Недостатки |
|
Полный перебор (вручную) |
перебор всех возможных вариантов |
Прост в понимании, использовании, дает точное решение |
Медленный, неэффективный. Сдобавлением каждого нового предмета число комбинаций удваивается, так что сложность такого алгоритма – 2n |
Жадный алгоритм |
накаждом шаге добавляем врюкзак самый дорогой предмет, пока лимит веса непревышен |
Простота и быстрота реализации. Может работать с большим количеством значений N |
Не точный, т.к. не учитывает значимости элемента, т.к. оценивает только его вес |
|
Метод ветвей |
построение графа |
Простота и наглядность реализации |
Работает также медленно, как и метод полного перебора |
|
Динамическое программирование |
разбивается на подзадачи. Оптимальное решение на шаге находится исходя из найденных оптимальных решений |
дает самое точное решение задачи, высокая скорость работы по сравнению со всеми остальными методами |
трудоемкие затраты, а также хранение большого объема промежуточных данных |
Данные таблицы 1 дают право судить о том, что наиболее эффективным методом решения задачи о рюкзаке является динамическое программирование. Докажем это на примере составления оптимального рациона сбалансированного питания школьника.
Анализируя проблемы современных школьников, опираясь на опыт психологов и исследователей данного направления, статистику детских заболеваний [3], используя собственные наблюдения, пришли к выводу, что главными критериями, влияющими на здоровое самочувствие, эффективность и успешность школьника являются: здоровый образ жизни, полноценный сон, сбалансированное питание.
Исследования в статье будут касаться критерия 3 – сбалансированное питание.
Учащимся ГБОУ «Свердловская специализированная школа» был предложен опрос на Яндексформ, содержащий 10 вопросов относительно видов питания. Анализ ответов показал, что 55 % школьников – «предпочитают быстрые перекусы, питаются «на ходу» в течении учебного дня», 30 % – «предпочитают «подкрепится» чипсами и газировкой», 15 % – «питаются полноценно, минимум три раза в день, как правило, дома и в школьной столовой во время посещения школы».
Следует отметить, что указанные данные говорят о несбалансированном питании школьников, которое влечет за собой ряд проблем: ухудшение самочувствия ребенка, снижение трудовой активности, как следствие – снижение уровня успеваемости. В большинстве случаев школьники просто не задумываются о том, что «быстрая и вкусная еда» не всегда полезна для организма.
С целью исключения указанной проблемы принято решение: разработать математическую модель для решения задачи оптимальной загрузки суточного рациона питания школьника.
Критерии (ограничения), которые необходимо учесть в математической модели: возрастные особенности; пол ребенка; физическая активность в течение дня; в рацион должны быть обязательно включены категории продуктов, указанных в п. 1, 2, 4, 6,8, указанных в таблице 2.
Таблица 2 – Категории продуктов питания, потребляемые школьниками в течение дня (MaxW = 2000 ккал)
|
№ п/п |
Категория продуктов, |
Вес, |
Эффективность (прибыль), |
|
1 |
Молочные |
75 |
26 |
|
2 |
Фрукты и овощи |
50 |
19 |
|
3 |
Конфеты, печенье, другие сладости |
500 |
10 |
|
4 |
Мясо, рыба, яйца, бобы |
300 |
25 |
|
5 |
Чипсы, фастфуд |
600 |
12 |
|
6 |
Хлебобулочные изделия, картофель, рис |
150 |
27 |
|
7 |
Соусы, майонезы, приправы |
200 |
13 |
|
8 |
Напитки |
20 |
8 |
Формулировка задачи: в зависимости от перечисленных критериев устанавливается максимальный вес продуктов 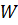 в случае поставленной задачи – это максимальная суточная калорийность. Необходимо составить сбалансированный рацион на день для школьника, который покажет, как часто в рацион нужно включать продукты питания той или иной категории, указанной в таблице 2, для получения максимального эффекта от потребляемых продуктов [4, 5].
в случае поставленной задачи – это максимальная суточная калорийность. Необходимо составить сбалансированный рацион на день для школьника, который покажет, как часто в рацион нужно включать продукты питания той или иной категории, указанной в таблице 2, для получения максимального эффекта от потребляемых продуктов [4, 5].
Каждая категория имеет свой вес 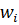 и прибыль (эффект)
и прибыль (эффект) 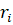 . Вес – это калорийность на 1 порцию потребляемого продукта.
. Вес – это калорийность на 1 порцию потребляемого продукта.
В нашей задаче значение (прибыль или эффект) для каждого продукта установлено в зависимости от следующих оценок: продукт является полезным для человека, несет насыщение, дает энергию, не вызывает аллергии. Показатель 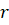 измеряется в баллах.
измеряется в баллах.
Таким образом, необходимо составить такой перечень категорий продуктов с указанным количеством, чтобы значение принесло максимальный эффект.
Поставленная задача относится к категории задач о загрузке рюкзака с ограничениями, т.к. мы обязаны включить каждую категорию продуктов в дневной рацион хотя бы один раз. Следовательно, исходя из данных таблицы 1, приходим к выводу, что решить данную задачу возможно только при помощи метода динамического моделирования.
Для этого разработаем математическую модель поставленной задачи.
Пусть 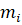 – количество предметов
– количество предметов 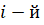 категории продуктов, подлежащей загрузке, тогда общая задача об оптимальной загрузке имеет вид следующей целочисленной задачи линейного программирования:
категории продуктов, подлежащей загрузке, тогда общая задача об оптимальной загрузке имеет вид следующей целочисленной задачи линейного программирования:
Максимизировать 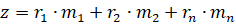 при условии, что
при условии, что
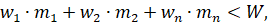
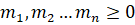 и целые.
и целые.
Следует учитывать, что 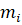 – количество предметов не должно превышать ни по одной из категорий значения
– количество предметов не должно превышать ни по одной из категорий значения 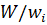 .
.
Максимальная прибыль же будет соответствовать сумме прибыли, полученной на предыдущем шаге и прибыли текущей, при условии, что вес предметов на предыдущем шаге не меньше, веса предмета текущего шага. Если же это условие не выполняется, то прибыль текущего шага не прибавляется.
В качестве инструмента решения поставленной задачи использовали математическое программирование в электронной таблице Microsoft Office Excel 2010.
Окно программы с исходными данными приведено на рисунке (рис. 1).
В ячейках B3, B4 пользователь выбирает соответствующие ему критерии – возраст и физическую активность. В зависимости от выбора пользователя программа сама выбирает максимальную суточную калорийность и заносит значение в ячейку B4. Данное действие реализовано при помощи функции ЕСЛИ() и логических функций И, ИЛИ.
Вариант ее использования приведен ниже:
=ЕСЛИ(И(B2="Дети от 9 до 13 лет";ИЛИ(B3=AH2;B3=AH3));2000;2500)
Далее в диапазоне B10:B17 вносятся значения wi, а в диапазон C10:C17 – ri.
В ячейку I18 вводим формулу для поиска максимума целевой функции z.
=СУММПРОИЗВ(C10:C17;I10:I17).
Для решения оптимизационной задачи в Excel 2010 используется инструмент Поиск решения, который находится на вкладке Данные. Окно заданных значений и ограничений приведено на рисунке (рис. 2).
Важно указать, что искомые значения mi должны быть целыми значениями в окошке «В соответствии с ограничениями». Диапазон изменяемых значений – это столбец I10:I17, т.е. искомые значения mi.Также важно ограничить максимальную калорийность, установить ее равной ячейке B4.
После нажатия на кнопку «Найти решение» программа подбирает искомые оптимальные значения и рассчитывает максимальную прибыль. Вариант решения с критериями подросток от 14 до 18 с легким физическим трудом представлен на рисунке (рис. 3).
Таким образом, делаем вывод, что рацион школьника четырнадцати лет с легкими физическими нагрузками должен содержать молочные продукты не менее двух раз, фрукты и овощи 4 раза и т.д. согласно данным в столбце mi, который мы видим на рисунке (рис. 3). При таком наборе школьник получит максимальный эффект от рациона питания.
Если же мы изменим критерий_2 на «умственный труд», то граничная калорийность станет 2000 ккал, а эффект снизится на 10 позиций и позиция «сладости» из рациона питания исключается программой.
Вариации поисковых решений могут меняться в зависимости от тех ограничений, которые будут установлены для целевой функции в окне программы «Поиск решений».
Результаты и обсуждение
Результаты исследований были представлены на школьном семинаре научного совета в марте 2024 г., а также на городском фестивале детских исследовательских проектных работ и реферативных работ среди обучающихся 6-8 классов «Юный исследователь» в апреле 2024 г. Оргкомитет конкурса оценил высокий уровень подготовки проведенных исследований, выдан диплом за занятое второе место в конкурсе.
Выводы
Поиски оптимальных решений привели к созданию специальных математических методов. В качестве инструмента решения оптимизационных задач используется математическое программирование (планирование).
Применение математических моделей позволяет использовать средства вычислительной техники для анализа допустимых решений, поиска наиболее рационального оптимального решения.
Математическое моделирование – мощный инструмент анализа данных, исследования определенных зависимостей. Оптимизация – один из методов математического моделирования, заключающийся в получении наилучших результатов при соответствующих условиях.
В ходе исследования задачи о рюкзаке были выявлены три основных методы решения. Они протестированы на практических задачах, выполнено аналитическое сравнение методов по скорости решения, по точности. Изучены методы полного перебора, динамического программирования. Так же был рассмотрен метод ветвей и границ, но как сокращение полного перебора.
Все методы разделены на две группы. Первая группа – точные методы, сюда входят алгоритмы динамического программирования, полный перебор и метод ветвей и границ. Вторая группа – приближенные методы, к таким методам относится жадный алгоритм. Выбор использования того или иного метода неординарный вопрос. В зависимости от постановки задачи, а так же от того, какие цели поставлены следует выбирать тот или иной метод.
Определено, что для поиска оптимального решения для задачи с исходными данными более 3 вариаций самым точным алгоритмом является динамическое программирование. Если же точность решения не так важна, или входные данные таковы, что ни один из точных методов не работоспособен, остается применять только приближенные алгоритмы.
В качестве инструмента реализации динамического программирования в работе рассмотрена программа Microsoft Office Excel. Электронная таблица предлагает широкий ассортимент функций для решения задач оптимизации, одним из них является инструмент «Поиск решений». На основании использования данного инструмента реализована задача поиска оптимального решения задачи об оптимальной загрузке относительно собственно разработанной математической модели, позволяющей формировать сбалансированный набор продуктов питания школьника на день. В будущем планируется модернизировать представленную математическую модель, в плане расширения функций, добавить возможность формировать рацион в зависимости от вкусовых предпочтений, а также с учетом хронических заболеваний. Разработанная в работе математическая модель доказывает тот факт, что задача о рюкзаке очень важна даже в решении задач реальной жизни, а не только в экономике и прикладной математике.
Реализация задач об оптимальной загрузке показывает, что проблема выбора оптимального решения часто возникает также враспределении ресурсов, когда существует необходимость принятия решения по выбору из набора неделимых проектов или задач с фиксированным бюджетом или временными ограничениями соответственно.
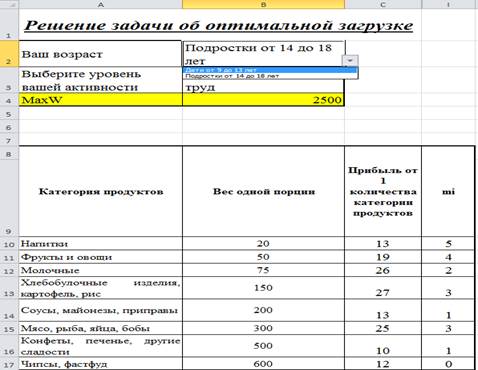
Рисунок 1 – Условия для решения задачи о загрузке рюкзака
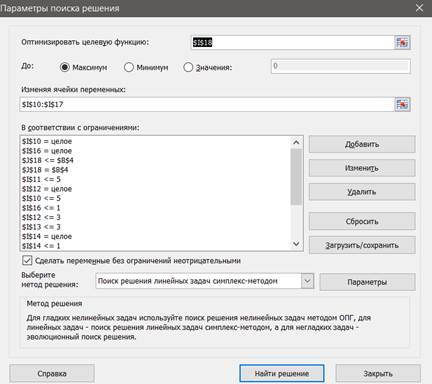
Рисунок 2 – Настройка параметров поиска решений
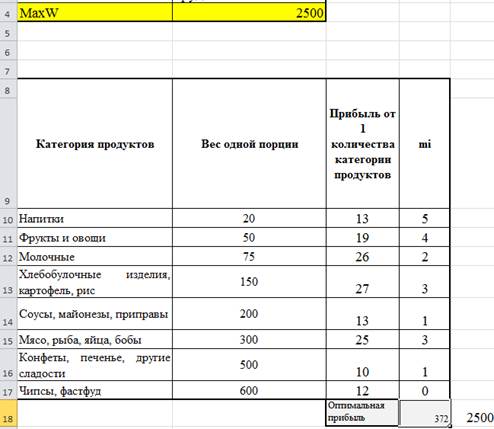
Рисунок 3 – Вариант максимума функции при введенных критериях MaxW=2500 ккал
Библиографическая ссылка
Гончаров К.С. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ // Старт в науке. 2024. № 4. ;URL: https://science-start.ru/ru/article/view?id=2413 (дата обращения: 13.03.2026).

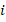
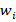
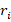 , баллы
, баллы