“Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их”.
Д. Пойя
Введение
Размышляя над какой-то задачей, мы начинаем увлекаться математикой. Многие ученики сталкиваются с задачами на нахождение площади треугольника, параллелограмма, многоугольника и других геометрических фигур по рисунку на клетчатой бумаге. Такие задачи чаще всего встречаются в ВПР по математике, а также они есть в контрольно-измерительных материалах ОГЭ и ЕГЭ. Применяя правила и теоремы из геометрии, ученик может запутаться или забыть, да и к тому же уходит много времени на дополнительное построение, а в условиях экзамена дорога каждая минута. Чтобы не тратить много усилий, времени и не вспоминать впопыхах теоремы, аксиомы, правила, существует теорема Пика, с помощью которой можно без проблем и траты времени вычислить площадь фигуры, расположенной на клетчатой бумаге. Но в чём же заключается особенность таких задач, какие методы и приёмы используются для решения задач на клетчатой бумаге?
Актуальность: Выбор темы проекта не случаен. Способы нахождения площади многоугольника, нарисованного на клетчатой бумаге, очень интересная и актуальная тема, особенно, при подготовке к экзаменам. При решении задач по математике и геометрии часто встречаются задачи, где нужно вычислить площадь фигур. Если фигура сложная, то её площадь находить довольно долго одним из способов: либо достроим до известной фигуры, либо разделим на фигуры.
Гипотеза: мы считаем, что вычисление площадей сложных фигур с помощью формулы Пика легче, чем вычисление методом достраивания и разбивания фигур на части и его может освоить каждый школьник.
Объект исследования: формула Пика для вычисления площадей многоугольников.
Предмет исследования: применение формулы Пика при решении задач, на нахождение площади фигур, изображённых на клетчатой бумаге.
Таким образом, целью моего исследования является: донести и объяснить материал о Формуле Пика учащимся 8-9 классам; доказать рациональность использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге. Изучение данной темы поможет лучше подготовиться к олимпиадам и экзаменам.
Задачи:
1. Изучить методы вычисления площадей сложных фигур на клетчатой бумаге.
2. Научиться применять формулу Пика для вычисления площадей различных фигур.
3. Сделать видео разбор для учащихся старших классов.
4. Сравнить и проанализировать результаты исследования проведенных среди старшеклассников.
5. Донести учащимся рекомендации по применению формулы Пика при решении задач ОГЭ и ЕГЭ.
Методы:
1. Системный анализ
2. Обобщение
3. Сравнение
4. Поиск
Теоретическая часть
Методы вычисления площадей
В процессе изучения математики, мы заметили, что площади одних и тех же фигур можно находить различными способами. В быту мы часто сталкиваемся с задачами нахождения площади. Например, высчитать площадь стен, на которые необходимо наклеить обои, или вычислить площадь напольного покрытия. Вычисление площади квадрата, прямоугольника и прямоугольного треугольника не вызвало у нас затруднений.
В жизни очень часто мы сталкиваемся с тем, что нам приходится находить площадь геометрической фигуры неправильной формы. Как это сделать?
Наверное, проще всего разбить его на прямоугольные треугольники и прямоугольники, площади которых нетрудно вычислить по формулам.
Способы нахождения площадей фигур на клетчатой бумаге.
- Площадь фигуры как сумма площадей ее частей
Найти площадь фигуры №1 на рисунке 1 (клетки размером 1х1 см). Разбиваем данную фигуру на четыре части, и находим площадь каждой части. Затем складываем все части, и получаем площадь данной фигуры.
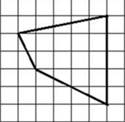
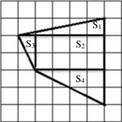
Рис 1. Фигура №1
Разобьем многоугольник на четыре геометрические фигуры:
S=S1+ S2+ S3+S4
Площадь прямоугольного треугольника находится S1= ½ · 5 · 1 = 2,5 см2;
Площадь прямоугольника находится S2=4·2=8 см2
Площадь прямоугольного треугольника находится S3= ½ · 1· 2= 1 см2
Площадь прямоугольного треугольника находится S4= ½ · 2 · 4= 4 см2
S= 2,5+8+1+4= 15,5 см2.
Ответ: 15,5 см2.
- Площадь фигуры как часть площади прямоугольника
Найти площадь фигуры на рисунке 2 фигура №2 (клетки размером 1х1см). Опишем около данной фигуры прямоугольник. Из площади прямоугольника (в данном случае квадрата) вычтем площади полученных фигур:
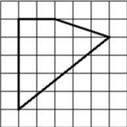
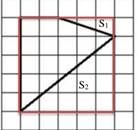
Рис. 2. Фигура №2
S= Sпр. – S1 – S2
Sпр.=5.5=25 см2;
S1= ½ .3.1=1,5 см2;
S2= ½ .4.5=10 см2;
S= 25-1,5-10=13,5 см2.
Ответ: 13,5 см2 .
Вывод: анализ показал, что вычислять площади фигур «достраиванием» или «разбиением» долгий процесс и требует большого количество промежуточных действий. Оказывается, есть другой способ для вычисления площади фигур на клетчатой бумаге, используя Формулу Пика.
Формула Пика
Формула Пика(илитеорема Пика) - классический результат комбинаторной геометрии и геометрии чисел, согласно которому площадь многоугольника с целочисленными вершинами равна:
|
S = В + Г : 2 - 1 |
ГдеВ- количество целочисленных точек внутри многоугольника, а Г- количество целочисленных точек на границе многоугольника.
Доказательство:
Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами в декартовой системе координат.
Теорема Пика. Нахождение площади решётчатого многоугольника (Рис.3 Многоугольник)
S = В + Г / 2 - 1, где В — к-во целых точек внутри многоугольника, Г — к-во целых точек на границе многоугольника. В = 7, Г = 8, S = В + Г/2 - 1 = 10
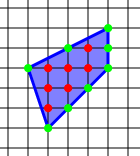
Рис. 3. Многоугольник
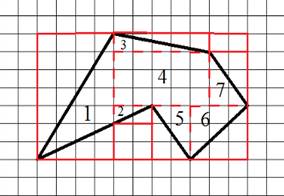
Пример 1.
I способ. Достроим до прямоугольника. (Рис.4 Многоугольник)
|
Рис. 4. Многоугольник |
Решение: 1) S1 = 4 . 7 – ((4 . 7 : 2) + (2 . 4 : 2)) = 28 – 18 = 10 см.2 2) S2 = 2 . 1 : 2 = 1 см.2 3) S3 = 5 . 1 : 2 = 2,5 см.2 4) S4 = 5 . 3 = 15 см.2 5) S5 = 2 . 3 : 2 = 3 см.2 6) S6 = 3 . 3 : 2 = 4,5 см.2 7) S7 = 2 . 3 : 2 = 3 см.2 8) SФ = S1 + S2 + S3 + S4 + S5 + S6 + S7 9) 10 + 1 + 2,5 + 15 + 3 + 4,5 + 3 = 39 см.2 Ответ: 39 см.2 |
|
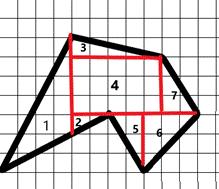
II способ. Формула Пика. (Рис.5 Многоугольник)
Рис. 5. Многоугольник
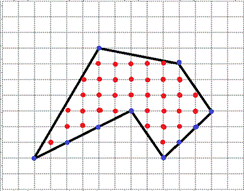
Пример 2. I способ. Разобьем на геометрические фигуры. (Рис. 6 Многоугольник)
(Рис.6 Многоугольник)
|
Решение:
Г=10 (синие) В=35 (красные) S = 35 + 10:2-1 = 39
Решение: 1) S1 = (4 . 5) : 2 = 10 см.2 2) S2 = (1 . 2) : 2 = 1 см.2 3) S3 = ( 1 . 5) : 2 = 2,5 см.2 4) S4 = 3 . 5 = 15 см.2 5) S5 = ( 2 . 3 ) : 2 = 3 см.2 6) S6 = ( 3 . 3) : 2 = 4,5 см.2 7) S7 = ( 2 . 3 ) : 2 = 3 см.2 8) Sф = 10 + 1+ 2,5 + 15 + 3 + 4,5 + 3 = 39 см.2 Ответ : Sф = 39 см.2
|
Доказательство производится в несколько этапов: от самых простых фигур до произвольных многоугольников:
Единичный квадрат. В самом деле, для него S = 1, В = 0, Г = 4, формула верна.
Прямоугольник со сторонами, параллельными осям координат. Пусть a и b длины сторон прямоугольника. Тогда: S = ab, В = (a-1) (b-1), Г = 2(a+b). Подстановка показывает, что формула Пика верна.
Прямоугольный треугольник с катетами, которые параллельны осям координат. Любой такой треугольник можно получить отсечением некоторого прямоугольника его диагональю. Обозначив через с число целых точек, лежащих на диагонали, можно показать, что формула Пика выполняется для такого треугольника, независимо от значения S.???
Любой треугольник. Такой треугольник может быть превращён в прямоугольник приклеиванием к его сторонам прямоугольных треугольников с катетами, параллельными осям координат (надо не более 3 таких треугольников). Отсюда получаем корректность формулы Пика для любого треугольника.
Произвольный многоугольник. Для доказательства разобьём его на треугольники с вершинами в целых точках. Для одного треугольника формула Пика доказана. Можно доказать, что при добавлении к многоугольнику треугольника формула Пика сохраняет свою корректность. Отсюда по индукции следует, что она верна для любого многоугольника.
Заключение
Любители головоломок увлекаются решением задач на клетчатой бумаге, прежде всего потому, что универсального метода решения таких задач не существует, и каждый, кто берётся за их решение, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению, поскольку здесь не требуется глубокого знания геометрии. Вместе с тем, задачи на клетчатой плоскости не являются несерьёзными или бесполезными, они не так уж и далеки от серьёзных математических задач.
Формула Пика проста в понимании и удобна в применении. Во-первых, достаточно уметь считать, делить на 2, складывать и вычитать. Во-вторых, можно найти площадь и сложной фигуры, не затратив много времени. В-третьих, эта формула работает для любого многоугольника.
Недостаток в том, что Формула Пика применима только для фигур, которые нарисованы на клетчатой бумаге и вершины лежат на узлах клеток.
При выполнении нашей работы мы рассмотрели решение задач на вычисление площади многоугольников неправильной формы разными способами. Ознакомление учащихся с формулой Пика особенно актуально накануне сдачи ЕГЭ и ГИА. С помощью этой формулы можно без проблем решать большой класс задач, предлагаемых на экзаменах, — это задачи на нахождение площади многоугольника, изображённого на клетчатой бумаге.
Маленькая формула Пика заменит учащимся целый комплект формул, необходимых для решения таких задач. Формула Пика будет работать «одна за всех…»!
Формула Пика — это настоящее спасение для тех учеников, которые так и не смогли выучить все формулы для вычисления площадей фигур, для тех, кто так и не уяснил до конца, как выполнить разбиение фигуры или дополнительное построение, чтобы подобраться к вычислению её площади «через знакомых».
С другой стороны, для тех, кто площадь многоугольника, изображённого на клетчатой бумаге, умеет находить с помощью вышеперечисленных приёмов, формула Пика послужит дополнительным инструментом, с помощью которого можно будет решить задачу ещё и этим способом (и тем самым проверить правильность своего предыдущего решения, сверив полученные ответы). Материал для самообразования в приложении.
Проанализировав способы решения задач на вычисление площадей, можно сделать следующие выводы:
1. Формула Пика даёт быстрое и простое решение задач на нахождение площади фигуры на клетчатой бумаге, вершины которой лежат в узлах решётки, то есть нахождения площадей многоугольников.
2. Основное условие для применения формулы Пика: у многоугольника, изображённого на клетчатой бумаге (решётке), должны быть только целочисленные вершины, то есть они обязательно должны находиться в узлах решётки.
3. Использование формулы Пика для нахождения площади кругового сектора или кольца нецелесообразно, так как она даёт приближённый результат.
4. Формула Пика не применяется для решения задач в пространстве.
При помощи формулы Пика легко вычислить площадь многоугольника на плоскости даже самой причудливой формы.
Библиографическая ссылка
Рассохина Е.О. ТЕОРЕМА ПИКА // Старт в науке. 2022. № 6. ;URL: https://science-start.ru/ru/article/view?id=2237 (дата обращения: 05.02.2026).