Введение
Теория игр-метод изучения оптимальных решений для различных задач. Мы рассмотрим данную теорию с экономической стороны. Она помогает лучше понять и описать взаимодействие между различными компаниями, другими участниками рынка. К примеру, существуют различные экономические модели по всевозможным ситуациям. В моем проекте я создам пособие по решению различных экономических конфликтов со стороны разных игроков.
Все люди являются непосредственными участниками рынка, большинство из них являются покупателями. Они заинтересованы в приобретении товара или услуги по определенным критериям. Но по каким именно? По ним и строится стратегия покупателя.
Рассмотрим ситуацию. Первый игрок – покупатели. Каждый из них выбирает для себя товар, из представленного множества вариантов он выбирает подходящий себе, смотря на разные критерии, такие как: качество, годность, популярность и т. д. Он выбирает для себя определенную модель поведения, которая ему наиболее выгодна.
В свою очередь, второму игроку - изготовителю нужно составить свою оптимальную стратегию по продаже данной продукции, чтобы заинтересовать в этом наибольшее число покупателей. Стратегия составляется путем отбора различных факторов, влияющих на продажи товара.
Исходом данной игры будет либо выигрыш второго игрока – продажа товара большинству покупателей, либо проигрыш – незаинтересованность людей, либо ничья – товар был продан, и деньги покрыли все расходы.
Сейчас была описана обычная схема купли-продажи с точки зрения теории игр. Как мы видим, эта теория применяется и используется как нами – обычными потребителями, так и производствами.
Основная часть
Основные термины.
Конфликт – ситуация, в которой затронуты интересы нескольких участников, называемых игроками.
Исход игры – это выигрыш, проигрыш или ничья, а также полученное вознаграждение.
Стратегия — умозаключения, из которых исходит выбор действий в игре. Стратегии бывают чистыми и смешанными.
Чистая стратегия – это стратегия, ориентированная на определенное поведение игрока-противника.
Смешанная стратегия – это стратегия, ориентированная на несколько возможных стратегий поведения игрока-противника. Числовые характеристики, выражающие интересы игроков – это значения платежной функции (функции выигрыша или проигрыша), которая задается матрицей (таблично) или аналитически.
Равновесие Нэша — это такой профиль стратегий, что ни один отдельно взятый игрок не захочет изменить свою стратегию, если стратегии оставшихся игроков останутся неизменными. Равновесие Нэша является основной концепцией решения теоретико-игровых задач. [Захаров, А. В., Теория игр в общественных науках. 2020, с. 21]
Модель поведения — присущая игроку стратегия либо стратегии.
Игра - математическая модель конфликта. Она характеризуется по:
· количеству игроков на парные и непарные;
· количеству стратегий на конечные и бесконечные;
· количеству информации на полные и исчерпывающие;
· выигрышу игроков на игру с нулевой и ненулевой суммой;
· взаимодействию игроков – коалиционные или бескоалиционные.
Задачи по Теории игр
Задача 1.
Существуют две компании по продаже процессоров: компания A и компания B. Первая компания предлагает определенную линейку процессоров A1, A2, A3, A4, а компания Б: B1, B2, B3, B4. Какую продукцию выгоднее производить каждой компании, учитывая затраты на их производство и выручку от проданной первой партии? Выбрать наиболее оптимальную стратегию компаниям, чтобы получить максимальную прибыль.
Решение:
компания А по производству процессоров выделяет 25 млн. дол. на закупку товара на реализацию. Имеется выбор между продажей процессоров Т1 или Т2. Ожидаемая прибыль зависит от того, какой товар Т1 или Т2 будет закупать конкурент В. Если оба будут закупать Т1, то ввиду конкуренции А понесет убытки в 7 млн. дол. Если оба будут закупать Т2, то по той же причине А понесет убытки в 3 млн. дол. Если А закупит Т1, а В закупит Т2, то прибыль А составит 21 млн. дол. Если А закупит Т2, а В закупит Т1, то прибыль А составит 17 млн. дол. Как лучше поступить игрокам при оптимальном поведении?
Обозначим стратегии игроков:
А1 – компания А закупает товар Т1,
А2 – компания А закупает товар Т2,
В1 – компания В закупает товар Т1,
В2 – компания В закупает товар Т2.
Платежная матрица имеет вид:
|
Ai |
B1 |
B2 |
|
A1 |
-7 |
21 |
|
A2 |
17 |
-3 |
p1 = 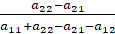 p2 =
p2 = 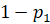 ,
,
q1= 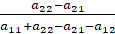 q2 =
q2 = 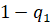 ,
,
v = 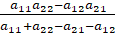 =7,
=7,
p1 = 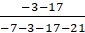 =
= 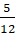 p2 =
p2 = 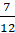 ,
,
q1= 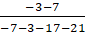 =
= 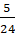 q2 =
q2 = 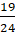 ,
,
v = 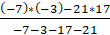 =7,
=7,
где pi и qj - вероятности чистых или доли чистых стратегий Ai и Bj в игре,
v – цена игры.
Следовательно, первому игроку выгодно реализовать обе стратегии А1 и А2 в долях 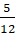 = 0,42 и
= 0,42 и 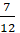 = 0,58, то есть произвести процессоры Т1, и Т2. При этом Т1 должен быть закуплен на сумму 10,5 млн. дол., а Т2 на сумму 14,5 млн. дол. Прибыль, независима от поведения соперника, составит 7 млн. дол. То же можно сказать и для игрока В (если, конечно, игра антагонистическая и выигрыш А — это проигрыш В). Нужно производить процессоры T1 на сумму 7/12 от запланированной – 14,5 млн. дол, а T2 на сумму 19/24 – 19,5 млн. дол.
= 0,58, то есть произвести процессоры Т1, и Т2. При этом Т1 должен быть закуплен на сумму 10,5 млн. дол., а Т2 на сумму 14,5 млн. дол. Прибыль, независима от поведения соперника, составит 7 млн. дол. То же можно сказать и для игрока В (если, конечно, игра антагонистическая и выигрыш А — это проигрыш В). Нужно производить процессоры T1 на сумму 7/12 от запланированной – 14,5 млн. дол, а T2 на сумму 19/24 – 19,5 млн. дол.
Задача 2.
Крупная сеть магазинов собирается закупить одну из линеек процессоров компании A. Всего можно выделить несколько линеек, доступных для закупки: A1, A2, A3, A4, A5. Успехом можно считать наиболее выгодную продажу данных товаров. Аналитики данной сети предложили 6 различных вариантов развития ситуации на рынке S1,S2, S3, S4, S5, S6. Прибыль сети для каждой альтернативы при каждой ситуации представлена матрицей выигрышей aij (млн. р./год):
|
Ai |
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
|
A1 |
7 |
2 |
9 |
11 |
8 |
6 |
|
A2 |
13 |
4 |
10 |
3 |
7 |
4 |
|
A3 |
10 |
7 |
6 |
11 |
9 |
5 |
|
A4 |
4 |
6 |
12 |
8 |
5 |
7 |
Решим данную задачу, рассмотрев ее при помощи различных критериев:
1) Критерий Лапласа.
Он основан на том, что все варианты развития данной игры «с природой» равновероятны. Для решения нам понадобится воспользоваться функцией полезности Fi для каждой альтернативы:
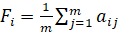 ,
,
где m – количество столбцов; 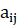 – стратегия, находящаяся в i-й cтроке и j–м столбце.
– стратегия, находящаяся в i-й cтроке и j–м столбце.
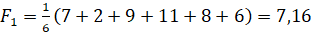 ,
,
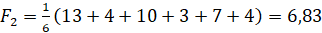 ,
,
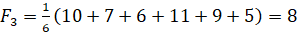 ,
,
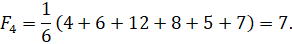
Функция полезности максимальна для варианта A4, следовательно, его и рациональней принять.
2) Критерий Вальда.
Он основывается на том, что произойдет самый плохой вариант и все риски, связанные с ним, нужно свести к минимальным. Для этого нужно выбрать худший (самое маленькое число в каждой строке матрицы) показатель привлекательности ai и выбрать альтернативу, для которой этот показатель максимален. В нашем случае:
a1=2; a2=3; a3=5; a4=4.
Здесь выгодно взять альтернативу A3, так как для нее показатель a3=5 максимален.
3) Критерий максимального оптимизма.
Этот критерий схож с критерием Вальда, только нужно искать строчку, где самый максимальный показатель. Это альтернатива A2 с показателем 13.
4) Критерий Сэвиджа.
В нем составляется матрица рисков rij, которая получается путем вычитания из максимального элемента столбца всех остальных элементов:
|
Ai |
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
|
A1 |
4 |
9 |
2 |
0 |
3 |
5 |
|
A2 |
0 |
9 |
3 |
10 |
6 |
9 |
|
A3 |
1 |
4 |
5 |
0 |
2 |
6 |
|
A4 |
8 |
6 |
0 |
4 |
7 |
5 |
Теперь нужно определить величину Bi для каждой альтернативы, которая будет равна максимальному риску (наибольшему числу в каждой строке): B1= 9; B2= 10; B3= 6; B4 = 8. Выбираем ту, для которой максимальный риск минимален. B3 минимально, принимаем альтернативу A3.
Задача 3.
Равновесием Нэша в рассматриваемой игре будет та ситуация, от которой ни одному из игроков не выгодно в одностороннем порядке отклоняться. В терминах отображений наилучшего ответа это определение запишется так: равновесие – это тот профиль стратегий, в котором стратегия каждого игрока входит во множество его наилучшего ответа на равновесную стратегию соперника.
Игрок A- покупатель, игрок B – консультант продуктового магазина. Покупатель имеет плохую репутацию в данном магазине, потому что он несколько раз попадался на краже товара. У него есть как минимум 2 стратегии поведения в магазине:
1) украсть товар;
2) повести себя честно и оплатить продукт, который он мог украсть.
Назовем эти стратегии «воровство» и «честность» соответственно.
У консультанта есть 3 стратегии:
1) проследить за покупателем и помешать ему в краже;
2) поверить игроку A и не следить за ним;
3) вызвать охранку для наказания нарушителя.
Назовем эти стратегии «слежка», «доверие» и «охрана» соответственно.
Определим выигрыши продавца и покупателя в каждой ситуации:
1. Покупатель украл товар, а консультант проследил за ним. Выигрыш покупателя равен 0, так как при его поимке он просто заплатит за товар утроенную стоимость и не получит никакого наказания, а у консультанта 1, так как он сохранит товар.
2. Покупатель украл товар, а продавец поверил ему. Выигрыш игрока A -1, а игрока B - -1, так как украденный товар будет вычтен из его зарплаты.
3. Покупатель украл товар, а консультант решил вызвать охрану, выигрыш покупателя -1, так как на него заведут административную ответственность, а выигрыш консультанта 1.
4. Покупатель повел себя честно, а продавец проследил за ним. Выигрыш покупателя 0, так как он ничего не украл, а продавца -1/2, так как он потерял свое время, но не потерял товар.
5. Покупатель повел себя честно, а продавец поверил ему. У обоих выигрыш 0, так как произошла обычная бытовая ситуация с покупкой и продажей товара.
6. Покупатель повел себя честно, а продавец вызвал охрану, покупателю выигрыш -1/2, так как он потерял время, а продавцу -1, так как он потерял время и свое, и охраны, а также на него могут завести административное дело в ответ, за обыск невиновного.
Построим матрицу:
A=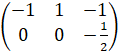 ,
,
B=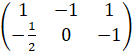 .
.
Наилучшие стратегии игроков:
A=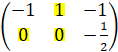 ,
,
B=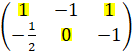 .
.
В данной задаче наиболее выгодной по равновесию Нэша будет только 1 стратегия, следовательно, можно выбрать стратегии «честность» и «доверие» соответственно игроку A и B.
Заключение
Итак, мы рассмотрели решение нескольких задач с помощью данной теории, применив к одной из них различные способы решения. На данных простых экономических задачах мы увидели, как именно используется Теория игр. Изучив мой материал, можно продолжить освоение данной теории и начать применять ее в более сложных задачах, которые могут быть основаны на примере различных ситуаций.
Библиографическая ссылка
Ример А.А. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕОРИИ ИГР // Старт в науке. 2022. № 2. ;URL: https://science-start.ru/ru/article/view?id=2184 (дата обращения: 05.02.2026).

 Bj
Bj