Введение
Актуальность исследования заключается в том, что в работе рассматриваются такие свойства биссектрисы треугольника, о которых в школьных учебниках даже не упоминается, но они вызывают интерес и значительно упрощают решение некоторых задач.
Цель работы: установление свойств биссектрисы угла треугольника, которые не изучаются в школе, но применяются при решении задач по геометрии и облегчают их решение.
Задачи исследования:
1) проанализировать информацию о свойствах биссектрисы треугольника из различных источников информации;
2) обобщить свойства биссектрисы угла и биссектрисы угла треугольника, которые изучаются в школьном курсе геометрии;
3) привести примеры их применения при решении задач по математике;
4) доказать малоизвестное свойство биссектрисы угла треугольника – лемму о дважды биссектрисе;
5) исследовать лемму о дважды биссектрисе для остроугольных, прямоугольных и тупоугольных треугольников;
6) найти и решить задачи на применение леммы о дважды биссектрисе треугольника;
7) установить наличие других малоизвестных свойств биссектрисы треугольника.
Предмет исследования: малоизвестные свойства биссектрисы треугольника.
Гипотеза: в ходе выполнения работы будут найдены свойства биссектрисы угла треугольника, которые помогут при решении задач.
В учебной литературе вопрос о свойствах биссектрисы угла треугольника освещён в недостаточной мере для решения задач. Для раскрытия темы работы было проведено моделирование леммы о дважды биссектрисе и задач, проведён эксперимент «Исследование леммы о дважды биссектрисе в остроугольном, прямоугольном и тупоугольном треугольниках».
Методы исследования: анализ учебников, справочной математической литературы, построения с помощью циркуля и линейки, компьютерное моделирование математических объектов с помощью ИГС GeoGebra, анализ, сравнение, сопоставление и обобщение объектов, полученных в результате моделирования, обобщение найденных с помощью компьютерного моделирования закономерностей, проверка выдвинутых гипотез, аналитические рассуждения.
Основная часть
В геометрии существует огромное количество интересных фактов о различных элементах. Одним из этих элементов в треугольнике является биссектриса. На протяжении многих веков математики находили свойства, связанные с ней, однако некоторым из них не уделяется внимание вучебниках[1].
Знакомство с тетрадью с печатной основой «Бенефис биссектрисы внутреннего угла треугольника», созданной учениками нашей школы на занятиях элективного курса по геометрии в 2014 году, вызвало интерес у автора работы, поскольку одно свойство доказывалось 11 разными способами [2]. Это можно назвать первым неожиданным сюрпризом биссектрисы угла треугольника.
Особое внимание автор обратил внимание на задачу, в которой говорится об интересном свойстве биссектрисы угла треугольника:
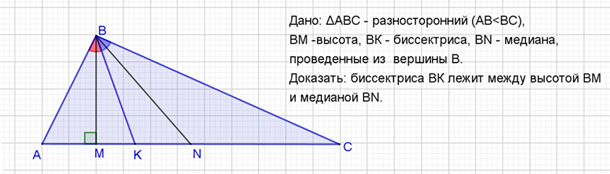
Доказательство: AK+KC=AC. KC>
AC. По свойству биссектрисы угла треугольника 
= 
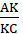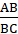. AB<BC, тогда AK<KC. Значит, AK<AC. ТочкаК лежит между точками А и N. В ?АВK точка М лежит между точками А и К. Тогда точка K лежит между точками М и N.
Значит, биссектриса лежит между высотой и медианой, проведенных из той же вершины треугольника. Это стало для автора вторым сюрпризом биссектрисы треугольника.
После доказательства было проведено моделирование в ИГС Geogebra для различных видов треугольника и было установлено, что данное свойство справедливо для любого разностороннего треугольника.
Лемма о дважды биссектрисе
Следующее свойство было получено во время решения задачи, предложенной научным руководителем.
Задача. В остроугольном ?АВС из вершины С проведены высота, биссектриса и отрезок, проходящий через центр описанной окружности до пересечения с противоположной стороной. Углы А и В равны соответственно 68?и 34?. Сравнить углы HCL, LCM и HCM.
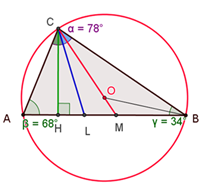
Решение. ΔACB–∠C=180?–(∠A+∠B)=78?;
ΔACH, ∠H=90?, ∠A=68?; ∠ACH=∠H–∠A=22?;
ΔACL, CL–биссектриса ∠ACB, ∠ACL=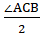
=39?.
∠HCL=∠ACL–∠ACH=39?–22?=17?.
∠COB–центральный угол, ∠CAB–вписанный угол, которые опираются на одну и ту же дугу. ∠COB=2∠CAB=68?×2=136?, ΔCOB–равнобедренный, ∠OCB=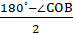
=22?.
∠LCM=∠LCB–∠MCB=39?–22?=17?.
∠HCL=∠LCM=17?
Значит, CL–биссектриса угла ∠HCM, стороны которого являются высотой и отрезком, проходящим через центр описанной окружности, проведенные из той же вершины данного треугольника.
В ИГС Geogebra было выполнено моделирование различных условий данной задачи в остроугольном, прямоугольном и тупоугольном треугольниках и проведено исследование, в результате которого было установлено, что ∠OAL=∠LAH в любом виде треугольника и при любых углах A и B.
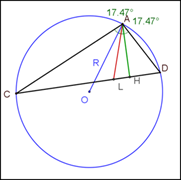
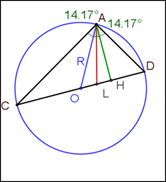
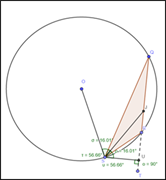
Позже оказалось, что у данного свойства есть своё название в научной литературе – лемма о дважды биссектрисе [3].
Лемма формируется следующим образом: биссектриса AL треугольника АВС является также биссектрисой угла ОАН, где O–центр окружности, описанной около треугольника АВС, АН–его высота.
Это уже третий сюрприз биссектрисы угла треугольника.
Это свойство довольно часто можно использовать при решении задач [3]. В работе приведены примеры использования леммы о дважды биссектрисе для решения задач на вычисление, доказательство и построение.
Задача на вычисление.
Дано: в треугольнике АВС высота hа и медиана mа делят угол А на три равные части.
Найти угол А.
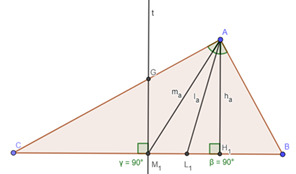
Решение. Проведем биссектрису AL1= lа и медиану АМ1= mа. Поскольку углы CAM1 и H1AB равны, то равны углы M1AL1 и L1AH1. Следовательно, центр O окружности, описанной около треугольника АВС, лежит на медиане mа. Но и серединный перпендикуляр t к стороне ВС содержит точку О. Значит, точки O и M1 совпадают. Тогда ВС–диаметр и ∠ВАС=90?.
Ответ: ∠A=90?.
Задача на доказательство.
Дан треугольник АВС. Серединный перпендикуляр к стороне ВС и продолжение биссектрисы la пересекаются в точке Q.
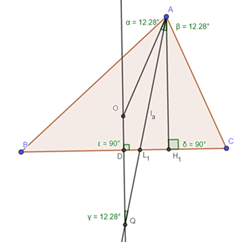
Доказать, что точка Q лежит на окружности с центром O, описанной около треугольника АВС.
Доказательство. Проведем высоту АН1 и радиус ОА. ∠OAL1=∠L1AH1 (следует из леммы). Но ∠ L1AH1=∠OQA – как внутренние накрест лежащие при параллельных прямых (АН1 ?? ОQ). Следовательно, треугольник AOQ–равнобедренный, причем OQ=ОА=Rокр. Значит, точка Q принадлежит окружности, описанной около треугольника АВС.
Задачи на построение.
Построить треугольник АВС по высоте ha, медиане maи биссектрисе la, проведенным из вершины А.
Решение.Треугольники АН1L1 и АН1М1 можно легко построить по катету и гипотенузе. Из вершины А проведем луч n под углом, равным углу Н1AL1. Согласно лемме, луч n содержит центр O окружности, описанной около треугольника АВС. Перпендикуляр t к прямой М1Н1, проходящий через точку М1, также содержит точку O. Таким образом, O–точка пересечения nи t.
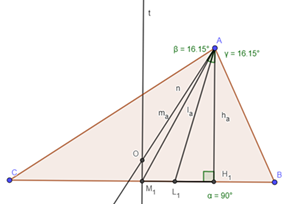
Стоит отметить, что экспериментальным путем было установлено, что данная задача имеет решение только, если медиана длиннее биссектрисы, а биссектриса длиннее высоты.
Ещё одно полезное свойство
Было установлено и доказано ещё одно свойство биссектрисы треугольника. Его можно применить не так часто, как лемму о дважды биссектрисе, но некоторые задачи оно упрощает.
Свойство: в прямоугольном треугольнике угол между медианой и биссектрисой прямого угла равен полуразности острых углов прямоугольного треугольника.
Дано: ΔABC; ∠B=90?; AE=EC; ∠ABD=∠CBD.
Доказать: ∠DBE=0,5|∠C–∠A|.
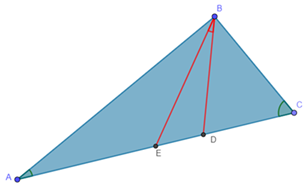
Доказательство: так как ΔABC–прямоугольный, то E–центр описанной окружности. Значит, AE=EB=Rокр, ∠A=∠EBA, но и AE=EC, следовательно, ΔEBC–равнобедренный, ∠C=∠EBC. ∠A+∠DBE=∠C–∠DBE. Тогда 2∠DBE=∠C–∠A. Значит, ∠DBE=0,5|∠C–∠A|.
Это уже четвертый сюрприз биссектрисы угла треугольника.
Автором была решена задача на вычисления, использующая данное свойство:
Дано: в прямоугольном треугольнике угол между биссектрисой и медианой, проведенными из вершины прямого угла, равен 13?.
Найти: ∠A, ∠B.
Решение:
∠KCM=0,5|∠A–∠B|. Тогда ∠A=∠B+2∠KCM.
∠A+∠C+∠B=180?; ∠B+2∠KCM+90?+∠B=180?.
2∠B=180?–90?–26?=64?; ∠B=32?. ∠A=180?–90?–32?=58?.
Ответ: ∠A=58?; ∠B=32?.
Заключение
В результате выполнения работы:
1)была подтверждена гипотеза (в ходе выполнения работы будут найдены свойства биссектрисы угла треугольника, которые помогут при решении задач), достигнута цель (установление свойств биссектрисы угла треугольника, которые не изучаются в школе, но применяются при решении задач по геометрии и облегчают их решение), выполнены задачи;
2)было показано, что применение «Леммы о дважды биссектрисе треугольника» упрощает решение задач на вычисление, доказательство и построение.
Библиографическая ссылка
Долгобородов С.В. СЮРПРИЗЫ БИССЕКТРИСЫ ТРЕУГОЛЬНИКА // Старт в науке. – 2021. – № 5. ;URL: https://science-start.ru/ru/article/view?id=2106 (дата обращения: 26.04.2024).