Тезисы
Задачу «Колодец Лотоса» или «Задачу Фараона» можно отнести к разряду изящных головоломок, подкупающих простотой своей формулировки. С позиций сегодняшнего дня уже не столь важно, была она выдумана писателем-фантастом Казанцевым или просто обозначена три тысячелетия назад древнеегипетскими жрецами, все равно над ней «ломают головы» по сей день не только математики, но и программисты.
I.Введение
Помни: замурованный, ты выбей на камне цифры,
подай его через отверстие для света и воздуха.
Здесь ответ: что это за цифры?
Это слова, взятые из книги писателя-фантаста А.П.Казанцева «Колодец Лотоса», которую я прочитала этим летом. Её сюжет меня заинтересовал. Завязка рассказа такова. Археолог Детрие, проводящий раскопки храма бога Ра в древнеегипетском городе Гелиополисе, обнаруживает надпись, в которой излагается условие следующей задачи:
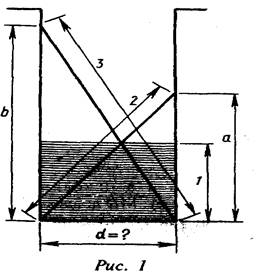
В колодец (см. рис. 1) погружены две тростинки длиной 2 и 3 меры. Вода доходит до точки их пересечения, которая находится выше дна колодца ровно на одну меру. Требуется определить диаметр колодца.[ Казанцев, 1975]
Тот, кто сможет решить эту задачу, становится жрецом бога Ра. Но если соискатель этого высокого звания потерпит неудачу, то погибнет, замурованный в камере возле колодца Лотоса. Чтобы разобраться в сути задачи, археолог вызывает из Парижа своего друга - профессионального математика, графа де Лейе. Тому удается с помощью достаточно сложных методов аналитической геометрии и алгебры составить уравнение четвертой степени с одним неизвестным. После этого по методу итальянского ученого XVI в. Феррари можно получить точное решение. Вывод уравнения в рассказе неоправданно сложен.[Казанцев, 1975]
Писатель-фантаст, закрутивший сюжет, на основе выдуманных им трогательных взаимоотношениях царицы и зодчего, мог придумать и задачу, ставшую испытанием для будущего жреца-зодчего. До начала своей писательской карьеры А.П. Казанцев был инженером и поэтому знал математику. Его рассказ интересен тем, что кроме формулировки задачи предложен один из вариантов решения задачи, доступный кандидатам на звание жреца. Этот метод состоит в непосредственном измерении диаметра колодца Лотоса с помощью тростинок. После довольно замысловатых манипуляций, использующих мокрые части тростинок, Сененмоту удается получить приближенное значение диаметра колодца d, равное 37/30. [Белянин,2017]
Гипотеза: можно ли утверждать, что задача о колодце Лотоса соединяет алгебру и геометрию, демонстрируя неразрывную связь этих двух дисциплин.
Объект исследования: задача Фараона или задача «Колодец Лотоса».
Предмет исследования: различные методы решения задачи о колодце Лотоса.
Цель исследования: показать многообразие подходов при решении одной геометрической задачи из занимательной математики.
Задачи исследования:
? изучить литературу по данной теме;
? выяснить: задача «Колодец Лотоса» - миф или реальность;
? решить занимательную геометрическую задачу «Колодец Лотоса» разными способами;
? обосновать геометрическую неразрешимость задачи Фараона;
? решить уравнение, составленное графом де Лейе в фантастическом рассказе А.П.Казанцева «Колодец Лотоса»;
? провести анкетирование для выяснения значимости изучения данной задачи;
? создать буклет «Колодец Лотоса» - загадка из Древнего Египта»
Методы исследования: эмпирические, а именно, изучение разнообразных источников информации, взятые из статей журнала «Математика в школе», анализ полученных сведений и опрос в виде анкетирования, чтобы глубже заглянуть в изучаемую проблему, составить диаграммы; теоретические: анализ и синтез, чтобы лучше понять материал и получить общее представление об изучаемом явлении (задаче Лотоса). Аналогия, где мы решали уравнения четвертой степени по принципу Феррари.
Выводы
На стене древнеегипетского храма под текстом данной задачи было обнаружено пояснение, из которого следует, что эта задача служила испытанием для желающих стать жрецами бога Ра. Вошедший в комнату для решения этой задачи оказывался, отрезан от внешнего мира, так что решивший ее становился жрецом, а не решивший умирал голодной смертью. Предупреждение под текстом задачи заканчивалось словами:
"Через стену колодца Лотоса прошли многие, но мало кто стал жрецом бога Ра. Думай. Цени свою жизнь. Так советуют тебе жрецы бога Ра". [Казанцев, 1975]
Заметим, что способ, которым могли бы воспользоваться египетские жрецы при отборе достойных кандидатов в жрецы, нам не известен. Можно только предполагать, что он был все же геометрическим, так как сколько-нибудь развитой техники решения уравнений тогда еще не было. Может быть, у кого-то это получится?
В работе описаны не все методы решения этой интересной задачи, а лишь те, в которых мы разобрались и которые будут понятны для восприятия.
Это аналитический способ, где составляется уравнение 4-й степени. Мы, в первой четверти изучали «Многочлены», но с методом Феррари пришлось ознакомиться самостоятельно, так как уравнение оказалось нестандартным и легко не решается. Инженерный подход к задаче заключался в том, что он опирался не на теоретическое решение, а на получение практического результата, т.е. мы немножко коснулись эстетики Древнего Египта. Так как при написании нашей работы мы опирались в основном на статьи, то в своей работе без внимания оставили программный подход к решению задачи, который был затронут в статье Р.М. Нижегородцева. [Нижегородцев, 1997]. Поэтому исследование можно продолжить в дальнейшем.
Также, мы подтвердили гипотезу, что задача о колодце Лотоса соединяет алгебру и геометрию. Без знаний геометрии нельзя составить уравнение или систему уравнений, а без алгебры - решить их. В работе цель достигнута, задачи выполнены. Задача Фараона или «Колодец Лотоса» уникальна. Не одно столетие эта загадка волнует умы человечества. До сих пор мы не можем быть уверенными в достоверности ее решения. Это и делает ее интересной для настоящих и будущих исследователей.
Библиографическая ссылка
Белозоров И.А., Третьякова Е.И. ЕЩЁ РАЗ О КОЛОДЦЕ ЛОТОСА // Старт в науке. 2021. № 1. ;URL: https://science-start.ru/ru/article/view?id=2047 (дата обращения: 05.03.2026).
