Изменения во всех сферах нашего общества обусловленные развитием цивилизации на рубеже XX – XXI веков привело к смене приоритетов в образовании. Это повлекло необходимость нового подхода к формированию нового специалиста-профессионала
Характерные черты профессионала нашего времени- творческая инициативность, самостоятельность , конкурентоспособность, мобильность. Эти черты необходимо развивать с самого детства. Формирование данных качеств приходится и на школьные годы. Именно в это время происходит основное развитие человека: ученик учится жить в обществе одноклассников, проявлять свою индивидуальность, отстаивать свои интересы, а также приобретает знания, развивает память, мышление, пространственное воображение и логику,
Однако, в настоящее время, интерес к образованию, изучению математики (в частности, геометрии), значительно упал.
Академик Александров А. Д. говорил о том, что задача геометрии – развить у обучаемых 3 качеств: пространственное воображение, практическое понимание и логическое мышление. Он ставил пространственное воображение на первое место не только в изучении геометрии, но и в большинстве видов человеческой деятельности [1,2].
В подготовке к ЕГЭ учитывается огромное количество разных факторов, влияющих на результат: объем знаний ученика, его физиологические особенности, особенности работы его памяти, внимания, пространственного мышления. В настоящее время в школьном систематическом курсе геометрии проводится разделение на планиметрию и стереометрию. Однако достаточное количество задач при подготовке к ЕГЭ содержат аналогичные свойства плоскости и пространства, значит, их решение можно рассматривать одновременно. Следовательно, проблема слитного изучения планиметрии со стереометрией очень актуальна в наши дни. Ведь, по сути дела, только в возрасте 15 лет наши дети, живущие в трехмерном пространстве, начинают его познавать с научной точки зрения. Слитное преподавание нескольких разделов математики, в том числе планиметрии и стереометрии называют фузионизмом (от латинского fusio (сплавление) или английского fusion – сплав металлов, слияние, соединение), именно так в 19-ом веке называли слитное преподавание различных школьных предметов.
Несмотря на явно нестандартный подход к преподаванию в сравнении к традиционной сложившейся системе- строго последовательного курса геометрии от планиметрии к стереометрии («Начала» Евклида),идеи фузионизма привлекали многих математиков. Фузионизмом были увлечены Ж.Даламбер (Д-Аламбер), Н.И.Лобачевский, Безу, Жергонн. Несмотря на большое значение фузионизма, в школе всё-таки не прижилось слитное преподавание планиметрии со стереометрией в систематическом курсе геометрии. Основная причина заключается в том, что фузионизм противоречит основным дидактическим принципам: от простого к сложному, последовательности, систематичности. Можно сделать вывод, что метод фузионизма будет весьма полезен и эффективен при проведении заключительного этапа изучения школьного курса геометрии – повторении основного пройденного материала, подготовке к ЕГЭ [5].
Геометрия на ЕГЭ — это четыре задачи в части В (две по планиметрии и две по стереометрии), а также задача С2 и С4. Как же научиться их решать? Прежде всего, при изучении планиметрии стоит смело обращаться к стереометрии. Так, например при решении задач из темы теорема косинусов можно находить не только элементы планиметрии
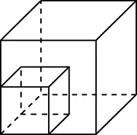
(В треугольнике АВС сторона АВ равна 13 см, сторона ВС равна 1 см. Угол С равен 150 градусам. Найти площадь треугольника АВС), но и неизвестные элементы фигур из стереометрии (В параллелепипеде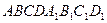
.BD=5,B
=6,?
=6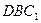0°.Найти
).
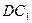Рассмотрим некоторые задачи из планиметрии и стереометрии, обладающие аналогичными свойствами [3,4].
|
Планиметрия |
Стереометрия |
|
Радиус вписанной в квадрат окружности равен 5. Найти площадь квадрата
|
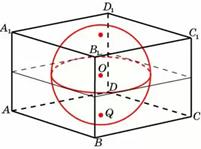
Радиус вписанной в куб сферы равен 1. Найдите его объем.
|
|
Диагональ квадрата равна 1.Найти площадь квадрата
|
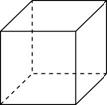
Диагональ куба равна 1. Найдите площадь его поверхности.
|
|
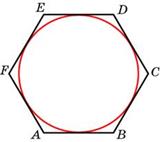
Найдите периметр правильного шестиугольника, если радиус вписанной окружности равен
|
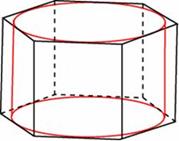
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2
|
|
Во сколько раз увеличится площадь квадрата, если все его стороны увеличить в три раза?
|
Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в три раза |
При изучении геометрических фигур следует опираться на основные дидактические блоки:
1)куб-квадрат
2)параллелепипед-прямоугольник
3)пирамида-треугольник
4)сфера-окружность.
Какой будет методика применения принципов фузионизма в школьной геометрии, ещё неясно, но уже сейчас понятно, что нельзя игнорировать исторический опыт решения данной проблемы. Поэтому следует на уроках геометрии при изучении планиметрических вопросов использовать стереометрический материал, либо параллельно с традиционным курсом планиметрии проводить элективные курсы, факультативные и кружковые занятия по стереометрии, значительно расширяющие круг изучаемых фигур и их свойств.
Библиографическая ссылка
Колузанова Т.Н. ФУЗИОНИЗМ И ЕГЭ // Старт в науке. – 2021. – № 2. ;URL: https://science-start.ru/ru/article/view?id=2030 (дата обращения: 19.04.2024).