Введение
Основная проблема исследования: показать красоту математических рисунков.
Актуальность темы исследования.
На самом деле наряду с развитием техники наблюдается тенденция к снижению уровня интеллектуального потенциала человечества. Развитие информационных технологий и гаджетов привело к тому, что количество думающих людей стремительно уменьшается, а количество ленивых людей растет. Мы уже не хотим считать в уме, потому что у нас есть калькулятор, Мы не хотим мыслить, потому что за нас это делает Интернет, мы не хотим делать некоторых обыденных вещей, так как за нас это могут сделать электронные устройства и гаджеты. Поэтому я решила наглядно показать красоту математического мира, и таким образом попытаться привлечь своих сверстников к изучению математики.
Цель исследования: выяснить существует ли взаимосвязь между математикой и живописью.
Задачи исследования: привлечь школьников к изучению математики.
Предмет исследования: теорема Вороного, правило золотого сечения, компьютерная графика, нетрадиционная техника рисования
Гипотеза: можно ли основываясь на математических расчетах и применении математических формул создавать рисунки.
Основная часть проекта.
В ходе изучения данного вопроса я изучила историю математики. Рассмотрела различные способы создания математических рисунков. Выяснила, что для создания рисунков можно применять компьютерные программы. Поняла, что любой рисунок можно разбить на геометрические фигуры и наоборот с помощью геометрических фигур можно создавать шедевры живописи. Для того, чтобы уметь создать правильные формы рисунка необходимо проводить специальные математические расчеты.
Проводя свое исследование я получила наслаждение мышлением и сделала выводы о том, что с помощью математических формул можно создавать различные математические рисунки, я узнала много интересного о знаменитых математиках которые, смогли доказать красоту математики в целом. А многочисленные способы создания математического рисунка вдохновили меня на дальнейшее исследование данной темы и создание рисунков с использованием компьютерных технологий. Поэтому в дальнейшем я обязательно изучу все компьютерные программы, а может создам и свою.
Математика – это уникальное средство познания красоты.
В наслаждении красотою есть элемент наслаждения мышлением.
Аристотель
Математика – это не только стройная система законов, теорем, задач, но и уникальное средство познания красоты. Изучая математику, мы открываем всё новые и новые слагаемые красоты, приближаясь к пониманию, а затем и к созданию красоты и гармонии.
Когда раскрывается эффективность применения математических методов в различных областях науки, культуры, искусства, не ущемляется роль математики, не подменяется другими предметами, а, наоборот, повышается интерес к предмету, выявляется высокое значение математики, процесс познания её делается увлекательным.
“Красота — первая проверка: в этом мире нет своего места для уродливой математики’’, — написал британский специалист по теории чисел Годфри Харди в 1941 году.
Чтобы ощутить вкус математической красоты, начну, скажем, со стакана с холодной газировкой. Поставлю его на матовую бумагу в три разных места так, чтобы отпечатались три окружности, позаботившись при этом, чтобы все эти три окружности пересеклись в одной точке. Теперь вопрос: насколько большим должен быть один стакан, чтобы охватывать три другие точки пересечения? Кто-нибудь почти всегда предполагает, что только очень большой стакан можно так поставить. А правильный ответ удивляет: нужен такой же стакан! Это совершенно верное решение. Эта теорема была опубликована Роджером А. Джонсоном в 1916 году. Теорема Джонсона об окружности демонстрирует два из основных требований к математической красоте. Во-первых, это удивительно. Окружность того же размера неожиданно возникает в решении. Во-вторых, это просто. Математические понятия, окружности и радиусы, являются базовыми, выдержавшими испытание временем.
А, например, теорема геометризации Григория Перельмана утверждает, что большинство вселенных имеет естественную геометрическую структуру, отличную от той, которую мы изучаем в средней школе. Согласно теореме Перельмана, наша видимо плоская Вселенная представляет собой удивительное исключение. Очевидно, что для Перельмана изменение наших представлений о Вселенной было ему достаточной наградой.
Математика и дизайн.
Незадолго до своей смерти в 1908 году, российский математик украинского происхожденияГеоргий Вороной описал очень интересныйметод разбиенияпространства для многомерного случая. Диаграммы Вороного нашли применение в десятках областей деятельности человека: компьютерное моделирование, физиология, робототехника, металлургия, вычислительная химия, кристаллография, биология, зоология, антропология, экология, астрономия, картография, маркетинг, логистика и т. д. Красота и гармония диаграмм Вороного не остались незамеченными архитекторами и дизайнерами всего мира. Различныеарт–объекты,мебельи другие интерьерные решения впечатляют. Впечатляют и результаты работы с применением среды графического редактораRayFire. Будучи одним из самых совершенных представителей ПО, основанного на алгоритме разбиения Вороного, а также его вариациях, RayFire использовался ведущими CGI–студиями для работы над такими голливудскими блокбастерами, как «Железный человек» (2008 г.), «Мстители» (2012 г.) и др., а также во множестве игровых проектов. [7]
Что такое диаграммы Вороного
Это разбиение метрического пространства на области, в которых находятся объекты, таким образом, что каждому объекту соответствует область пространства, образованная точками, которые находятся ближе к этому объекту, чем к любому другому. Это свойство диаграммы Вороного имеет непосредственные приложения, такие как поиск “ресторана’’ быстрого питания известной сети ресторанов, наиболее близкого к вам, к примеру, если вы путешествуете по Парижу. И хотя моя работа с диаграммами Вороного связана с вычислительной геометрией, относительно молодой дисциплиной, некоторые авторы говорят, что эту структуру использовал в 1644 году Декарт в своих работах по астрономии, когда утверждал, что Вселенная заполнена эфиром и материей и образована вихрями.
Без сомнения, с исторической точки зрения достойное упоминания применение диаграммы Вороного появилось в работах Джона Сноу, которого многие считают отцом современной эпидемиологии, исследовавшего холеру, поразившую Лондон в 1854 году.
Сноу с помощью географического метода выявил, что причиной болезни было употребление воды, загрязненной фекалиями. Для этого он нанес на карту распределение смертей от холеры. Затем он изучил расположение источников питьевой воды в городе и определил области Вороного для каждого из них. Рассчитав расстояния между местом жительства каждого погибшего и ближайшей водокачкой, он сделал вывод, что район, наиболее сильно пострадавший от холеры, соответствует области Вороного, связанной с водокачкой на Брод-стрит (Broad street), так как здесь умерло 73 из 83 человек. После удаления ручки этой водокачки вспышка холеры была погашена. С тех пор и до сегодняшнего дня диаграммы Вороного в двух и трех измерениях использовались в самых разных областях. Например, в робототехнике, если у нас есть местность с препятствиями, по которой должен двигаться робот, возможно избежать столкновений, если разработать траекторию робота так, чтобы она проходила по линиям диаграммы Вороного для препятствий, которые будут находиться всегда на полпути между каждыми двумя из них. Та же самая стратегия может быть использована в дипломатии для лавирования между конкурирующими интересами. [1]
Содержание исследования.
Вдохновившись этими интересными знаниями я поняла, что все, что вы хотите нарисовать, можно разбить на простые фигуры. Изобразить их несложно. Прорисовывая поверх геометрических фигур желаемую картину, вы получите правильные пропорции. Если же нужно рисовать в объеме, помогут геометрические тела – цилиндр, конус, шар и другие. Композиция картины также вписывается в ту или иную фигуру. [6]
Ось мира
Не обойтись в живописи без осевых линий. Они нужны, чтобы обозначить местоположение лепестков у цветка, для рисования портрета.
Мозаика, узор, орнамент
Мозаика представляет собой кусочки материала, которыми выкладывается поверхность. Как правило, кусочки бывают разноцветными и образуют рисунок или узор. Сложность мозаики не только в выкладывании рисунка, требуется, чтобы между кусочками не оставалось зазоров, и они не перекрывали друг друга.
Золотое сечение
В 1509 году в Италии появилась книга Луки Пачоли под названием «О божественной пропорции». В ней были установлены математические соотношения, соблюдая которые художник достигнет красоты. Иллюстрации - 60 многогранников и рисунок «Витрувианский человек» принадлежали руке Леонардо да Винчи. Еще одна идеальная пропорция тела была сформулирована еще во времена Древней Греции:
Рост человека=размаху рук (от кончиков пальцев) =8 ладоням=6 ступням=8лицам
ЗАДАЧА: Попробуй проверить эту формулу на себе.
Я проверила эту формулу на своих одноклассниках. Оказалось, что идеальные пропорции имеют 80% класса. Значит, все-таки она не идеальна, так как о ней говорят.
У золотого прямоугольника есть одно замечательное свойство. Если отсечь от него квадрат, останется тоже золотой прямоугольник. Портрет Моны Лизы, написанный Леонардо да Винчи, построен на золотом сечении, ее лицо вписано в золотые прямоугольники разного размера. В «Тайной вечере» золотые прямоугольники определяют размеры картины и положение ее персонажей. [1]
По правилу золотого сечения строят не только прямоугольники, но и любые другие фигуры, в том числе пятиконечную звезду и многогранники.
Фантастические картины из математических формул
Это замечательные работы итальянки Сильвии Кордедды (Silvia Cordedda).
Все творения – это фрактальная графика, молодой, но бурно развивающийся вид компьютерной графики. Безусловно, рисунок, описанный математической формулой, создает компьютер, но подбирает параметры формулы и таким образом определяет конечный вариант изображения все же человек. [6]
Математическое рисование. Рисование прямыми линиями
Мозг человека хорошо воспринимает узоры и ритм, на которых основана и математика, и изобразительное искусство. Когда наша фантазия оживляет числа и фигуры, начинаются настоящие чудеса. Чтобы изображать кривые, не нужны окружности. Кривые можно получить из прямых!
Математика - это очень красивая наука! Предлагаю вам провести несложный эксперимент, чтобы вы в этом убедились. Прямыми линиями можно рисоватьнеобыкновенно красивые изображения. А как интересно придумывать узоры для таких изображений!  Эта идея лежит в основе популярной техники вышивки, которая называется изонить.
Эта идея лежит в основе популярной техники вышивки, которая называется изонить.
Это медитативное расслабляющее занятие занимательной математикой и нетрадиционной техникой рисования одновременно способно увлечь не только детей, но и взрослых.[4]
Стомахион
Стомахион — это старинная головоломка, в которой нужно правильно сложить 14 элементов, чтобы получить изображение животного, растения или предмета. Переведите эти фигуры на лист бумаги и вырежите их. А теперь попробуйте сложить из них синего слона и красного робота. Соберите из деталей квадрат и треугольник как можно большим количеством способов. [3]
Мыльные пузыри
В ограниченное пространство можно поместить бесконечное множество кругов. В треугольник нужно самую большую окружность, какую только возможно. А затем заполнить оставшиеся места окружностями, рисуя каждый раз окружность с максимально большим радиусом. Окружности должны касаться друг друга или сторон треугольника, но не пересекаться. [2]
Практическая часть
Для меня владение рисунком доставляет много радости, открывает мир красоты, делает жизнь ярче.
Прежде всего, я научилась:
1. видеть реальные предметы так, словно вы рассматриваете готовый рисунок. Замечать, как меняется вид предмета при перемене места, с которого на него смотрят. Обращать внимание, как меняется окраска предметов при изменении освещения.
2. Обращать внимание на соотношение размеров и пропорций.
3. Хорошо рисовать пейзажи.
4. Сочинять рисунки по собственному замыслу.
Математика в школе мне показалась скучным предметом. Однако начав изучать геометрию поняла, что с помощью геометрических фигур можно создавать красивые рисунки. Решила выяснить, а можно ли на самом деле создавать рисунки, основываясь на математических знаниях и настолько ли они красивы, как о них говорят. Проведя исследование математических рисунков, я решила сама попробовать применить предложенные способы, решая следующие практические задачи.
Результаты, полученные в ходе исследований.
Вдохновившись этими интересными знаниями и вооружившись необходимыми принадлежностями для рисования я написала следующие картины.
Задача 1: разбей альбомный лист по правилу золотого сечения и нарисуй простой пейзаж.

Задача 2: придумайте собственные необыкновенные узоры из прямых линий.

Задача 3: мыльные пузыри.
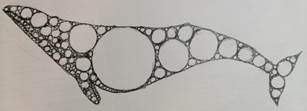
Задача 4: разбить картинку на различные фигуры.

Задача 5: интерактивный конструктор - мой дизайн от Вороного [8].

Выводы:
Проводя свое исследование сделала выводы о том, что с помощью математических формул можно создавать различные математические рисунки, я узнала много интересного о знаменитых математиках которые, смогли доказать красоту математики в целом.
Заключение.
Многочисленные способы создания математического рисунка вдохновили меня на дальнейшее исследование данной темы и создание рисунков с использованием компьютерных технологий. Поэтому в дальнейшем я обязательно изучу все компьютерные программы, а может, создам и свою.
Библиографическая ссылка
Крикунова А.А. КРАСОТА МАТЕМАТИЧЕСКИХ РИСУНКОВ // Старт в науке. 2021. № 2. ;URL: https://science-start.ru/ru/article/view?id=2028 (дата обращения: 03.03.2026).
