• Авторы
• Научный руководитель
• Файлы
• Ключевые слова
• Литература

Санникова А.А. 1

---

1 "МБОУ СОШ № 10" города Елабуги Республики Татарстан

Санникова Галина Ивановна (г.Елабуга, МБОУ «Елабужская средняя общеобразовательная школа № 10»)

Статья в формате PDF

291 KB

логика

логическое мышление

граф

1. Игнатьев Е.И. В царстве смекалки

2.Логические задания для 1 - 5 класса. Издательство «Феникс». Ростов на Дону, 2015 г.

3.Удодова Н.И. Занимательная математика: смекай, считай, отгадывай. – Издательство «Учитель», 2011 г.

4.Фокин Б.Д. Арифметика: сборник занимательных задач/ Б.Д.Фокин. – М.: АРКТИ, 2001 г.

5. Нагибин, Ф.Ф. (Киров). Применение Графов для решения логических задач. // Математика в школе. – 1964. - № 3.

6.Нагибин, Ф.Ф., Канин, Е.С. Математическая шкатулка: Пособие для учащихся 4-8 кл. сред. шк. – 5-е изд. – М.: Просвещение, 1988.

7. Шевченко, В.Е. Логические задачи. - К., 1979.

8. Интернет-ресурсы: http://wiki.iteach.ru; http://dic.academic.ru

… Всякая задача кажется очень простой после того, как вам её растолкуют.
Шерлок Холмс

Введение

Логические задачи от обычных отличаются тем, что не требуют вычислений, а решаются с помощью рассуждений. Можно сказать, что логическая задача – это особая информация, которую не только нужно обработать в соответствии с заданным условием, но и хочется это сделать. Эти задачи носят занимательный характер и не требуют большого запаса математических знаний, поэтому они привлекают даже тех учащихся, которые не очень любят математику. Только решение трудной, нестандартной задачи приносит радость победы. При решении логических задач предоставляется возможность подумать над необычным условием, рассуждать. Это у меня вызывает и сохраняет интерес к математике. Логически обоснованное решение – лучший способ раскрытия творческих способностей. Я люблю решать нестандартные, занимательные, особенно логические задачи. А ведь с помощью логических задач развиваются воображение, логическое мышление, зрительная память, сила воли, творчество, терпение. Также это возможность проводить творчески свободное время на переменах, после уроков и надолго решить проблему семейного досуга с пользой для всех.

Математика – это царица всех наук. И это немудрено. Поскольку все точные науки сосредоточены на вычислениях. Однако это вовсе не означает, что всё в этом царстве скучно. Многие считают, что математика это скучная, трудоёмкая работа. Но на самом деле это не так! В своей работе я докажу, что математика очень увлекательная, занимательная наука. Изучая математику можно весело и интересно провести время, узнав много нового и интересного. «Предмет математики настолько серьезен, что нужно не упустить случая, сделать его немного занимательным» - это высказывание принадлежит выдающемуся французскому математику Блезу Паскалю. Решать логические задачи очень увлекательно. В них вроде бы нет никакой математики - нет ни чисел, ни геометрических фигур, а есть только лжецы и мудрецы, истина и ложь. В то же время дух математики в них чувствуется ярче всего - половина решения любой математической задачи (а иногда и гораздо больше половины) состоит в том, чтобы как следует разобраться в условии, распутать все связи между объектами задачи.

Гипотеза (ожидаемые результаты): логические задачи расширят круг моих интересов.

Актуальность исследования: решение логических задач развивает память, воображение, находчивость, сообразительность, логическое мышление, наблюдательность, помогает усваивать предметы математического цикла и подготовиться к олимпиадам.

Исследуемая проблема: действительно ли логические задачи могут стать достойной заменой гаджетов для меня? И улучшится ли у меня успеваемость по математике?

Объект исследования: является ли решение логических задач, как способ интеллектуального развития без использования электронных гаджетов. Цель :выявить умения рассуждать и делать правильные выводы, при решение логических задач.

Задачи: ознакомление с понятиями «логика» и «математическая логика»; изучение основных типов логических задач; научиться решать логические задачи для 5 класса.

Что такое логика и логические задачи

Слова «логика» означает совокупность правил, которым подчиняется процесс мышления. Сам термин «логика» происходит от древнегреческого «logos», означающего «слово, мысль, понятие, рассуждение закон». Логика - одна из древнейших наук.

Уже с этих времен было принято считать, что логика есть наука о мышлении, а не о предметах объективной истинности. В научной литературе можно найти следующие определения логики. Логика - наука о приемлемых способах рассуждения. Логика - наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Логика - наука о правильном мышлении. Логика - одна из древнейших наук. Отдельные истоки логического учения можно обнаружить еще в Индии, в конце II тысячелетия до н. э Основоположником логики как науки является древнегреческий философ и ученый Аристотель. Именно он обратил внимание на то, что в рассуждениях мы из одних утверждений выводим другие, исходя не из конкретного содержания утверждений, а из определенной взаимосвязи между их формами, структурами.

Решение задач - это практическое искусство; подобно плаванию, катанию на лыжах или игре на фортепиано, научиться ему можно, только подражая хорошим образцам и постоянно практикуясь. При этом каждая задача неизменно заканчивается вопросом, на который надо дать ответ. Задача пробуждает мысль человека активизирует его мыслительную деятельность. Решение задач по справедливости считается гимнастикой для ума.

Как научиться решать логические задачи?

Логические или нечисловые задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной). Итак, мы узнаем, как разными способами можно решать логические задачи. Оказывается таких приемов несколько, они разнообразны и каждый из них имеет свою область применения.

Типы логических задач:

1. Задачи с отношениями (решение нескольких задач рассмотрено очень подробно).
2. Задача с использованием схем и таблиц
3. Задача на переправу
4. Задача, решаемая с помощью графов.
5. Задача на перебор возможных вариантов.
6. Занимательные задачи.

Как правило, при решении задачи могут быть выделены следующие этапы.

1. Анализ условия задачи (выделение исходных данных).
2. Поиск метода решения.
3. Символическая запись задачи.
4. Рассуждения и пояснения к решению
5. Анализ полученных результатов и запись ответа.

Задачи с отношениями

Необходимым условием успешного решения логических задач с транзитивными отношениями: «больше», «меньше», «равно» и другими является умение перейти от отношений разного вида между элементами задачи к отношениям одного вида. Например, если в задаче встречаются отношения «легче» и «тяжелее», то надо заменить отношение «легче» отношением «тяжелее» с соответствующей перестановкой исходных данных.

Кроме того, для решения задачи необходимо умение моделировать ее с помощью схемы, т. е. записывать словесное условие задачи в виде модели­ иллюстрации. Начать решение задачи можно как раз с рассмотрения модели-иллюстрации.

Задача 1. Что тяжелее всего?

Груша тяжелее яблока, а персик легче яблока. Какой из фруктов самый тяжелый?

Решение. Ученики проговаривают условие задачи и записывают его в тетрадь. Дано: Яблоко (Я), Груша (Г) ,Персик(П).

Рассуждения: гяяп, гяп

Ответ: груша тяжелее всех фруктов

Задача 2. Кто старше всех? Три брата - Ваня, Саша, Коля - учатся в разных классах одной школы. Коля старше Вани, а Саша моложе Вани. Назовите имена старшего, среднего и младшего братьев.

Ответ: Коля - старший брат, Ваня - средний, Саша - младший.

Задача 3. Цветные карандаши

У Пети три карандаша - желтый, коричневый и черный. Назовите самый короткий и самый длинный карандаши, если известно, что:

а) желтый карандаш короче коричневого, а черный - короче желтого;

б) желтый карандаш длиннее черного, а коричневый короче черного.

Ответ: а) коричневый карандаш - самый длинный, черный - самый короткий; б) желтый карандаш - самый длинный, коричневый - самый короткий.

Задачи с использованием схем и таблиц

Задача 4. Спортивные соревнования. Коля, Боря, Вова и Юра заняли первые четыре места в спортивном соревновании. На вопрос, какие места они заняли, они честно ответили:

-Коля не занял ни первое, ни четвертое место;

-Боря занял второе место;

-Вова не был последним.

Какое место занял каждый мальчик?

Решение: 1. По условию задачи известно, что Боря был вторым, все остальные ячейки этой строки и столбца заполняем нулями «крестом»:

2. Так как Коля не занял ни первое, ни четвертое место (по условию) и не занял второе место, которое занял Боря (по условию), он занял третье место. Ставим в ячейку «Коля, 3» цифру 1. Значит, Вова и Юра не могут занимать третье место. Ставим в ячейки «Вова, 3», «Юра, 3» цифру 0:

3.Так как Вова не занял четвертое место (по условию), не занял второе место, так как его занял Боря (по условию), и не занял третье место (по доказательству), он занял первое место, а Юра - четвертое. Ставим в ячейку «Вова, 1» цифру 1, в ячейку «Юра, 1» - цифру О, а в ячейку «Юра, 4» - цифру 1) :

Ответ: в соревнованиях Вова занял первое место, Боря - второе, Коля - третье, Юра – четвертое.

Задачи на переправу

Трудность задач на переправу связана с ограниченной грузоподъемностью плавательных средств в условиях задач и с количеством и особенностями пассажиров. Для записи хода решения таких задач используют схему, которую предлагается составлять следующим образом: схематично изображаются река, берега и плавательное средство; каждый этап переправы отделяется горизонтальной чертой; направление движения плавательного средства указывается стрелкой над обозначениями тех, кто переправляется на текущем этапе. Запись хода решения задачи в виде схемы способствует повышению интереса ребят, помогает детям представить содержание задачи и, что самое главное, содействует осмысленному пониманию хода рассуждений.

Задача 5. Поход.

Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться на другой берег отцу и сыновьям? Сколько времени (минимально) потребуется на переправу, если Каждая поездка через реку занимает 3 минуты?

Дано: Первый сын (Cl) Второй сын (С2) Отец(О) Как переправиться?

Решение.

Ответ: на переправу потребуется: 15 минут

Задачи, решаемые с помощью графов.

Приведенная ниже задача решается с помощью графа: в ходе решения задачи вычерчивается граф - фигура, состоящая из отдельных вершин, соединенных друг с другом.

Задача 6. Игрушки.

У Юры два автомобиля, четыре медвежонка и три мяча. Он хочет выбрать из этих игрушек один автомобиль, одного медвежонка и один мяч. Сколько у него есть вариантов выбора?

Решение.

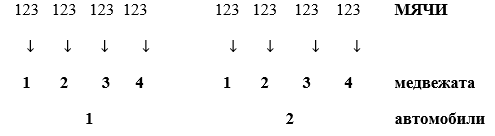
2×4×3=24

Ответ: 24 варианта.

Задачи на перебор всевозможных вариантов.

Задачи на перебор возможных вариантов решаются следующим образом: выдвигается некая гипотеза, которая подтверждается или опровергается в ходе дальнейших рассуждений. Гипотезы выдвигаются до тех пор, пока не найдется единственный истинный вариант.

Задача 7 Необычная тетрадь

Однажды на лестнице была найдена странна.я: тетрадь. В ней было записано 100 утверждений: «В этой тетради ровно одно неверное утверждение». «В этой тетради ровно два неверных утверждения:». «В этой тетради ровно три неверных утверждения» … … … «В этой тетради ровно сто неверных утверждений». Есть ли среди этих утверждений верные и если да, то .какие?

Решение.

Каждые два утверждения: в этой тетради противоречат друг другу. А это означает, что если в ней и найдется верное утверждение, то оно будет единственным. Если верно только одно какое-то утверждение, то девяносто девять ложны. И такое утверждение есть: «В этой тетради ровно девяносто девять неверных утверждений».

Ответ: верное утверждение «В этой тетради ровно девяносто девять неверных утверждений».

Занимательные задачи.

Существует множество занимательных задач, которые достаточно быстро и легко можно решить с помощью рисунков, таблиц, схем и т.д.

Задача7. Из гнезда вылетели три ласточки. Какова вероятность того, что через 15 секунд они будут находиться в одной плоскости?

(Ответ: 100%, так как три точки всегда образуют одну плоскость)

Задача8. На столе лежат две монеты, в сумме они дают 3 рубля. Одна из них — не 1 рубль. Какие это монеты?

(Ответ: 2 рубля и 1 рубль. Одна то не 1 рубль, а вот другая — 1 рубль)

Задача9. С какой скоростью должна бежать собака, чтобы не слышать звона сковородки, привязанной к ее хвосту?

(Ответ: Если выдумаете, что ей нужно бежать со сверхзвуковой скоростью, то вы ошибаетесь — собаке достаточно стоять на месте)

Задача10. Один оборот вокруг Земли спутник делает за 1 ч 40 мин, а другой — за 100 минут. Как это может быть?

(Ответ: 1 ч 40 мин = 100 мин)

Задача11. Крыша одного дома несимметрична: один скат ее составляет с горизонталью угол 60 градусов, другой — угол 70 градусов. Предположим, что петух откладывает яйцо на гребень крыши. В какую сторону упадет яйцо — в сторону более пологого или крутого ската?

(Ответ: Петухи не кладут яйца)

Задача 12. В 12-этажном доме есть лифт. На первом этаже живут всего 2 человека, от этажа к этажу количество жильцов увеличивается вдвое. Какая кнопка в лифте этого дома нажимается чаще других?

(Ответ: Независимо от распределения жильцов по этажам, кнопка «1»)

Задача 13.В двух кошельках лежат две монеты, причем в одном кошельке монет вдвое больше, чем в другом. Как такое может быть?

(Ответ: Один кошелек лежит внутри другого)

Задача14. Сын отца профессора разговаривает с отцом сына профессора, причем сам профессор в разговоре не участвует. Может ли такое быть?

(Ответ: Да, может, если профессор — женщина)

Задача15. Если в 11 часов ночи идет дождь, то возможно ли через 48 часов солнечная погода?

(Ответ: Нет, так как будет ночь)

Задача16. Летели скворцы и встретились им деревья. Когда сели они по одному на дерево, то одному скворцу не хватило дерева, а когда на каждое дерево сели по два скворца, то одно дерево осталось незанятым. Сколько было скворцов и сколько деревьев?

(Ответ: Предположим, что после того как скворцы сели на деревья по два, с каждого дерева взлетело по одному скворцу. Один из взлетевших скворцов может сесть на незанятое дерево, тогда на каждом дереве будет сидеть по одному скворцу. По условию, если на каждое дерево сядет по одному скворцу, то один скворец останется в воздухе. Значит, взлетело 2 скворца. Тогда общее число скворцов равно 4, а число деревьев З).

Заключение

В данной работе вы познакомились с логическими задачами. Вашему вниманию были предложены различные типы логических задач.

Решение логических задач – это не только очень увлекательный, но и крайне полезный способ времяпрепровождения, как для школьников, так и для взрослых. Логические задачи – это хороший способ развития умственных способностей для школьников всех возрастов. Логические или нечисловые задачи составляют обширный класс нестандартных задач. Люди, способные принимать нестандартные решения и умеющие логически мыслить необходимы обществу. Также я считаю, что логика помогает нам в нашей жизни справиться с любыми трудностями, и все что мы делаем, должно быть логически осмысленно и построено. Поэтому я выбрала эту тему : «Логические задачи». Над этой проблемой продолжу работу: буду изучать литературу, предлагать нестандартные задачи одноклассникам, буду готовиться к олимпиадам по математике.

Библиографическая ссылка