• Авторы
• Научный руководитель
• Файлы
• Литература

Габова Е.Н. 1

---

1 аул Катанов, МБОУ Катановской средней общеобразовательной школы, 9 класс

Габова А.Н. (аул Катанов, МБОУ Катановской средней общеобразовательной школы)

Статья в формате PDF

3381 KB

1. Касьянов В.А. Тетрадь для лабораторных работ по физике, 10 класс. № 8622 / 0790 – Дрофа, 2004.

2. Никитин А.А. Геометрия 8-9 классы НГУ. № 8622 / 0790 – Новосибирск, 2000.

3. Перышкин А.В. Физика 7-9. № 8622 / 0790 – Дрофа, 2014.

4. Савченко О.Я. Физика в № 8622 / 0790 задачах НГУ СУНЦ НГУ. № 8622 / 0790 – Новосибирск, 2013.

5. Федотович Г.В. Экспериментальные работы по физике Социализированный учебно-научный центр НГУ. № 8622 / 0790 – Новосибирск, 2014.

6. URL: https://ru.wikipedia.org/wiki/Чёрный_ящик.

Эта работа интересна тем, что рассматривая олимпиадные задания по физике, приходится решать задачи различной степени трудности от почти стандартных до сравнительно сложных, требующих смекалку, глубокие знания, умения ориентироваться в непривычной или усложненной ситуации.

При подготовке к «Всесибирской открытой олимпиаде по физике », её организаторами были предложены экспериментальные задачи, одна из них нас заинтересовала, её решение потребовало создать модели установок, выполнить экспериментальные измерения, проанализировать результаты, сделать заключительные выводы.

Черный ящик

Чёрный ящик – термин, используемый для обозначения системы, внутреннее устройство и механизм работы которой очень сложны, неизвестны или неважны в рамках данной задачи. «Метод чёрного ящика» – метод исследования таких систем, когда вместо свойств и взаимосвязей составных частей системы, изучается реакция системы, как целого, на изменяющиеся условия. Подход чёрного ящика сформировался в точных науках (в кибернетике, системотехнике и физике) в 20-40 годах XX века и был заимствован другими науками (прежде всего, бихевиористической психологией).

Рис. 1. Чёрный ящик, вход и выход

Модель чёрного ящика

Система, которую представляют как «черный ящик», рассматривается как имеющая некий «вход» для ввода информации и «выход» для отображения результатов работы, при этом происходящие в ходе работы системы процессы наблюдателю неизвестны. Предполагается, что состояние выходов функционально зависит от состояния входов.

Каноническое представление чёрного ящика – это полное описание его функций. Два черных ящика с одинаковыми каноническими представлениями считаются эквивалентными.

Изучение системы по методу чёрного ящика сводится к наблюдениям за ней и проведению экспериментов по изменению входных данных, при этом в ходе наблюдения над реакциями системы на внешние воздействия достигается определённый уровень знаний об исследуемом объекте, позволяющий осуществлять прогнозирование поведения «чёрного ящика» при любых заданных условиях.

Применимость метода

Примером применения метода чёрного ящика является исследование многополюсника, устройство которого неизвестно или бихевиористический подход к эксперименту и его интерпретация в психологии.

Знания, полученные об объекте по методу чёрного ящика, не позволяют получить информацию о его внутреннем строении.

Данный метод применяется для решения задач моделирования управляемых систем, в инженерной психологии – для формального описания деятельности оператора и построения её математических моделей.

Задание. Известно, что внутри «черного ящика» находится несколько вставок с вертикальными вырезами квадратного сечения (см. рисунок). Найдите длину стороны выреза а, и высоту h, каждой вставки, начиная с уровня, на котором в коробку вставлена трубочка. Предложите метод её решения. Проделайте измерения повторно. Оцените точность измерения.

Оборудование. «Черный ящик со вставками», сосуд с водой, соломинка из под коктейля, миллиметровка, шприц [5 ст. 22].

Цель исследовательской деятельности: экспериментальным методом выяснить геометрические размеры и формы физических тел, находящихся в «черном ящике».

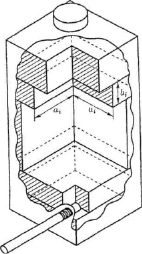
Рис. 2

Задачи:

- Изучить теорию используемых законов из физики и математики;

- Освоить метод решения поставленной цели;

- Создать модели исследуемых установок;

- Проделать измерения, построить графики процессов, проанализировать их;

- Провести алгебраическое и арифметическое решение задач;

- Определить геометрические размеры и формы физических тел находящегося в «черном ящике»

- Заключение: провести сравнительный анализ и сделать выводы.

В работе применяю эмпирические методы исследования процессов: эксперимент, наблюдение, анализ, синтез, сравнение, обобщение.

Гипотеза исследования: если применить «Метод чёрного ящика» к выбранным моделям, то можно определить геометрические размеры и формы физических тел находящегося в ящике, без визуального их восприятия.

Теоретическая часть

Физические и математические законы используемые в работе

Закон сообщающихся сосудов: свободный уровень однородной жидкости во всех коленах сообщающихся сосудов одинаковый относительно поверхности земли.

Закон Архимеда: Тело полностью погруженное в жидкость вытесняет жидкость такого же объёма и вес этой жидкости равен силе Архимеда

Vт = Vж

Fa = ж•g•Vж

Математические законы:

Объём параллелепипеда:

V = а·b·c

Объём куба: V = a³

Объем шара: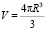

Диаметр: d = 2·R

Тангенс угла наклона: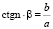

Погрешности при прямых измерениях физической величины

Точность результата прямого однократного измерения значения физической величины невелика вследствие двух погрешностей, которые невозможно полностью исключить в процессе опыта, – это случайная и грубая погрешности.

Случайная погрешность – погрешность, изменяющаяся случайным образом при повторных измерениях. Она вызывается непостоянством внешних условий и несовершенными действиями экспериментатора.

Грубая погрешность (промах) – погрешность, существенно превышающая ожидаемую при данных условиях. Грубая погрешность обусловлена ошибочным отсчетом или временной неисправностью измерительного прибора.

Для уменьшения влияния случайных факторов проводят многократные измерения данной физической величины alt a2, ..., ап. При этом результаты измерений, содержащих промахи, исключаются из дальнейшей обработки результатов.

В качестве действительного значения физической величины принимают среднее арифметическое значение измеряемой величины

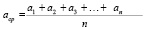
где п – число измерений.

Рассмотрим один из возможных вариантов измерений, когда проводят пять измерений случайной величины (п = 5).

Случайную погрешность асл (или погрешность среднего арифметического) оценивают как средний модуль отклонения результатов измерений от среднего арифметического значения аср:

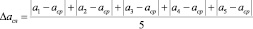
Результирующая абсолютная погрешность при прямых измерениях физической величины а учитывает как приборную aпр, так и случайную aсл погрешность и находится как их сумма:

a = aсл +aпр

Значение физической величины, полученное в результате прямого измерения, записывают в виде a = a ± a

Относительная погрешность при прямых измерениях – безразмерная физическая величина, равная отношению абсолютной погрешности к среднему арифметическому значению измеряемой величины: [1 ст. 5]

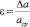
Метод решения поставленной цели

Система, которую представляют как «черный ящик», рассматривается как имеющая некий «вход» для ввода информации и «выход» для отображения результатов работы, при этом происходящие в ходе работы системы процессы наблюдателю неизвестны или частично неизвестны. Предполагается, что состояние выходов функционально зависит от состояния входов [6].

Краткое решение для достижения цели: будем по два (четыре или пять, шесть) кубика через крышку установки наполнять коробку водой и записывать в таблицу высоту столба жидкости в трубочке. На миллиметровке построим график высоты столба воды в коробке от количества налитой воды. Проведу объяснение полученный график. Используя полученные результаты, определите размеры вставок и создам геометрические образы вставок. Оценю точность измерения.

Практическая часть исследовательской деятельности

Модели исследуемых установок

Подручные материалы: коробка из под молока, цилиндры из под герметика и газировки, игрушки пластиковые трубки, миллиметровая бумага, шприц, вставки вырезаны из пенопласта, универсальный клей, теннисные шарики. Собрала установки которые изображены на рис. 2. Вставки вклеены во внутрь цилиндров и коробки. Сверху все установки закрыты, там имеется отверстие для вливания воды.

Рис. 4. Экспериментальные установки

Исследовательская деятельность

Исследовательскую деятельность провела по следующему плану:

1. Наполнять коробку водой по два (четыре или пять, шесть) кубика через крышку установки и записывать в таблицу высоту столба жидкости в трубочке.

2. На миллиметровке построить график высоты столба воды в коробке от количества налитой воды.

3. Анализировать полученные графики.

4. Используя полученные результаты, провести алгебраическое и арифметическое решение задач; определить размеры вставок.

5. Определить геометрические размеры и формы физических тел находящегося в «черном ящике»

6. Оценить точность измерения.

Примечание: чтобы понять механизм физических и математических зависимостей, исследование провожу со всеми сосудами, а в данном реферате представлю отчет по коробке «Весёлый молочник», цилиндру «Krass», игрушка – конус.

Задача № 1 Черный ящик с «Весёлым молочником»

Дано:

Коробка с вставками. Вставки прямоугольные параллелепипеды в двух нижних вырезки с квадратной формой у основания.

Вопросы: Сколько вставок? Каковы размеры и объёмы этих вставок? Каковы размеры и объёмы вырезки в каждой вставке? Представить рисунок вставки с вырезкой. Оценить точность измерений.

Рис. 5. Рабочий момент

Примечание: График программой Excel сильно сглажен, анализировать его сложно, для анализа воспользуемся графиками на миллиметровой бумаге.

Приложение № 1: График зависимости подъёма жидкости по капилляре от объёма вливаемой воды в сосуд «Весёлый молочник» (Опыт повторила трижды. Анализирую красный график процесса, остальные рассуждения и таблицы аналогичны).

Анализ красного графика: Первый способ рассуждений

1. Нижний график показывает зависимость высоты подъема жидкости в капилляре от объёма вливаемой жидкости в сосуд – эта зависимость прямая. Изломы верхнего графика говорят о том, что с этих точек начинается и заканчивается вставка и её вырезка. Таким образом в данном сосуде три вставки.

Так как это сообщающиеся сосуды то высота излома и есть высота вставки и «вырезки»:

H1 = 40мм – 5мм = 35мм

H2 = 85мм – 50мм = 35мм

H3 = 130мм – 100мм = 30мм

3. Найдём объём вырезанной части, которую заполнила вода для нижнего среднего и верхнего участка:

V1 = 80мл – 35мл = 45мл

V2 = 165мл – 145мл = 20мл

V3 = 350мл – 245мл = 105мл

4. Зная высоту и то, что в основании квадрат найдём сторону квадрата «вырезки»:

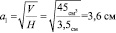
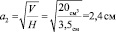
5. Найдём площадь основания коробки:

Sос = A2 = 7 см*7см = 49 см2

6. Найдём объём вставки:

Vвст = Sос* H – Vвырезки

Vвст1 = 49 см2* 3,5 см – 45 см3 = 147 см3 – 45 см3 = 102 см3

Vвст2 = 49 см2* 3,5 см – 20 см3 = 147 см3 – 20 см3 = 127 см3

Vвст3 = 49 см2* 3,5 см – 105 см3 = 147 см3 – 105 см3 = 32 см3

7. Для верхней вставки найдём площадь свободной воды так как вставка маленькая:

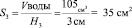
Sвставки 3 = Sосн – S3 = 49 см2 – 35 см2 = 14 см2

8. Найдём сторону верхней вставки:

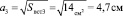
9. На какой высоте от основания находится каждая вставка:

h1 = 5мм

h2 = 50мм

h3 = 100мм

Анализ графика: Второй способ рассуждений

Рассмотрим геометрическую интерпретацию графика: [2 и 4]

= угол наклона графика ctan = площади вырезанной части

это следует из математической аналогии:

.

.

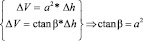
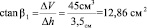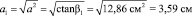
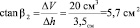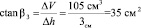
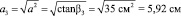
Дальнейшее решение аналогично первому.

Таблица 1

Рабочая таблица № 1

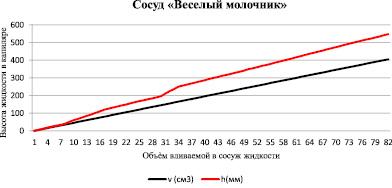
Рис. 6. Рабочий график

Таблица 2

Расчет погрешностей: прямых измеряемых величин

Таблица 3

Расчет погрешностей: косвенных расчетных величин

Выводы из решения задачи:

а) Параметры вставок:

Нижняя вставка: Vвст1 = 102 см3

Высота: H1 = 35мм

Сторона вырезанного квадрата:

a1 = 3,46 см (реально 3 см)

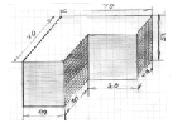
Рис. 7. Геометрический вид вставки

Средняя вставка:Vвст2 = 127 см3

Высота: H2 = 35мм

Сторона вырезанного квадрата:

a2 = 2,36 см (реально 2 см)

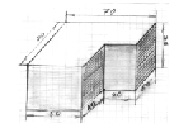
Рис. 8. Геометрический вид вставки

Верхняя вставка:Vвст3 = 32см3

Высота: H3 = 30мм

Сторона прямоугольника:

a3 = 5,87 см (реально 5,0 см)

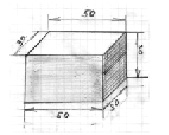
Рис. 9. Геометрический вид вставки

Задача № 2 Черный ящик в цилиндре «Кrass»

Дано:

Цилиндр с вставками. Вставки шары.

Вопросы: Сколько вставок? Каковы размеры и объёмы этих вставок? Представить рисунок вставки. Оценить точность измерений.

Рис. 10

Примечание: График программой Excel сильно сглажен, анализировать его сложно, для анализа воспользуемся графиками на миллиметровой бумаге.

Приложение № 2: График зависимости подъёма жидкости по капилляре от объёма вливаемой воды в сосуд «Krass» (Опыт повторила трижды. Анализирую красный график процесса, остальные рассуждения и таблицы аналогичны). На нижнем графике ?V – объём вливаемой воды одинаковый, высота воды в капилляре от объёма зависит линейно.

Анализ красного графика

1. Вид верхнего графика, зависимости высоты воды в капилляре, меняется от формы тела. Вижу периодичность – цикличность (похожа на синусоиду) процесса изменения высоты воды в капилляре. Изломов в графике не наблюдается. Это говорит о том, что там действительно шары, а не прямоугольные параллелепипеды. Таким образом, в данном сосуде четыре шара касаются друг друга.

2. Так как это сообщающиеся сосуды то высота max и min верхней функции есть радиус и диаметр шара:

D1 = 43мм – 1мм = 42мм

D2 = 84мм – 43мм = 41мм

D3 = 127мм – 84мм = 43мм

D4 = 167мм – 127мм = 40мм

Таким образом, шары примерно равных диаметров.

3. Рассчитаю погрешности прямых измеряемых величин:

Таблица 4

Рабочая таблица № 2

Таблица 5

Погрешности прямых измеряемых величин

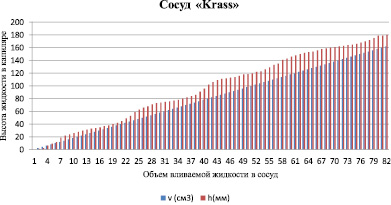
Рис. 11. Рабочий график

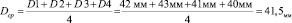
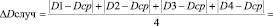
Dабсол = Dслуч + Dприбора = 1,0мм + 1,0мм = 2,0мм

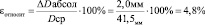
4. Первый способ расчета объема шара – физический:

Капилляра и цилиндр – сообщающиеся сосуды поэтому уровень воды в них одинаков.

Из графика видно, что общая высота вставленных шаров равна: H = 16,7 см

Найду длину внешней окружности при помощи ленты миллиметровки:

С = 15,4 см

С = d

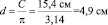
Внутренний диаметр окружности цилиндра равняется:

dвнутр = 4.9 см – 0,1 см = 4,8 см

Rвнутр = 2,4 см

Найду площадь внутренней окружности цилиндра:

Sвнут = R2

Sвнут = 3,14*5,76 см2 = 18 см2

Найду внутренней объём цилиндра:

Vвнутр = H* Sвнут

Vвнутр = 16,7 *18 см3=300,6 см3

Vшаров = Vвнутр – Vводы

Vшаров = 300,6 см3 – 158см3 = 142,6 см3

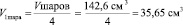
5. Второй способ расчета объема шара математический:

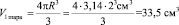
Выводы из решения задачи:

Параметры вставок: диаметр Dср = 41,5мм каждого из 4 шаров V1шара средн = 36,33 см3 это соответствует действительности (определила объём шара при помощи мензурки).

Задача № 3 Черный ящик в игрушке «Конус»

Дано:

Игрушка «Конус»:

1. В начале эксперимента установка пустая.

2 Во второй части эксперимента в установку вставлены куб и шар.

Вопросы: Каковы размеры и объёмы этих вставок?

Примечание: График программой Excel сильно сглажен, анализировать его сложно, для анализа воспользуемся графиками на миллиметровой бумаге.

Рис. 12

Приложение № 3: График зависимости подъёма жидкости по капилляре от объёма вливаемой воды в сосуд игрушки «Конус» (Опыт повторила трижды. Анализирую красный график процесса, остальные рассуждения и таблицы аналогичны). На нижнем черном графике ?V – объём вливаемой воды одинаковый, высота воды в капилляре от объёма зависит по параболе.

Анализ красного графика

1. Построены два графика зависимости высоты воды в капилляре от объема вливаемой жидкости в сосуд.

Черный график – эталон, построена зависимость, когда сосуд пустой.

Красный график – построена зависимость, когда в сосуде имеются вставки.

От 0 до 6 см3 точки совпадают – значит там вставок нет.

В зоне «А» графики параллельны – значит там вставок нет.

Вставки находятся от точки а до точки в и до точки с – так как вижу изломы на графике.

2. Отрезок (ав) в графике описывает шар – так как похож на параболу. Отрезок (вс) описывает куб – так как резкий подъём.

3. Расчеты параметров шара и куба: капилляра и конус – сообщающиеся сосуды поэтому уровень воды в них одинаков.

Dшара = 4,3см – 0,3см = 4см

Hкуба = 7,4см – 44,3см = 3,1см

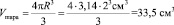
Vкуба = a3 = 29,8 см³

Выводы к главе: Анализируя графики, построенные при исследовательской деятельности, можно определить размеры вставок и их количество. Вид графиков усложняются если меняется форма сосуда от простой к сложной.

Заключение

Практическая значимость выполненной работы

Считаю, что с поставленной целью работы справилась успешно. Определила геометрические размеры и формы физических тел находящегося в «черном ящике», оценила точность измерения физических величин. Данную исследовательскую работу можно провести в домашних условиях без специального лабораторного оборудования.

При помощи данного метода я научилась определять форму и параметры тел скрытых от наших глаз. Эта методика позволяет определить геометрические размеры физических тел, когда тела нельзя наблюдать визуально. Эти тела могут находиться в трубах водопроводов, в нефтепроводах, в скважинах буровых установок. Этот метод полезно знать полиции и таможенникам, когда от их глаз прячут контрабанду в бензобаки, шины колёс, при условии, что нельзя воспользоваться рентгеном.

Физика, как наука, даёт теоретические знания и формирует практические навыки исследовательской деятельности. На протяжении всей работы имела возможность провести несколько опытов и понять много интересных фактов из раздела физики и математики.

Таблица 6

Рабочая таблица № 3

Рис. 13. Рабочий график

Работа меня заинтересовала настолько, что я бы хотела продолжить изучение экспериментальной части физики в дальнейшем, и продолжать экспериментировать дома при подготовке к олимпиадам по физике и к итоговой аттестации.

«Опыт же не только учит: он увлекает, заставляет лучше понимать то явление, которое он демонстрирует. Ведь известно, что человек, заинтересованный в конечном результате, обязательно добивается успеха. Чем более простыми средствами будет ставиться эксперимент, тем он ценнее». П.Л. Капица, академик [4].

Библиографическая ссылка