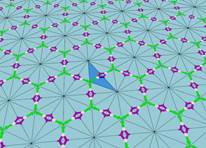
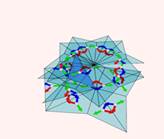
Все знакомы с замечательной игрушкой – калейдоскоп. Переливающиеся узоры завораживают, можно часами сидеть и рассматривать их, ведь бесконечный мир зазеркалья очень интересный и загадочный. Но разобрав игрушку … не ясно, не понятно, как этот манящий мир зазеркалья образуется, от чего зависит правильное изображение в калейдоскопе…ведь мы же находимся не в сказке.
Актуальность исследования: Мир зазеркалья калейдоскопа загадочен тем, что его изображение должно быть “правильным”, но к сожаленью не все знают от чего и как это изображение образуется.
Цель проекта: Выяснить, зависит или нет правильное изображение в калейдоскопе от прямой призмы, которая находится внутри него.
Задачи исследования:
1. Найти и изучить теоретический материал по теме «Зеркальная и поворотная симметрия»;
2. Выяснить, какой принцип заложен в работе калейдоскопа;
3. Исследовать зависимость количества изображений от величины угла между зеркалами;
4. Ознакомиться с устройством калейдоскопа;
5. Собрать информацию о калейдоскопах и различных прямых призмах в них;
Выяснить при каких прямых призмах получается правильное изображение;
Cравнить недостатки и преимущества прямых призм в использовании в калейдоскопе;
6.Изготовить свой калейдоскоп;
7.Обобщить полученную в результате исследования информацию.
Гипотеза: “Правильное изображение” в калейдоскопе зависит, о того какая прямая призма находится внутри него.
Хоть нам и кажется калейдоскоп волшебством, но это не так, потому что в основе бесконечного загадочного мира калейдоскопа лежат законы математики, геометрии и физики: зеркальная и поворотная симметрия; принцип отражения света от плоского зеркала и т.д.
Калейдоскоп (слово произошло от трех греческих слов - красивый, вид, смотрю). Считается, что калейдоскоп изобрел шотландский физик Дэвид Брюстер. В 1816 году он запатентовал свой калейдоскоп.
1. Симметрия (от греческого “symmetria”) - означает одинаковость в расположении частей.
В калейдоскопе совмещаются два вида симметрии: зеркальная и поворотная. Расположив зеркала под определенным углом, можно увидеть отражение, отражение отражения и т.д.
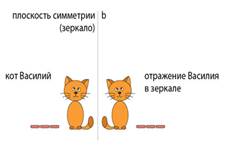
Отражение – это наиболее известная и чаще других встречающаяся в природе разновидность симметрии. Зеркало в точности воспроизводит то, что оно “видит”, но обращает пространственный порядок: например, правая рука Вашего двойника окажется левой т.к. пальцы будут расположены на ней в обратном порядке.
Зеркальная симметрия – это такая симметрия, когда одна фигура зеркально отражает (повторяет) другую т.е.каждая половинка служит зеркальным отражением другой, а разделяющая их плоскость называется плоскостью зеркального отражения (плоскостью симметрии).
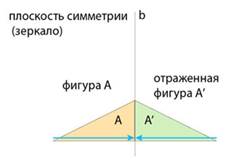
На рисунке оранжевый треугольник (фигура А) отражается в зеркале, в результате, получаем фигуру А' - точную копию фигуры А, но, все что было слева, стало на таком же расстоянии от плоскости симметрии (прямая b) справа.
Это самый распространенный вид симметрии — мы видим его повсюду в природе, а также в искусстве, технике и даже в музыке, лингвистике и других науках.
Провел эксперимент, в хоте которого выяснил свойства предметов при зеркальной симметрии: изображение любого предмета в плоском зеркале равно по размерам самому предмету и расположено относительно зеркала симметрично предмету.
Поворотная симметрия – при ней внешний вид узора не изменяется, если его повернуть на некоторый угол вокруг оси. Примером может служить детская игра “вертушка” с поворотной симметрией. Во многих танцах фигуры основаны на вращательных движениях, нередко совершаемых только в одну сторону (т.е. без отражения), например, хороводы. Комбинируя отражение с поворотом, мы получим то, что видно в калейдоскопе.
Все две симметрии необходимы для правильного изображения.
2. Калейдоскоп – это оптический прибор, в основе действия которого лежит принцип отражения света от плоских зеркал, образующих между собой угол.
Именно зеркало обладает гладкой поверхностью, поэтому отражает свет под четким углом. Свет при этом отражается, подчиняясь закону отражения - именно этот принцип и лежит в основе работы калейдоскопа.
Именно зеркала, которые используются в калейдоскопе, и дают мнимое расположенное симметрично относительно зеркала, изображение.
Получается, что именно благодаря зеркальной симметрии и принципу отражения света от плоского зеркала мы видим симметричное изображение в калейдоскопе.
3.Внутри калейдоскоп может стоять от 2-3-х зеркал до 4-х или более. Чтобы понять принцип работы калейдоскопа проведу опыт с зеркалами. Возьмём зеркало и положу перед ним фишку. Видим две фишки: одну в оригинале и одну в отражении "за зеркалом". В зеркале мы видим изображение фишки, находящееся на расстоянии равном расстоянию до зеркала. Возьму теперь два зеркала расположенных под углом 1200 друг к другу и повторим наш эксперимент. Мы видим три фишки: одну в оригинале и две в отражении. Зеркальный угол с раствором 90° покажет то же изображение четыре раза. А два зеркала, угол между которыми составляет 72°, дадут нам пятикратное изображение. Если угол между зеркалами 600, то изображений 6, 30 градусов —12 и т.д. Когда угол становиться меньше, количество предметов увеличивается. т.е.- количество изображений в зеркалах зависит от величины углов между зеркалами. Число изображений равно результату деления 360° на величину угла между зеркалами, то есть 1800, 1200, 900, 720, 600, 45°, 360, 300 и т. д. В зависимости от числа, на которое производится деление, мы видим фишку 2, 3, 4, 5, 6, 8, 10 и 12 раз. Фишка совершает в зеркале "полный оборот". Таким образом, образует симметричный узор.
Количество изображений и красота рисунка в калейдоскопе как раз и зависит от количества зеркал, которые находиться в призме.
|
|
|
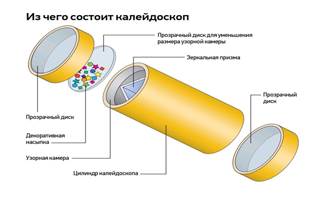
4. Калейдоскоп внутри снабжен зеркалами, поставленными под определенными углами по отношению к друг другу (прямая призма).
В одном из оснований призмы — двойное стеклянное дно, между стёклами насыпаны мелкие разноцветные предметы. В противоположном основании призмы — окуляр. При фиксированном положении калейдоскопа из предметов складывается картинка в «основной» фигуре. Она многократно отражается в стенках ? зеркалах, и наблюдатель через окуляр видит симметрично ? правильный разноцветный узор. При повороте калейдоскопа предметы пересыпаются, возникает новый, но тоже правильный узор. Также, красота узора -зависит еще как раз от этих предметов.
5. Рассмотрим несколько треугольных призм.
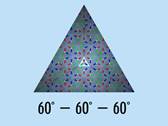
Прямую треугольную призму, в основании которой лежит равносторонний треугольник, с углами 600-600-600
|
|
|
|
|
|
(а) |
(б) |
|
(в) |
(г) |
|
|
|
|
|
|
(д) Степени отражения (зеркальная и поворотная симметрия) |
||
|
|
|
|
|
Правильное изображение |
(е)Устойчивость |
|
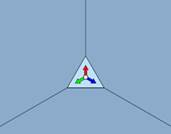
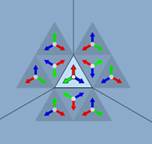
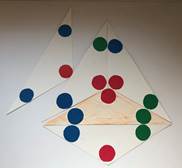
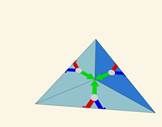
Картинка, образующаяся в фундаментальном треугольнике (а). Заменим её на более простую, математически связанную с самим фундаментальным треугольником — три разноцветные стрелки (б) одинаковой длины, отложенные от центра треугольника перпендикулярно зеркалам.
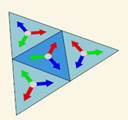
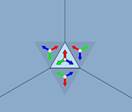
Если бы у нас было одно зеркало, то на этом всё бы и закончилось (в); общая картинка состояла бы из фундаментального треугольника и его образа в зеркале. Но в случае калейдоскопа все три стороны фундаментального треугольника зеркальные, и, значит, наблюдатель заведомо увидит сам фундаментальный треугольник и три его симметричные относительно сторон копии (г). На самом же деле, как известно из практики, картинка будет гораздо больше. Дело в том, что отражения зеркала в зеркале снова «работают» как зеркало. То есть природа продолжает симметрично отражать копии треугольников относительно их «виртуальных» сторон (д). Получающаяся картина должна заполнять всю плоскость (е), различные копии-отражения фундаментального треугольника не должны накладываться друг на друга, создавая мешанину, не должны обрезаться. Ну а главная характеристика «правильного» калейдоскопа — изображение, получившееся после отражения в зеркалах, наблюдатель должен видеть как реальный объект: если смещаться относительно зеркал, то изображение не должно изменяться (устойчивость (з)). И оно действительно устойчиво: если покачать калейдоскоп, то изображение меняться не будет. Даже в тех местах, где ребро между зеркалами калейдоскопа перемещается относительно рисунка, он остается постоянным вне зависимости от положения калейдоскопа и его рёбер.
Важно, что видимая картина «устойчива», не изменяется при небольших шевелениях калейдоскопа. Если узор «устойчивый» и симметричный на всем бесконечном мире зазеркалья— то только лишь в этом случае изображение будет правильным и только в этом случае устройство и будет являться калейдоскопом.
Если рассмотреть прямую треугольная призма в основании которой лежит прямоугольный равнобедренный треугольник, с углами 900-450-450
и прямую треугольную призму в основании которой лежит прямоугольный треугольник, с углами 900-300-600 – то у калейдоскопов, построенных на фундаментальных треугольниках с перечисленными наборами углами- все описанные свойства также выполняются.
А бывают ли еще какие-то случаи?
Чтобы ответить на этот вопрос проведу эксперимент.
Рассмотрим прямую треугольную призму в основании которой лежит произвольный треугольник любыми другими с углами.
|
|
|
|
|
|
Фундаментальный треугольник с произвольными углами |
Отображения первого порядка |
||
|
|
|
|
|
|
|
|
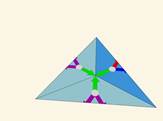
Видим, что симметрия отображения уже в первом порядке нарушается … |
|
Т.е. видим, что не любая прямая треугольная призма создает правильное изображение в калейдоскопе. Разберем это:
|
|
|
В случае же произвольного треугольника в отражениях первого порядка — относительно сторон самого фундаментального треугольника — присутствует нестыковка. Образы, полученные отражениями относительно сторон, не симметричны друг другу.
|
|
|
В случае же произвольного треугольника, если начать делать дальше всевозможные его отражения на плоскости, они будут накладываться друг на друга, изображение будет складываться из как-то перемешанных обломков изначального изображения и не будет регулярным и ни о каком красивом правильном изображении говорить не приходится.
Т.к. Изображение формируется в каждом из зеркал раздельно по уже указанному принципу «образ зеркала в зеркале, снова работает как зеркало». Но изображение, формирующееся в одном из зеркал, не переотражается в другом зеркале.
|
|
|
Сюрпризы, преподносимые треугольником с произвольными углами на этом, не заканчиваются-возникает неустойчивость
и изменчивость изображения.
При повороте калейдоскопа предметы пересыпаются, возникает новый, но тоже симметричный узор. Чтобы обеспечить симметрию узора, его устойчивость и его «правильное» изображение — лишь в этом случае устройство называют калейдоскопом, — для построения прямой призмы подходят только три вида треугольников:
1.Треугольная призма в основании которой лежит равносторонний треугольник, с углами 600-600-600.
2.Треугольная призма в основании которой лежит прямоугольный равнобедренный треугольник, с углами 900-450-450
3.Треугольная призма в основании которой лежит прямоугольный треугольник, с углами 900-300-600.
Но самым распространённом типом калейдоскопов- треугольная призма в основании которой лежит равносторонний треугольник, с углами 600-600-600 Этот вариант удобен и с производственной точки зрения — все зеркала одинаковые.
Если в основании зеркальной прямой призмы использовать не треугольник, а произвольный многоугольник, то “правильное” изображение в калейдоскопе получиться лишь при использовании четырех зеркал, поставленных по сторонам прямоугольника т.е.при использовании прямой четырехугольной призмы.
|
|
|
|
К сожалению наш глаз, глядя в глазок калейдоскопа, видит не весь бесконечный мир зазеркалья, который образуется в калейдоскопе –и поэтому многие считают, что можно использовать любую прямую призму в калейдоскопе. НО ни какие другие прямые призмы для создания калейдоскопа не подходят, т.к. они не создадут правильное изображение в калейдоскопе. Для доказательства, я провел эксперимент:

Правильным изображение можно назвать лишь когда оно симметричное, без наложений и устойчивое во всех бесконечных отображениях калейдоскопа.
т.о. Гипотеза: Правильное изображение в калейдоскопе зависит, о того какая прямая призма находиться внутри него- нашла свое подтверждение
В заключении своего исследования я изготовил собственный калейдоскоп.
Выводы:
Узор, порождаемый зеркалами калейдоскопа, под правильным выбранным углом, обладает и зеркальной и поворотной симметрией.
Основный принцип, который заложен в основе калейдоскопа это: принцип отражения света от плоского зеркала, благодаря которому, расположив зеркала под определенным углом, мы видим симметричные отражение, отражение отражения и т.д.
Количество изображений и красота рисунка в калейдоскопе зависит от количества зеркал, которые находиться в призме и от декоративной насыпки, которую используют в калейдоскопе.
Изображение в калейдоскопе считают правильным, когда оно симметричное, без наложений и устойчивое во всех бесконечных отображениях калейдоскопа.
Правильное изображение в калейдоскопе можно добиться, только при использовании 4 видов прямых призм в ее устройстве:
а. Треугольная призма в основании которой лежит равносторонний треугольник, с углами 600-600-600.
б. Треугольная призма в основании которой лежит прямоугольный равнобедренный треугольник, с углами 900-450-450
в. Треугольная призма в основании которой лежит прямоугольный треугольник, с углами 900-300-600.
г. Четырехугольные призмы.
Изготовил собственный калейдоскоп с прямой треугольной призмой в основании которой лежит равносторонний треугольник, с углами 600-600-600.
Библиографическая ссылка
Зайцев А.А. КАЛЕЙДОСКОП // Старт в науке. 2020. № 1. ;URL: https://science-start.ru/ru/article/view?id=1822 (дата обращения: 13.03.2026).