«Весь смысл жизни заключается в бесконечном завоевании неизвестного; в вечном усилии познать больше».
Эмиль Золя
Однажды в одном из выпусков проекта «Открытие Китая» с Евгением Колесовым на Первом канале я увидел сюжет об удивительном изобретении китайского пенсионера – велосипеде с «угловатыми» колесами. Переднее колесо представляет собой пятиугольник, заднее – треугольник. Меня заинтересовало не только само по себе данное изобретение, но и необычная геометрическая фигура – круглый треугольник. Я узнал, что он называется треугольником Рёло и обладает интересными свойствами. Свою исследовательскую работу я решил посвятить изучению свойств и областей применения треугольника Рёло.
Цель моей исследовательской работы:
1. Изучение основных свойств треугольника Рёло и его областей применения.
2. В соответствии с поставленной целью в работе решаются следующие задачи:
3. Познакомиться с историей изобретения треугольника Рёло;
4. Рассмотреть способы построения круглого треугольника;
5. Рассмотреть и изучить свойства треугольника Рёло;
6. Выяснить области практического применения треугольника Рёло;
7. Создать модель круглого колеса.
Актуальность. Исторически геометрия начиналась с треугольника, поэтому треугольник – символ геометрии. Геометрия треугольника дает возможность почувствовать красоту математики. Каждый любитель геометрии треугольника имеет возможность открыть нечто новое и пополнить её сокровищницу собственной драгоценной находкой, ибо геометрия поистине неисчерпаема. В современном мире при быстро развивающихся технологиях нельзя обойти фигуру постоянной ширины – треугольника Рёло.
Объект исследования: треугольник Рёло.
Методы исследования: изучение научной литературы по теме, сбор и систематизация материалов, анализ и интерпретация полученных данных.
Гипотеза. Используя свойства треугольника Рёло, можно сделать его модель своими руками, показать практическое применение круглого треугольника.
Теоретическая часть
Определившись с темой и целью моего исследования, я занялся планированием, сформулировал задачи, определился с источниками информации, распределил время. Затем я начал сбор информации. Информацию для своей работы я собирал из разных источников: энциклопедии, интернет, собственные наблюдения.
Что такое «круглый» треугольник?
Треугольник Рёло или «круглый треугольник» – плоская выпуклая геометрическая фигура, представляющая собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло (рис. 1) [1].
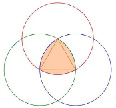
Рис. 1
Треугольник Рёло является простейшей после круга фигурой постоянной ширины. [2] Если к треугольнику Рёло провести пару параллельных опорных прямых, то независимо от выбранного направления расстояние между ними будет постоянным. Это расстояние называется шириной. Поскольку одна из прямых всегда проходит через вершину треугольника, а другая касается противоположной дуги, то ширина треугольника равна радиусу образующих его кругов (рис. 2) [2].
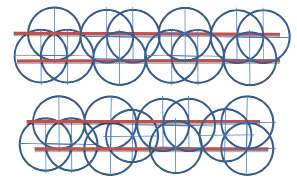
Рис. 2
Способы построения треугольника Рёло
I способ. Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выбирается произвольно, центром второй может быть любая точка первой окружности, а центром третьей – любая из двух точек пересечения первых двух окружностей (рис. 3) [2].
1. Окружность (A; R)
2. Окружность (В; R), где точка В ∈ окружности (А; R)
3. Окружность (С; R), где точка С – точка пересечения окружностей (A; R) и (В; R)
4. Негладкая замкнутая кривая АВС – треугольник Рёло.
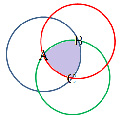
Рис. 3
II способ: Треугольник Рёло можно построить с помощью правильного треугольника. На каждой стороне треугольника построим дугу окружности, радиусом, равным длине стороны. Треугольник Рёло представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло [2].
1. Правильный треугольник АВС (АВ = ВС = СА)
2. Окружность (A; R=АВ)
3. Окружность (В; R)
4. Окружность (С; R)
5. Область пересечения трех кругов, а так же негладкая замкнутая кривая АВС – треугольник Рёло (рис. 4).
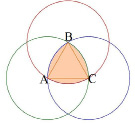
Рис. 4
Свойства треугольника Рёло
Треугольник Рёло обладает осевой симметрией. Он имеет три оси симметрии, каждая из которых проходит через вершину треугольника и середину противоположной дуги (рис. 5) [4].
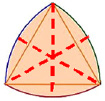
Рис. 5
Треугольник Рёло является простейшей после круга фигурой постоянной ширины. [4] То есть если к треугольнику Рёло провести пару параллельных опорных прямых, то независимо от выбранного направления расстояние между ними будет постоянным. Это расстояние называется шириной треугольника Рёло. Треугольник Рёло постоянно касается обеих прямых. Действительно, одна точка касания всегда расположена в одном из «углов» треугольника Рёло, а другая – на противоположной дуге окружности. Значит, ширина всегда равна радиусу окружностей, т.е. длине стороны изначального правильного треугольника (рис. 6).
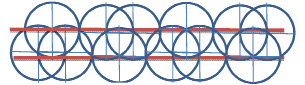
Рис. 6
С каждой из своих опорных (параллельных) прямых треугольник Рёло имеет лишь по одной общей точке (рис. 7) [4].
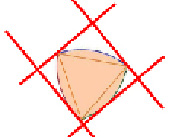
Рис. 7
Теорема Барбье: [5] Все кривые постоянной ширины d имеют одинаковую длину, равную πd, где d – ширина.
Расстояние между двумя любыми точками треугольника Рёло не может превышать его ширины [4] (рис. 8).
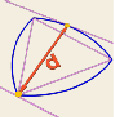
Рис. 8
Отрезок, соединяющий точки касания двух параллельных опорных прямых к треугольнику Рёло, перпендикулярен к этим опорным прямым [4] (рис. 9).
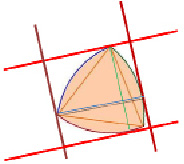
Рис. 9
Через любую точку границы треугольника Рёло проходит по крайней мере одна опорная прямая [4].
Треугольник Рёло, как и любую другую фигуру постоянной ширины, можно вписать в квадрат, в котором треугольник Рёло будет вращаться, постоянно касаясь всех четырёх сторон (рис. 10) [4, 11].
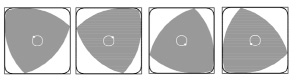
Рис. 10
Исторические сведения
Название фигуры происходит от фамилии немецкого механика Франца Рёло (1829 – 1905).
Франц Рёло не является первооткрывателем «круглого треугольника», хотя он и подробно исследовал эту фигуру [10].

Франц Рёло
Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг окружности Леонард Эйлер в XVIII веке [10].
Тем не менее, подобная фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Треугольник Рело есть в его манускриптах A и B, хранящихся в Институте Франции, а также в Мадридском кодексе [10].
Примерно в 1514 году Леонардо да Винчи создал одну из первых в своём роде карт мира. Поверхность земного шара на ней была разделена экватором и двумя меридианами на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло, собранными по четыре вокруг полюсов (рис. 11) [3].

Леонард Эйлер
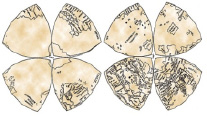
Рис. 11
Практическое применение треугольник Рёло
Сверло Уаттса
В 1914 году английский инженер Гарри Джеймс Уаттс изобрёл инструмент для сверления квадратных отверстий.
Сверло Уаттса представляет собой треугольник Рёло, в котором прорезаны углубления для отвода стружки и заточены режущие кромки [6, 11].
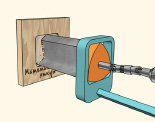
Рис. 12
Двигатель Ванкеля
Треугольник Рёло используется и в автомобильных двигателях. Сконструировал этот роторно-поршневой двигатель в 1957 году немецкий инженер Ф. Ванкель, немецкий инженер и изобретатель (1902–1988). Внутри примерно цилиндрической камеры по сложной траектории движется трёхгранный ротор-поршень – треугольник Рёло. Он вращается так, что три его вершины находятся в постоянном контакте с внутренней стенкой корпуса, образуя три замкнутых объёма, или камеры сгорания. Фактически каждая из трёх боковых поверхностей ротора действует как поршень. При вращении ротора внутри корпуса объём трёх боковых создаваемых им рабочих камер постоянно изменяется, действуя как насос. Ротор-поршень установлен свободно на эксцентрике вала и соединён с зубчатым колесом с внутренними зубьями, обкатывающимися вокруг неподвижной шестерни с наружными зубьями, ось которой совпадает с осью эксцентрикового вала. Двигатель Ванкеля имеет множество преимуществ перед обычным ДВС: РПД значительно компактней и легче, поэтому, при установке его на автомашину, центр тяжести оказывается значительно ниже, а устойчивость автомобиля – выше. Впервые на серийных автомобилях этот двигатель стала устанавливать компания Mazda. Он установлен на моделях MazdaRX-7 и MazdaRX-8 [7].
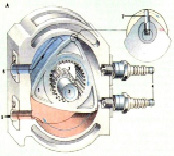
Рис. 13
Грейферный механизм в кинопроекторах
Грейферный механизм – это ещё одно применение треугольника Рёло в механике. Он осуществляющий покадровое перемещение плёнки в кинопроекторах. Двигатели дают равномерное вращение оси, а чтобы на экране было чёткое изображение, плёнку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть, и так 18 раз в секунду. Именно эту задачу решает грейферный механизм. Он основан на треугольнике Рёло, вписанном в квадрат, и двойном параллелограмме, который не даёт квадрату наклоняться в стороны. Действительно, так как длины противоположных сторон равны, то среднее звено при всех движениях остаётся параллельным основанию, а сторона квадрата – всегда параллельной среднему звену. Чем ближе ось крепления к вершине треугольника Рёло, тем более близкую к квадрату фигуру описывает зубчик грейфера [8, 11] (рис. 14).
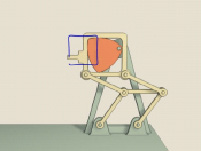
Рис. 14
Рассмотрим в качестве примера грейфер проектора «Луч-2», основанный на треугольнике Рёло, который вписан в рамку-квадрат и закреплён на двойном параллелограмме. Вращаясь вокруг вала привода, треугольник двигает рамку с расположенным на ней зубом (рис. 15). Зуб входит в перфорацию киноплёнки, протаскивает её на один кадр вниз и выходит обратно, поднимаясь затем к началу цикла (рис. 16) [8].
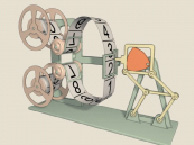
Рис. 15
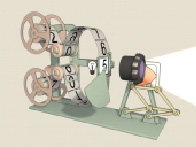
Рис. 16
Его траектория тем ближе к квадрату, чем ближе к вершине треугольника закреплён вал (идеально квадратная траектория позволила бы проецировать кадр в течение ¾ цикла)
Кулачковые механизмы
Треугольник Рёло применяется в кулачковых механизмах. Так в начале XIX века он использовался в кулачковых механизмах некоторых паровых двигателей. В этих механизмах вращательное движение кривошипа поворачивает треугольник Рёло, прикреплённый к толкателю передаточными рычагами, что заставляет толкатель совершать возвратно-поступательное движение. По терминологии Рёло, это соединение образует «высшую» кинематическую пару, поскольку контакт звеньев происходит по линии, а не по поверхности. В подобных кулачковых механизмах толкатель при достижении крайнего правого или левого положения остаётся некоторое конечное время неподвижен.
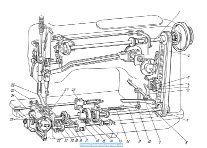
Рис. 17
Треугольник Рёло используется в механизмах швейных машин зигзагообразной строчки (рис. 17) [11].
В качестве кулачка треугольник Рёло использовали немецкие часовые мастера в механизме наручных часов A. Lange & Söhne «Lange 31» (рис. 18) [9].

Рис. 18
Плектр
Треугольник Рёло – распространенная форма плектра (медиатора): тонкой пластинки, предназначенной для игры на струнах щипковых музыкальных инструментов [3].


Рис. 19
Крышки для люков
В форме треугольника Рёло можно изготавливать крышки для люков – благодаря постоянной ширине они не могут провалиться в люк. В Сан-Франциско, для системы рекупе-рирования воды корпуса люков имеют форму треугольника Рёло, но их крышки имеют форму равносторонних треугольников [3].

Рис. 20
Сувенирные монеты
Форму треугольника Рёло имеют сувенирные монеты Бермуд (рис. 21) и памятная монета Канады (рис. 22) [3].

Рис. 21

Рис.22
Применение круглого треугольника в архитектуре
Форма треугольника Рёло используется и в архитектурных целях. Конструкция из двух его дуг образует характерную для готического стиля стрельчатую арку, однако целиком он встречается в готических сооружениях довольно редко. Окна в форме треугольника Рёло можно обнаружить в церкви Богоматери в Брюгге, а также в шотландской церкви в Аделаиде [3].



Церковь Богоматери в Брюгге


Собор Святого Сальватора в Брюгге


Церковь Святого Михаила (Люксембург)
Треугольник Рело используют и в архитектуре, которая не относится к готическому стилю. Например, построенная в 2006 году в Кельне 103–метровая башня под названием «Кельнский треугольник». В сечении имеет именно форма этой фигуры [3].
В 2006 году для широкой публики был открыт музей компании Mercedes-Benz в Штутгарте. Здание основано на уникальной концепции в форме треугольника Рёло [3].

Башня делового центра «Кёльнский треугольник» в Кёльне

Музей компании Mercedes-Benz в Штутгарте
Треугольник Рёло в фантастической литературе
В научной фантастике авторы также используют удивительные свойства треугольника Рёло. Так в рассказе Пола Андерсона «Треугольное колесо» [12] экипаж землян совершил аварийную посадку на планете, население которой не использовало круглые колеса, так как всё круглое находилось под религиозным запретом. В сотнях километров от места посадки предыдущая земная экспедиция оставила склад с запасными частями, но перенести оттуда необходимый для корабля двухтонный атомный генератор без каких-либо механизмов было невозможно. В итоге землянам удалось соблюсти табу и перевезти генератор, используя катки с сечением в виде треугольника Рёло.
Кривые постоянной ширины
Оказывается, фигурами постоянной ширины являются не только круг и треугольник Рёло. Фигуры постоянной ширины можно получить из правильных многоугольников с нечетным числом сторон. Эти фигуры называют правильными многоугольниками Рёло (рис.23). Геометрическое их построение несложно: в правильных многоугольниках с нечетным числом сторон надо провести дуги с центрами в вершинах и радиусами, равными по длине диагонали, которая ведет к вершинам, ограничивающим противоположное ребро (Приложение 1) [3].
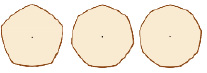
Рис. 23
Практическое применение знаний о треугольнике Рёло
Изучив свойства треугольника Рёло [3], я решил изготовить круглый каток и каток с сечением в виде круглого треугольника. Цель изготовления таких катков – выяснить, а можно ли применять круглый треугольник для перемещения груза. Для этого груз нужно расположить на плоской подставке, установленной на катках, а затем толкать его. При этом перемещении важно, чтобы груз не двигался вверх и вниз, так как тряска потребует дополнительных усилий от толкающего. Для того чтобы движение по каткам было прямолинейным, их сечение должно представлять собой фигуру постоянной ширины. (Приложение 2). Я убедился, что сечение в виде треугольника Рёло будет ничуть не хуже и позволит передвигать предметы столь же прямолинейно, как круглые катки. Несмотря на то, что катки в форме треугольника Рёло позволяют плавно перемещать предметы, такая форма не подходит для изготовления колёс, поскольку треугольник Рёло не имеет фиксированной оси вращения.
Заключение
Колесо, изобретенное несколько тысяч лет назад, произвело переворот в жизни человека. Постоянство ширины явилось для колеса определяющим свойством, следствием которого явилось техническое завоевание мира. Я рассмотрел это свойство в треугольнике Рёло. Проведя практические эксперименты, я убедился в том, что средство передвижения с колесами в форме треугольника Рёло создать реально. Собственно кататься на этих треугольниках можно только в том случае, если только перекатываться на них, а не использовать в качестве колес с осью.
Проводя свои исследования, я убедился, что открытие треугольника Рёло сделало переворот в научно-техническом мире, так как отличительные его свойства находят множество применений.
Работая над темой, я понял, что, несмотря на то, что треугольник называют простейшей фигурой, он скрывает в себе еще много тайн, которые только предстоит разгадать ученым.
Приложение 1
Правильные многоугольники Рёло




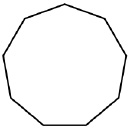
Приложение 2
Изготовление круглого катка и катка с сечением в виде круглого треугольника







Приложение 2
Изготовление круглого катка и катка с сечением в виде круглого треугольника



Библиографическая ссылка
Першин И.С. ТРЕУГОЛЬНИК РЁЛО // Старт в науке. 2019. № 5-1. ;URL: https://science-start.ru/ru/article/view?id=1711 (дата обращения: 28.02.2026).
