• Авторы
• Научный руководитель
• Файлы
• Литература

Ясаков И.И. 1

---

1 г. Кандалакша, МАОУ «Основная общеобразовательная школа №19», 6 «В» класс

Меркулова Т.Н. (г. Кандалакша, МАОУ «Основная общеобразовательная школа №19»)

Статья в формате PDF

0 KB

1. Якир А.Г. Математика 6 / А.Г. Якир. – М.: Вентана-Граф, 2014. – 104 с.

2. https://www.adme.ru/svoboda-kultura/9–nelepyh-sluchajnostej-kotorye-izmenili-hod-istorii-1466015/ © AdMe.ru. – режим доступа свободный.

3. Тиммеш, К Придумано девочками / К. Тиммеш. – М.: Лабиринт, 2016. – C. 25.

4. Универсальная научно-популярная онлайн-энциклопедия [электронный ресурс]. – http://www.krugosvet.ru/. – Режим доступа свободный.

5. https://habrahabr.ru/post/274975/. – режим доступа свободный.

6. http://datareview.info/article/znakomstvo-s-metodom-monte-karlo/. – режим доступа свободный.

7. Гены и наследственность // Хочу всё знать про всё на свете: Справочник для детей / Ридерс Дайджест, 2001. – C. 132.

8. http://hochuvidet.ru/kak-opredelit-tsvet-glaz-budushhego-rebenka/. – режим доступа свободный.

9. http://www.aif.ru/dontknows/about/1093487. – режим доступа свободный.

10. https://www.woolwares.ru/news/pyat-znachimykh-v-istorii-sluchajnoste/. – режим доступа свободный.

11. [http://itmydream.com/citati/book/dzhodzho-moies-odin-plyus-odin. – режим доступа свободный.

Мы живём в мире, где каждый день происходят случайные события. Многие из них остаются незамеченными, а некоторые меняют ход истории. Например, случайно изменилась погода, ученик забыл дома тетрадь или Колумб случайно открыл Америку. Люди часто используют в речи выражения «возможно», «вероятно», «будем надеяться», но вычислением появления случайного события, изучением его закономерностей занимается «Теория вероятностей». На уроках математики в 6 классе мы познакомились с её основными понятиями «случайное событие» и «вероятность» [1]. Узнали, что события бывают достоверными, маловероятными и невероятными. Научились решать простейшие задачи.

У нас возник вопрос: зачем нужны эти знания, где их можно применить, кроме урока математики? Проведённый в классе опрос показал, что большинство учеников считают, что это понятие применяется только в математике и в азартных играх. (Приложение 1)

Гипотеза: понятие «вероятность» применяется не только в математике, но и других областях человеческой деятельности.

Цель: установить, в каких сферах человеческой деятельности применяется понятие «вероятность».

Задачи:

1. Изучить источники, познакомиться с историей «Теории вероятностей».

2. Систематизировать информацию о сферах применения вероятности.

3. Проверить опытным путём действие Закона больших чисел.

4. Поставить эксперимент с игральной костью. Сравнить частоту события с вероятностью.

5. Найти ответ на вопрос: можно ли выиграть в лотерее?

6. Повторить опыт Бюффона по определению числа ПИ с помощью иголок.

7. Поставить компьютерный эксперимент по определению площади нестандартной фигуры методом «Монте-Карло».

8. Провести опыт с семенами.

9. Сделать выводы.

Объект исследования: различные сферы человеческой деятельности.

Предмет исследования: вероятность.

Методы исследования: поиск и анализ информации, опрос, эксперимент, компьютерное моделирование, наблюдение и вычисление. Для проведения опытов мы использовали игральную кость и интерактивную модель кубика в приложении SMART, для создания компьютерной модели и вычисления площади фигуры – MS EXCEL, для повторения опыта Бюффона – швейные иголки.

Обзор источников и литературы

Из статьи «Десять случайностей, которые изменили мир»[2], опубликованной на сайте ADME мы узнали, как был открыт антибиотик пенициллин, благодаря которому человечество победило многие болезни. Оказывается, учёный Александр Флеминг очень не любил наводить порядок в лаборатории, однажды все его препараты покрылись плесенью, и он случайно догадался, что именно из неё может получиться лекарство. В книге «Придумано девочками» Тиммеш Кетрин рассказала, как девушки случайно стали изобретательницами: «они просто хотели справиться с трудностями, которые возникли в их жизни»[3]. Так появились дворники для ветрового стекла, жидкий корректор, чипсы, мороженое на палочке и многие другие, привычные для нас предметы.

«Теория вероятностей». Занимается вычислением появления случайного события, изучением его закономерностей. О ней мы узнали из универсальной научно-популярной онлайн-энциклопедии «Кругосвет» [4]. Это достаточно молодая область математики, её первые задачи были связаны с игральными костями и картами. В XIII веке Фурниваль подсчитал все возможные исходы при бросании трёх костей. Чуть позже, в XIV в. математики Дж. Кардано и Н. Тарталья, а в XVII в. Б. Паскаль, также изучали возможность выигрыша в азартных играх. П.Лаплас, который считается одним из создателей «Теории вероятностей», заметил, что: «она представляет собой не что иное, как здравый смысл, сведенный к вычислениям»[4]. Главный принцип науки – Закон больших чисел, по которому, проведя только очень большое количество испытаний, можно прогнозировать результат.

Опираясь на этот Закон, используя случайные величины, в 1777 году Бюффон предложил оригинальный способ для вычисления числа ПИ. Иглу длины L, см, бросали многократно на лист бумаги, расчерченный параллельными прямыми через каждые R, см, и подсчитывали количество пересечений. Из формулы

P=(2L)/(R?),

где P – отношение количества пересечений к числу бросаний получили, что ?=(2L)/(RР).

На сайтах «Хабрахабр» [5] и «Datareview» [6] мы нашли информацию о том, что в 1949 году, благодаря появлению первых ЭВМ, произошёл резкий скачок в развитии науки, так как стало возможным моделировать различные процессы с использованием случайных чисел и быстро вычислять результаты испытаний. Так, появился метод Монте-Карло. Этот метод применяли при моделировании взрыва атомной бомбы. А Джон фон Нейман предложил использовать его в мирных целях для решения широкого круга задач по физике, химии и метеорологии. В частности, для вычисления площадей фигур сложной формы. Например, озера или болота по фотографии.

В статье «Гены и наследственность», опубликованной в «Справочнике для детей» [7], мы прочитали, что вероятностные методы нашли своё применение в естественных науках. Так, генетики могут вычислить пол будущего ребёнка и цвет его глаз. Интересно, что большинство населения Земли имеют карие глаза, тысячу лет назад голубоглазых людей не было совсем, а самый редкий цвет глаз – зелёный [8].

И последнее, из электронной версии газеты «Аргументы и факты» [9] мы узнали, что в сельском хозяйстве перед посевной обязателен прогноз на новый урожай.

Экспериментальная часть

Эксперимент с игральной костью

Поскольку зарождение «Теории вероятностей» связано с игральной костью, то первый опыт мы поставили с этим предметом и использовали электронный кубик (приложение доски SMART). Участниками стали одноклассники. Каждому было предложено назвать число и бросить игральную кость. Вероятность выпадения любой цифры при однократном бросании равна 1/6. Вероятность угадать – 1/36. Проведено 73 испытания. Мы заметили, что чем больше количество испытаний, тем ближе среднее количество выпадений цифры и угадываний к вычисленной вероятности. Чаще других выпадала «6», реже «3» и «4». Парадокс – чаще угадывали «3» (Приложение 2).

Лотерея и азартные игры

Выиграть в лотерею – большая редкость, но некоторым везёт. Известны удивительные случаи. Мэри Волленс из Канады, приобрела два лотерейных билета, вписала цифры, которые ей приснились – и каждый билет выиграл по 8 миллионов долларов. В России джек-пот Всероссийской государственной лотереи (100 миллионов рублей) достался Альберту Бегракяну из Санкт- Петербурга в 2009 году.

Мы провели эксперимент. Группе испытуемых было предложено угадать один из одного, два из двух и три из трёх номеров. В испытании приняли участие 10 человек. Вероятность угадать 1 из 9 номеров равна 1/9 – угадали двое (1/5); два из двух (вероятность 1/90) не угадал никто, при этом трое угадали лишь по одной цифре, три из трёх (вероятность 1/900) никто не угадал, только у троих совпало по одной цифре (Приложение 3).

На запрос «он-лайн лотерея» поступило почти 3 миллиона предложений от Яндекса. Многие мечтают сорвать куш, но наступление этого события маловероятно.

Задача Бюффона по определению числа ?

Известно, что примерное значение ? ? 3,14. Это можно проверить опытным путём, измерив длину любой окружности, её диаметр и вычислив их отношение. Обозначение числа греческой буквой придумал английский математик Джонс, а общепринятым оно стало благодаря Леонарду Эйлеру. Выполняя исследование, мы нашли стихи, позволяющие запомнить цифры этого числа (Приложение 6), обнаружили, что есть разные способы вычисления числа ?, один из них связан с понятием «вероятность». Опираясь на Закон больших чисел, используя случайные величины, в 1777 году Бюффон предложил оригинальный способ для вычисления этой величины. Иглу длины L см бросали многократно на лист бумаги, расчерченный параллельными прямыми через каждые R см, и подсчитывали количество пересечений. P=(2L)/(R?), где Р – отношение количества пересечений к числу бросаний. Отсюда ? = (2L)/(RР). Мы нашли результаты опыта, полученные капитаном Фоксом в 1864 году, и повторили эксперимент, немного его видоизменив. Одновременно бросали по 7 иголок длиной по 3,9 с, а расстояние между прямыми 3,3 см. После первого испытания значение ? ? 4,14 , но после десяти повторений получили ? ? 3,18. (Приложение 4).

Определение площади фигуры методом Монте-Карло.Для иллюстрации метода Монте-Карло, при определении фигуры сложной формы, мы провели компьютерный эксперимент. Допустим, что у нас есть фото такой фигуры, например, болота или острова и нам надо вычислить её площадь. Для этого необходимо расположить объект на прямоугольнике, площадь которого легко найти по формуле S=ab. Далее можно представить, что пошёл снег. Огромное количество снежинок случайным образом падает на прямоугольник и покрывает его вместе с фигурой.

Очевидно, что отношение количества снежинок К1, попавших на прямоугольник так относится к количеству снежинок К2, покрывших фигуру, как площадь прямоугольника S1 относится к площади фигуры S2.

,

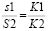следовательно,

.

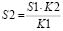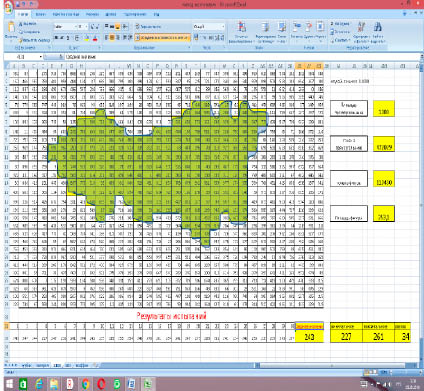
Для создания модели мы применили электронную таблицу MS EXCEL, в которой имеется функция случайное число. По формуле =ОКРУГЛ(СЛЧИС();3)*1000) в каждой клетке таблицы генерируется случайное число от 0 до 1000, обозначающее количество «снежинок» попавших в каждую точку. По формуле =СУММ(A1:AG29) вычислили К1, просуммировали К2 и проведя 30 испытаний, определили среднее значение площади фигуры =СРЗНАЧ(A32:AC32), размах между наибольшим и наименьшим значением. (Приложение 5)

Опыт с семенами

В сельском хозяйстве перед посевом семян всегда проверяют их качество и вычисляют вероятность появления всходов. Мы провели эксперимент. Семена цветов погрузили в стакан с водой. При этом 9 из них ушли на дно, а 3 остались на поверхности, что свидетельствует об их плохом качестве. Все семена мы оставили для проращивания и позже высадили в отдельных горшках. Вероятность всходов была 0,75. Примерно через две недели появились ростки. Причём из 9 «хороших» семян взошло только 8. Наше ожидание оправдалось на 89 %. При этом случилось маленькое чудо. Проросло и одно из бракованных семян. Результат – всхожесть семян совпала с предполагаемой вероятностью (Приложение 6).

Выводы

Изучив источники, мы открыли для себя много новых знаний. Оказывается, привычные для нас предметы были изобретены совершенно случайно, например, мороженое на палочке или микроволновая печь. Наша жизнь состоит из закономерных и случайных событий. При этом, «не все случайности желательны» [9.] Так, по одной из версий, ключ от помещения, где хранились бинокли, был потерян, и команда не смогла заранее увидеть айсберг, ставший причиной гибели «Титаника».

На каждой упаковке с лекарствами указывают вероятность наступления аллергической реакции. Например, в одном из ста случаев. Ежедневно мы слушаем прогнозы метеорологов, где уместно использовать слова «вероятно, что завтра будет дождь». Благодаря тому, что наука не стоит на месте, эти прогнозы всё чаще сбываются.

Беседуя с продавцами, мы выяснили, что даже в магазине вероятность продаж, зависит от расположения продуктов на полках. Чаще покупают товары, расположенные ближе к кассам и на уровне глаз покупателей. Именно поэтому товары в больших магазинах часто перекладывают с места на место.

Вероятность получения хорошей оценки на контрольной работе по математике ?=0,25 но может случиться всякое. Хотя, чем лучше вы к ней приготовитесь, тем выше шанс оправдать ожидание. По словам Д. Мойеса: «Теория вероятности и Закон больших чисел утверждают: иногда нужно пытаться снова и снова, чтобы получить желаемый результат. Чем больше пытаешься, тем скорее получится…в сущности, иногда просто надо не сдаваться» [11].

Поставив эксперименты, мы проверили действие Закона больших чисел. Действительно, только при большом количестве испытаний оправдывается математическое ожидание, хотя бывают и исключения.

В опыте с игральной костью вероятность выпадения любой из шести цифр примерно совпала с частотой выпадения и угадывания цифры только при достаточно большом количестве бросаний.

В опыте с иглой, мы получили результат с точностью только до десятых, так как провели слишком мало повторений.

В опыте с семенами математическое ожидание совпало с результатом эксперимента полностью. При вероятности 0,78 проросли 75 % семян.

Мы проверили экспериментально, что шанс выиграть в лотерее ничтожно мал.

С помощью электронной таблицы нам удалось вычислить площадь фигуры методом Монте-Карло.

Главный вывод, к которому мы пришли, заключается в том, что вероятностный подход применяется практически во всех сферах деятельности. (Приложение 7) Какую бы профессию человек ни выбрал, чем бы ни занимался, ему необходимы элементарные знания по этой теме. Наша гипотеза подтвердилась. Вероятность – одно из важнейших понятий, как в современной науке, так и жизни человека. Вероятностный подход применяется практически во всех сферах человеческой деятельности.

Мы выполнили все поставленные задачи. Цель исследования достигнута.

Приложения

Приложение 1

Таблица 1

Приложение 2

Таблица 2

Приложение 3

Таблица 3

Приложение 4

Таблица 4

Приложение 5

Компьютерный эксперимент. Метод Монте-карло

Таблица 6

Приложение 6

Приложение 7

Таблица 6

Словарь терминов

Тео?рия вероя?тностей – раздел математики, изучающий: случайные события, случайные величины, их свойства и операции над ними.

В теории вероятностей Зако?н больши?х чи?сел (ЗБЧ) это принцип, который описывает результат выполнения одного и того же эксперимента много раз. Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения.

Веро?ятность (матем.), числовая характеристика степени возможности появления случайного события , могущего повторяться неограниченное число раз.

Вероятностью некоторого случайного события называется отношение количества благоприятных исходов к общему количеству исходов испытания.

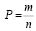
Случайная величина (СВ) – это численная характеристика, измеряемая по ходу опыта и зависящая от случайного исхода.

Событие называется невозможным, если оно не может произойти в условиях данного опыта Р=0.

Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться.

События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие.

Частота события – отношение появления события к количеству возможных исходов.

Библиографическая ссылка