Теория уравнений занимает ведущее место в алгебре и математике в целом. Значимость ее заключается не только в теоретическом значении для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
В школьной программе рассматривается только 3 способа их решения. Готовясь к предстоящим экзаменам, я заинтересовался другими способами их этих уравнений. Поэтому я выбрал тему «10 способов решения квадратных уравнений».
Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, что также пригодится и при решении более сложных задач, в том числе и при сдаче экзаменов.
Цель работы: изучить различные способы решения квадратных уравнений, научиться решать квадратные уравнения.
Задачи:
– рассмотреть стандартные и нестандартные методы решения квадратных уравнений;
– выявить наиболее удобные способы решения квадратных уравнений;
– научиться решать квадратные уравнения различными способами.
Объект исследования: квадратные уравнения.
Предмет исследования: способы решения квадратных уравнений.
Методы исследования:
- теоретические: изучение литературы по теме исследования, изучение тематических Интернет-ресурсов;
- анализ полученной информации;
- сравнение способов решения квадратных уравнений на удобство и рациональность.
Методы решения квадратных уравнений
Квадратным уравнением называется уравнение вида ax2 + bx + c = 0, где х – переменная, a, b и с – некоторые числа, при этом а ? 0. Корень такого уравнения – это значение переменной, обращающее квадратный трёхчлен в ноль, то есть значение, обращающее квадратное уравнение в тождество. Коэффициенты квадратного уравнения имеют собственные названия: коэффициент а называют первым или старшим, коэффициент b называют вторым или коэффициентом при х, с называется свободным членом этого уравнения.
Полным квадратным уравнением называют такое, все коэффициенты которого отличны от нуля (a, b, c - 0).
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент а: x2 + px + q = 0, р = b/a, q = c/a.
Неполные квадратные уравнения бывают трёх видов:
1) ax2 + c = 0, где с - 0;
2) ax2 + bx = 0, где b - 0;
3) ax2= 0.
В рамках данной работы мы будем рассматривать способы решения только полных квадратных уравнений.
Решение квадратных уравнений по общей формуле
Для решения квадратных уравнений применяется способ нахождения корней через дискриминант. Для нахождения дискриминанта используется следующая формула D = b2 – 4ac. После нахождения D мы используем формулу для нахождения корней уравнения
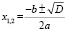 .
.
Стоит заметить, что если:
D > 0 – уравнение имеет два корня;
D = 0– уравнение имеет один корень;
D < 0 – уравнение не имеет корней.
Пример решения уравнения данным способом показан на рис. 1(1.1).
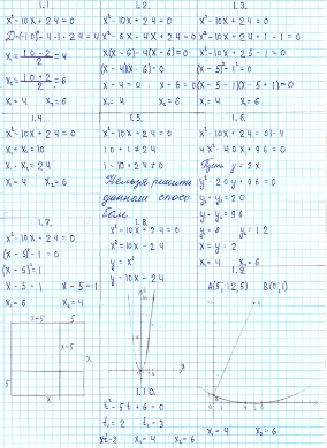
Рис. 1. Практическая часть
Разложение левой части на множители
Для демонстрации способа решим уравнение x2 + 10x – 24 = 0.
Разложим левую часть на множители:
x2 + 10x – 24 = x + 12x – 2x – 24 = = x(x + 12) – 2(x + 12) = (x + 12)(x – 2).
Следовательно, уравнение можно переписать так:
(x + 12) (x – 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при x = 2, а также при x = –12.
Пример решения уравнения данным способом показан на рис. 1(1.2).
Метод выделения полного квадрата
Выделение полного квадрата – это такое тождественное преобразование, при котором заданный трехчлен представляется в виде (a ± b)2 суммы или разности квадрата двучлена и некоторого числового или буквенного выражения.
Решим уравнение x2 + 14x + 40 = 0.
Решение:
Разложим многочлен на множители методом выделения полного квадрата.
Для применения первой формулы необходимо получить выражение
x2 + 14x + 49 = 0.
Поэтому прибавим и отнимем от многочлена x2 + 14x + 40 число 9, чтобы выделить полный квадрат
x2 + 14x + 40 + 9 – 9 = 0
(x + 14x + 40 + 9) – 9 = 0
(x + 14x + 49) – 9 = 0
(x + 7)2 – 9 = 0
Применим формулу «разность квадратов» a2 – b2 = (a – b)·(a + b)
(x + 7)2 – 32 = 0
(x + 7 – 3)(x + 7 + 3) = 0
(x + 4)(x + 10) = 0
x + 4 = 0x + 10 = 0
x1 = – 4x2 = – 10
Ответ: –4; – 10.
Пример решения уравнения данным способом показан на рис. 1(1.3).
Решение уравнений с помощью теоремы Виета
Для решения полного квадратного уравнения по теореме Виета нужно разделить всё уравнение на коэффициент а. Для уравнения x2 + px + q = 0, если х1 и х2 его корни, справедливы формулы:
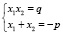
Пример решения уравнения данным способом показан на рис. 1(1.4).
Решение уравнений с использованием свойств коэффициентов
Если выполняется следующее условие: а + с = b, то x1 = – 1; x2 = – с/а.
Пример:
4x2 + 3x – 1 = 04 – 1 = 3
x1 = – 1x2 = – 1/4
x2 = – 0,25
Если выполняется следующее условие:
а + b + c = 0, то x1 = 1; x2 = с/а.
Пример:
5x2 + 2x – 7 = 05 + 2 –7 = 0
x1 = 1x2 = 7/5
x2 = 1,2
Пример невозможности решения уравнения данным способом показан на рис. 1(1.5).
Решение уравнений способом «переброски»
Так называемый метод «переброски» позволяет сводить решение неприведённых и непреобразуемых к виду приведённых с целыми коэффициентами путём их деления на старший коэффициент уравнений к решению приведённых с целыми коэффициентами. Он заключается в следующем: умножим уравнение ax2 + bx + с = 0 на а.
Получим: a2x2 + abx + aс = 0. Введём новую переменную y = ax. Получим y2+by+ac = 0. Корни этого уравнения y1 и y2.Следовательно х1 = y1/a; х2 = y2/a.
Пример решения уравнения данным способом показан на рис. 1(1.6).
Геометрический способ решения квадратных уравнений
Решим уравнение x2 – 4x – 12 = 0.
Представим его в виде x2 – 4x = 12.
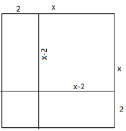
Рис. 2
На рис. 2 «изображено» выражение x – 4x, т.е. из площади квадрата со стороной х дважды вычитается площадь квадрата со стороной 2. Значит х2 – 4х + 4 есть площадь квадрата со стороной х – 2.
Выполнив замену x2 – 4x = 12, получим
(x – 2)2 = 12 + 4
(x – 2)2 = 16
x – 2 = 4x – 2 = – 4
x1 = 6 x2 = – 2
Ответ: x1 = 6, x1 = – 2.
Пример решения уравнения данным способом показан на рис. 1(1.7).
Графическое решение квадратного уравнения
В уравнении x2 + px + q = 0 перенесём второй и третий члены в правую часть уравнения. Получим: x2 = – px – q. Построим графики функций
y = x2 (парабола);
y = – qx – p (прямая).
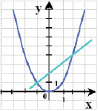
Рис. 3
Следует учесть, что:
– если прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
– если прямая касается параболы (только одна общая точка), то уравнение имеет один корень;
– если прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Пример решения уравнения данным способом показан на рис. 1(1.9).
Решение уравнения при помощи циркуля и линейки
Решим уравнение ax2 + bx + c = 0:
1) построим на координатной плоскости точки:
A(– b/2a; (a + c)/2a) – центр окружности и В(0; 1)
2) Проведём окружность r = AB
3) Абсциссы точек пересечения с осью Ox есть корни исходного уравнения
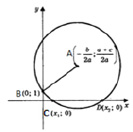
Рис. 4
Следует учесть, что:
– если радиус окружности больше ординаты центра (AB > АС, или R > (a + c)/2a), окружность.
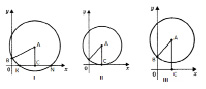
Рис. 5
Пересекает ось абсцисс в двух точках К(х1; 0) и N(х2; 0), где х1 и х2 – корни квадратного уравнения x2 + bx + c = 0.
– если радиус окружности равен ординате центра (AB = AС, или R = (a + c)/2a), окружность касается оси абсцисс в точке С(х ; 0), где х1 – корень квадратного уравнения.
– если радиус окружности меньше ординаты центра (AB < AС, или R < (a + c)/2a), окружность не имеет общих точек с осью абсцисс, в этом случае уравнение не имеет решения.
Пример решения уравнения данным способом показан на рис. 1(1.9).
Решение квадратных уравнений с помощью номограммы
Это старый и в настоящее время забытый способ решения квадратных уравнений.
Номограмма даёт значения положительных корней уравнения z2 + pz + q = 0. Если уравнение имеет корни разных знаков, то, найдя по номограмме положительный корень, отрицательный находят, вычитая положительный из – р.
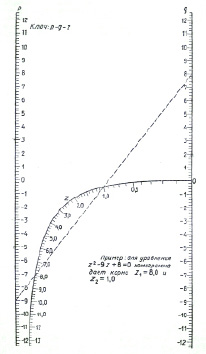
Рис. 6. Вид монограммы для решения уравнения z2 + pz + q = 0
В случае, когда оба корня отрицательны, берут z = – t и находят по номограмме два положительных корня t1; t2 уравнения t2 + – pt + z = 0, а затем z1 = – t1; z2 = – t2.
Если коэффициенты p и q выходят за пределы шкал, выполняют подстановку z = kt и решают посредством номограммы уравнение
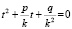 ,
,
где k берётся с таким расчётом, чтобы имели место неравенства
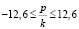 ;
; 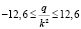 .
.
Вид монограммы для решения уравнения z2 + pz + q = 0 можно найти на рис. 6.
«Плюсы» и «минусы» различных способов решения
|
Название способа решения квадратных уравнений |
Плюсы |
Минусы |
|
Решение квадратных уравнений по формуле |
Можно применить ко всем квадратным уравнениям. |
Нужно выучить формулы. |
|
Разложение левой части уравнения на множители |
Дает возможность сразу увидеть корни уравнения. |
Нужно правильно вычислить слагаемых для группировки. |
|
Метод выделения полного квадрата |
За минимальное количество действий можно найти корни уравнений |
Нужно правильно найти все слагаемые для выделения полного квадрата. |
|
Решение уравнений с использованием теоремы Виета |
Достаточно легкий способ, дает возможность сразу увидеть корни уравнения. |
легко находятся только целые корни. |
|
Свойства коэффициентов квадратного уравнения |
Не требует особых усилий |
Подходит только к некоторым уравнениям |
|
Решение уравнений способом переброски |
За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета. |
легко найти только целые корни. |
|
Геометрический способ решения квадратных уравнений |
Наглядный способ. |
похож на способ выделения полного квадрата |
|
Графическое решение квадратного уравнения |
Наглядный способ |
Могут быть не точности при составлении графиков |
|
Решение квадратных уравнений с помощью циркуля и линейки |
Наглядный способ |
Могут быть не точности |
|
Решение квадратных уравнений с помощью номограммы |
Наглядный способ, прост в применении. |
Не всегда под рукой имеется номограмма. |
Заключение
В ходе выполнения данной исследовательской работы мне удалось обобщить и систематизировать изученный материал по выбранной теме, изучить различные способы решения квадратных уравнений, научиться решать квадратные уравнения 10 способами. Нужно отметить, что не все они удобны для решения, но каждый из них по-своему интересен. С моей точки зрения, наиболее рациональными для использования будут способы, изучаемые в школе: 1.1. (по формуле); 1.4. (по теореме Виета); а также способ 1.5. (используя свойства коэффициентов).
Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в математике. Эти знания могут пригодиться нам не только в школе и в ВУЗе, но и на протяжении всей жизни.
Библиографическая ссылка
Улевский С.А. ДЕСЯТЬ СПОСОБОВ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ // Старт в науке. 2016. № 1. ;URL: https://science-start.ru/ru/article/view?id=15 (дата обращения: 05.02.2026).
