Уравнение вида y = kx + b задается как парой переменных x и y, так и парой параметров k, b. Поэтому возник вопрос, возможно ли изобразить прямую из плоскости ху соответствующим ей объектом в плоскости параметров (k; b), что будет представлять собой этот объект, как будут изображены семейства прямых со схожими свойствами.
Цели работы:
1) отображение графиков линейных функций на плоскости параметров;
2) определение семейства прямых, отображенных на плоскости параметров в виде прямых или областей;
Задачи работы:
1) научиться выполнять построения графиков линейных функций на плоскости параметров, и наоборот, уметь выполнить построение графика в плоскости ху по соответствующему объекту из плоскости параметров аb;
2) выяснить, какие семейства прямых из плоскости ху изображаются на плоскости параметров в виде прямых, в виде областей;
3) обобщить полученные результаты для правил построения любого семейства прямых.
Гипотеза:
Если прямые на плоскости (x; y) пересекаются в одной точке или параллельны, то соответствующие им точки на плоскости (k; b) лежат на одной прямой.
Методы исследования:
1) экспериментальный;
2) аналитико – синтетический.
Предмет исследования: отображение графиков линейных функций на плоскость параметров (k, b).
Объект исследования: график линейной функции.
Семейства прямых на координатной плоскости (х; у), соответствующих точкам плоскости (k; b)
Линейным уравнением с двумя переменными называется уравнение вида y = kx + b, где x и y – переменные, k, b – некоторые числа.
Графиком линейного уравнения с двумя переменными является прямая.
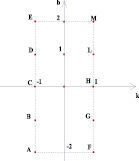
Рассмотрим координатную плоскость (k; b). Каждая прямая вида у = kх + b изображается на этой плоскости в виде точки с координатами (k; b).
Например, прямая у = 2х + 5 изображается на плоскости (k; b) в виде точки (2; 5), а прямая у = – 2 в виде точки (0; – 2).
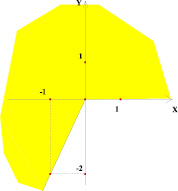
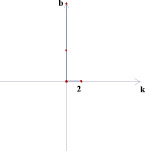
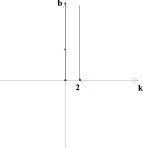
Выполняя построения графиков линейных функций на плоскости параметров, было замечено, что параллельные прямые отображаются на этой плоскости в виде точек, лежащих на одной прямой, перпендикулярной оси Оk (рис. 1).
Плоскость (x; y) Плоскость (k; b)
Рис. 1
Действительно, у точек, лежащих на таких прямых координата k одинакова, а это коэффициент при х, по которому можно определить взаимное расположение графиков прямых на плоскости (x; y).
Чем ближе вертикальные прямые к началу координат, тем меньше угол наклона между возрастающими прямыми и осью Ох и больше угол наклона между убывающими прямыми и осью Ох (рис. 2).
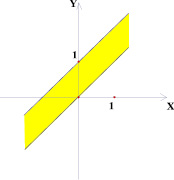
Рис. 2
Раскрашенные области
На плоскости, кроме точек и прямых, можно изображать области (будем их выделять цветом).
Рассмотрим следующую задачу: на координатной плоскости (k; b) изображено множество точек, соответствующее некоторому семейству прямых вида у = kх + b. На плоскости (х; у) все эти прямые покрашены. Изобразить на плоскости (х; у) получившуюся покрашенную область. Были получены следующие результаты (рис. 2–7).
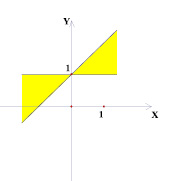
Рис. 3
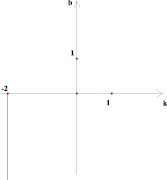
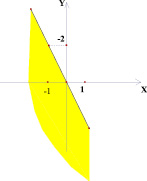
Рис. 4
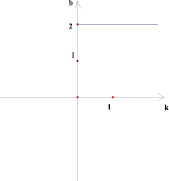
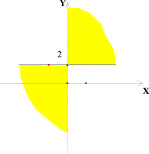
Рис. 5
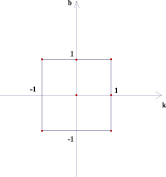
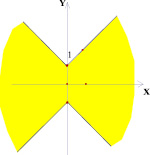
Рис. 6
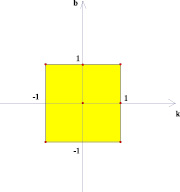
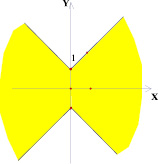
Рис. 7
Точки внутри квадрата на плоскости (k; b) в 5 и 6 случае имеют одинаковые закрашенные области на плоскости (х; у), потому что любая точка внутри квадрата лежит на отрезке, параллельном оси абсцисс плоскости (k; b) с концами на сторонах квадрата. На плоскости (х; у) это будет означать, что соответствующая выбранной точке прямая будет лежать в полосе между прямыми, соответствующими концам отрезка, то есть в покрашенной области.
Исследуем обратную задачу: на координатной плоскости (х; у) покрашено некоторое семейство прямых. В результате на плоскости получилась покрашенная область. Изобразите на координатной плоскости (k; b) множество точек, соответствующее этому семейству прямых. Оказывается, в некоторых случаях это можно сделать не единственным образом (рис. 8–9).
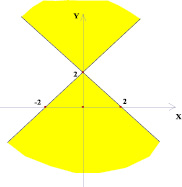
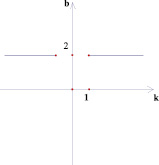
Рис. 8
|
|
или
|
Рис. 9
Как видно из рис. 9 возможно несколько решений. Например, объединение луча (полуоси ординат в положительном направлении) и отрезка [0; 2] на оси абсцисс. Или объединение двух лучей: полуоси ординат в положительном направлении и параллельного луча с вершиной в точке (2; 0).
Прямая на плоскости (k; b)
Рассмотрим на плоскости (k; b) прямую b = k. Каждая точка этой прямой задает на плоскости (х; у) прямую, а вся прямая b = k задает на плоскости (х; у) семейство прямых. Для определения свойства семейства прямых сначала были взяты несколько конкретных точек на прямой b = k и построены соответствующие им прямые на плоскости (х; у). Оказалось, что все прямые проходят через точку (– 1; 0).
Докажем это утверждение. Так как b = k, то на плоскости (х; у) мы получаем семейство прямых вида у = kx + k. Если записать их в виде у = k(x + 1), то можно заметить, что все эти прямые проходят через точку (– 1; 0).
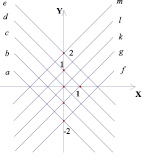
На координатной плоскости (k; b) проведем три прямые, проходящие через одну точку. Каждая такая прямая изображает пучок прямых на плоскости (х; у). Три точки на плоскости (х; y), через которые проходят соответствующие пучки прямых, сами лежат на одной прямой.
На координатной плоскости (k; b) проведем три параллельные прямые. Каждая такая прямая изображает некоторое семейство прямых на плоскости (х; у). Три точки на плоскости (х; y), через которые проходят соответствующие пучки прямых, также лежат на одной прямой.
В случае пересечения три точки лежат на наклонной прямой, а в случае параллельности прямая вертикальна.
Можно сделать вывод, что три параллельные прямые и три прямые, имеющие общую точку, ведут себя одинаково (их образы лежат на одной прямой). Если договориться считать, что параллельные прямые также имеют общую точку – бесконечно удалённую, то не надо будет рассматривать эти два случая отдельно.
Заключение
В ходе исследования были выполнены построения графиков линейных функций на плоскости параметров, и наоборот, выполнены построения графика в плоскости (х; у) по соответствующему объекту из плоскости параметров (k; b). Графики и их образы выполнялись как вручную, так и с помощью программы «Математический конструктор».
Были сделаны следующие выводы:
– семейство пересекающихся прямых в одной точке из плоскости (х; у) изображается на плоскости параметров в виде прямой;
– замкнутая область из плоскости параметров представляет собой закрашенную область, ограниченную двумя парами пресекающихся прямых;
– образы параллельных прямых лежат на одной прямой, перпендикулярной оси Оk в плоскости параметров.
Одинаковое поведение образов параллельных прямых и прямых, имеющих общую точку (лежат на одной прямой), позволяет не рассматривать эти случаи отдельно, если считать, что параллельные прямые также имеют общую точку – бесконечно удалённую.
Было доказано, что прямая b = k задает на плоскости (х; у) семейство пересекающихся прямых, проходящих через точку (– 1; 0).
Предположение о том, что если прямые на плоскости (x; y) пересекаются в одной точке или параллельны, то соответствующие им точки на плоскости (k; b) лежат на одной прямой, подтвердилось.
Результаты исследования можно использовать на факультативных занятиях в старших классах при введении понятия проективной плоскости, а также для углубленного изучения свойств графиков линейной функции.
Планируется создать программу для построения образов линейной функции на плоскости параметров и для обратной задачи.
Библиографическая ссылка
Сугаков Р.В. ИССЛЕДОВАНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ ВИДА Y = KX + B НА ПЛОСКОСТИ ПАРАМЕТРОВ (K; B) // Старт в науке. 2016. № 1. ;URL: https://science-start.ru/ru/article/view?id=14 (дата обращения: 05.02.2026).