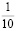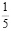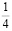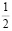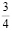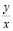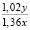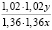Проценты встречаются в нашей жизни ежедневно: мы сталкиваемся с повышением зарплаты, ростом уровня инфляции, цен на нефть, на коммунальные услуги. Проценты встречаются в хозяйственных и финансовых расчётах, статистике, науке и технике, здравоохранении и образовании. Планирование семейного бюджета, крупные покупки (техника, недвижимость), связанные с кредитованием – всё это стало обычным явлением. Неумение решать задачи на проценты может обернуться для людей финансовыми потерями. Если человек не вносит своевременно плату за коммунальные услуги, или не платит вовремя кредит или налоги, на него налагается штраф – “пеня”. Он рассчитывается согласно законодательству Российской Федерации, как определенный процент от суммы коммунальных услуг за каждый просроченный день.
В курсе школьной математики проценты изучаются только в 4 четверти 5 класса, а в заданиях Основного Государственного Экзамена и Единого Государственного Экзамена встречаются достаточно часто. Например, с 2016 года в заданиях второй части ЕГЭ появилась задача № 17 с экономическим содержанием, с которой, согласно статистико-аналитическому отчёту о результатах ЕГЭ в 2017 году справились 5,3 % участников.
Поскольку в будущем я планирую поступить в университет, меня заинтересовали задачи на проценты, я сделал подборку задач из Открытого банка заданий ОГЭ и ЕГЭ и постарался разобраться с основными способами решения задач на проценты.
Цель исследования:
1. Изучение литературы по данной теме в печатном и электронном виде
2. Изучение истории возникновения процентов, понятия процента, процентного отношения, схем решения задач с процентами
3. Отработка полученных знаний в ходе решения задач из открытого банка заданий огэ и егэ по математике
4. Ознакомление обучающихся 6–11 классов с применением процентов в ходе решения задач из ОГЭ и ЕГЭ.
Объект исследования: процентные отношения.
Предмет исследования – практические задачи на проценты из Открытого банка заданий ЕГЭ и ОГЭ по математике.
Методы исследования:
1. Изучение литературы
2. Выполнение практических заданий
3. Сравнение и обобщение полученных результатов.
Практическая значимость: использование материала при подготовке к олимпиадам и государственной итоговой аттестации.
Новизна проведённой исследовательской работы: изучение методов решения задач с использованием процентного отношения, встречающихся среди заданий № 17 Единого государственного экзамена, как выходящих за рамки программы по математике 5 класса.
Выдвинута гипотеза: формула сложных процентов помогает решить задачи с экономическим содержанием.
1. Теоретическая часть
1.1. История возникновения понятия «процент»
Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще у жителей древнего Вавилона. Но самое широкое распространение проценты получили в Древнем Риме.
Римляне называли процентами деньги, которые платил должник кредитору за каждую сотню. От римлян проценты перешли к другим народам Европы.
Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/). Так возник современный, привычный для нас символ для обозначения процента.
Таким образом, один процент от величины равен одной сотой данной величины.
В жизни многие величины связаны процентным отношением – один процент от центнера равен одному килограмму, один процент от метра – одному сантиметру, один процент от гектара – одному ару.
1.2. Основные типы задач на проценты
Задачи на проценты можно разделить на три основных группы:
1. Нахождение процентов от числа.
Чтобы найти проценты от числа, нужно проценты превратить в десятичную дробь и умножить на это число.
Пример 1. (№2564, «3000 заданий для подготовки к ОГЭ»)
Средний вес мальчиков того же возраста, что и Саша, составляет 55 кг. Вес Саши равен 110 % среднего веса. Сколько килограммов весит Саша?
55•110 : 100 = 55 • 1,1 = 60,5 (кг).
Ответ 60,5 кг.
Очень удобно превращать проценты в десятичную или обыкновенную дробь.
Таблица 1
|
Проценты |
Десятичная дробь |
Обыкновенная дробь |
|
10 % |
0,1 |
|
|
20 % |
0,2 |
|
|
25 % |
0,25 |
|
|
50 % |
0,5 |
|
|
75 % |
0,75 |
|
Например, для нахождения 50 % от числа достаточно разделить его на 2 и получить нужный результат. Для нахождения 20 % от числа достаточно разделить его на 5. Эти приёмы очень упрощают вычисления и позволяют избежать ошибок.
Предыдущий пример можно решить так:
55+ 0,1 • 55 = 60,5 (кг).
2 тип задач на проценты: нахождение числа по его процентам.
Чтобы найти число по его процентам, нужно проценты превратить в десятичную дробь и число разделить на эту дробь.
Пример 2 . .(№2612 , «3000 заданий с ответами для подготовки к ОГЭ»)
В ходе распродажи после снижения цены на 20 % товар стал стоить 600 рублей. Какова была цена товара до распродажи?
Если взять исходную цену за 100 %,то новая цена составит 100 % – 20 % = 80 %.
600 : 0,8 = 750 (рублей).
Ответ: 750 руб.
3 тип задач на проценты: нахождение процентного отношения чисел.
Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100.
Пример 3. (№ 2616 , «3000 заданий с ответами для подготовки к ОГЭ»)
Магазин делает пенсионерам скидку на определённое количество процентов от стоимости покупки. Пакет сока стоит в магазине 40 рублей, а пенсионер заплатил за сок 34 рубля. Сколько процентов составляет скидка для пенсионера?
Решение: Скидка составила 6 рублей. Найдем процентное отношение:
6 : 0,4 = 15 %.
Ответ: 15 %.
Иногда бывает удобным сравнивать две величины не по разности их значений, а в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного товара больше или меньше цены другого в процентах
Мною было проведено анкетирование среди обучающихся 7,10 и 11 классов. Предлагались 3 задачи на проценты согласно типам плюс для 10–11 кл вопрос об умении решать задачу № 17. Итоги анкетирования приводятся в таблице.
Таблица 2
|
Класс |
Количество опрошенных |
1 тип |
2 тип |
3 тип |
№17 (только для 10–11 кл) |
|
7 |
18 |
14 (78 %) |
12 (67 %) |
11 (61 %) |
- |
|
10 |
12 |
12 (100 %) |
11 (92 %) |
10 (83 %) |
3 (25 %) |
|
11 |
11 |
11 (100 %) |
9 (82 %) |
9 (82 %) |
2 (18,1 %) |
На основании этого можно сделать вывод, что данные по старшей школе соответствуют данным статистико-аналитического отчёта о результатах ЕГЭ за 2017 год, согласно которому задачу на проценты 1 типа верно решили среди сдающих базовый уровень 93,5 % участников, профильный уровень – 96,2 % участников. Малое количество умеющих решать задание № 17 в 10–11 классах обусловлено тем, что в 11 классе 45 % опрошенных сдают базовый уровень, в 10 классе 50 % опрошенных планируют сдавать базовый уровень.
Несмотря на то, что решение задач, связанных с процентами, достаточно просто, ошибки возникают чаще всего при подсчёте процентов от разных величин.
Очень часто встречаются задачи на проценты, связанные с банковским делом и кредитами.
1.3. Формула сложных процентов
Сложным процентом принято называть эффект, когда проценты прибыли прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли. Формула сложного процента – это формула, по которой рассчитывается итоговая сумма с учётом начисления процентов.
s = s0(1+0,01p)n,
s0 – начальная сумма, р – процентная ставка, n – время.
Пример 4. (Открытый банк заданий ЕГЭ).
По пенсионному вкладу банк выплачивает 12 % годовых. По истечению каждого года начисленная сумма присоединяется к вкладу. На данный вид вклада был открыт счёт на 100000 рублей, который не пополнялся и с которого не снимались деньги в течение двух лет. Какой доход был получен по истечении этого срока?
Решение: Эту задачу можно решить двумя способами:
1 способ:
1) 1000000*0,12=12000 (руб.) – доход за 1 год
2) 100000+12000=112000 (руб.) – будет на счету по окончании 1 года.
3) 112000* 0,12=13440 (руб.) – доход за 2 год .
4) 112000 + 13440 = 125440 (руб.) – на счету по окончании 2 года
5) 125440 – 100000=25440 (руб).
ОТВЕТ: по истечении двух лет получился доход в размере 25440 руб.
2 способ :воспользуемся формулой сложных процентов: Пусть: s = 100000 начальный вклад p= 12 % годовых n = 2 года, получим:
100000(1+ 0,12)2 = 100000•1,122 = =125440 руб.
Этим узнали конечную сумму на счету после двух лет. Сумма дохода за 2 года составит
125440– 100000=25440 руб.
Ответ: по истечении срока был получен доход в размере 25440 руб.
Делаем вывод, что с использованием формулы сложных процентов данная задача решается быстрее.
Практическая часть
Задача 1 (Тренировочный вариант ОГЭ № 165, №7)
Молоко дает 22 процента сливок, сливки дают 25 процентов масла. Сколько масла получится из 300 кг молока?
Решение: эту задачу легче решить, переведя проценты в десятичные дроби
300• 0,22 •0,25 = 16,5 (кг)/
Ответ: 16,5 кг.
Задача 2 (тренировочный вариант ЕГЭ (математика, профильный уровень, №11))
7 одинаковых рубашек дешевле куртки на 2 %. На сколько процентов 10 этих же рубашек дороже куртки?
Решение: Взяв цену куртки за 100 %,мы найдем цену 7 рубашек: 100 – 2= 98 %
Одна рубашка составляет по 98 : 7 = 14 % цены куртки
10 рубашек стоят 140 % от цены куртки, следовательно, 140–100=40 % Ответ: на 40 %.
Задача 3 (Тренировочный вариант 215, задача № 17(3 балла)).
Сумма вклада увеличивалась первого числа каждого месяца на 2 % по отношению к сумме на первое число предыдущего месяца. Аналогично, цена на кирпич возрастала на 36 % ежемесячно. Отсрочив покупку кирпича,1 мая в банк под проценты положили некоторую сумму. На сколько процентов меньше в этом случае можно купить кирпича на 1 июля того же года на всю сумму, полученную из банка вместе с процентами?
Решение:
Таблица 3
|
Цена 1 кирпича, у.е. |
Сумма денег, у.е. |
Количество кирпичей, шт. |
|
|
1.05. |
x |
y |
|
|
1.06 |
1.36x |
1.02y |
|
|
1.07. |
1.36•1.36x |
1.02•1.02y |
|
Учитывая, что 1,02² =1,0404 1,36² = 1,8496 ,найдем отношение количества кирпичей, которые можно было купить 1 июля, к количеству кирпичей, которые можно было купить
1 мая:
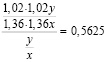 .
.
Это составляет 56,25 %. Следовательно, к указанной дате можно купить на 100 % –56,25 % = 43,75 % меньше кирпича, двумя месяцами раньше.
Ответ: на 43,75 %.
Задача 4 (математика, № 11, профильный уровень).
Собрали 4 кг свежих цветков ромашки, влажность которых 90 %. После того, как цветки высушили, их влажность составила 20 %. Чему равна масса цветков ромашки после сушки?
Решение. Решение подобных задач основано на условном разделении объекта на воду и так называемое «сухое вещество», масса которого при любых условиях не меняется.
Таблица 3
|
Масса, в кг |
Содержание, в % |
||
|
воды |
Сухого вещества |
||
|
Свежие цветы |
4 |
90 |
100 – 90 = 10 |
|
Высушенные цветы |
х |
20 |
100 – 20 = 80 |
1) 0,1 · 4 = 0,4 (кг) – масса сухого вещества в 4 кг
2) Составим пропорцию
0,4 кг – 80 %
x кг – 100 %
Отсюда, х = 0,4 · 100 : 80 = 0,5 (кг).
Ответ: 0,5 кг.
Заключение
1. Изучив литературу по теме, я ознакомился с понятием процента как частного вида десятичных дробей, научился решать задачи на проценты, в том числе и с формулой сложных процентов
2. Подтверждена необходимость уметь решать задачи с процентами в повседневной жизни, а также для успешной сдачи ОГЭ и ЕГЭ.
3. Проведено анкетирование, составлена таблица по результатам опроса.
4. В ходе оформления работы я научился работать с математическими формулами в текстовом редакторе Word.
Проценты дают возможность легко сравнивать между собой части целого, упрощают расчёты и поэтому очень распространены.
В ходе своего исследования я убедился в том, что проценты дают возможность легко сравнивать между собой части целого, упрощают расчёты. При решении более сложных задач на проценты вместо того, чтобы применять стандартные способы, целесообразней воспользоваться формулой сложных процентов, что подтверждает выдвинутую мной гипотезу.
В будущем я планирую продолжить изучение задач, связанных с процентами.
Библиографическая ссылка
Лахтионов Н.С. ЗАДАЧИ НА ПРОЦЕНТЫ В ОГЭ И ЕГЭ // Старт в науке. 2018. № 5-6. ;URL: https://science-start.ru/ru/article/view?id=1222 (дата обращения: 03.03.2026).