В современном мире, в век развития новых технологий и компьютерной техники люди проявляют меньше желания использовать собственные умственные способности в осуществлении действий с числами.
Компьютеры, калькуляторы, планшеты, ноутбуки, смартфоны основательно вошли в нашу жизнь, но, несмотря на это, потребность развивать и совершенствовать свои природные задатки у человека становится еще более актуальной, чем когда-либо. Ведь по сей день гибкость ума является предметом гордости, а способности производить вычисления в уме вызывают откровенное удивление людей.
Мы используем навыки умственных математических вычислений ежедневно во всех сферах нашей жизни. Они помогают детям и взрослым правильно посчитать сдачу в магазине, прикинуть в уме график будущих выплат при крупной покупке в кредит, планировать семейный бюджет.
«Математика – царица наук» – это выражение мы знаем с первого класса. Математика – один из самых важных предметов в школе. Я еще не знаю, какую профессию выберу в будущем, но твёрдо уверена, что математика необходима в жизни любого человека: оплата за квартиру (за коммунальные услуги), покупки и расчет в магазинах, оплата за проезд и т.д. Не стоит забывать, что через несколько лет мне и моим одноклассникам предстоит сдавать экзамены по математике, а для успешной сдачи нужно хорошо уметь считать.
Я неоднократно наблюдала ситуацию, когда человек долго стоит в магазине у какой-нибудь витрины, считая сумму всей покупки, или, ученик мучается с вычислением сложного примера, когда до звонка остается мало времени. Это говорит о том, что люди затрудняются в устных вычислениях. Своей научно-исследовательской работой я хочу помочь ученикам школ научиться быстро и правильно считать.
Данная научно-исследовательская работа направлена на ознакомление и овладение приёмами быстрого счета, которые могут применяться в учебной деятельности и в жизни. При работе были рассмотрены вопросы: когда появились вычисления рассмотрены приёмы быстрого счёта, которые легко запомнить и применять на уроках и в жизни и др., был создан буклет «Приёмы быстрого счета» (для тех, кто хочет быстро считать в уме).
Цель научно-исследовательской работы – изучение и освоение некоторых приёмов быстрого счёта, которые могут применяться в учебной деятельности и в жизни.
Задачи научно-исследовательской работы:
– найти и изучить информацию по теме «Приёмы быстрого счёта»
– освоить несколько приёмов быстрого счёта, которые могут применяться в учебной деятельности и в жизни
– создать буклет о приёмах быстрого счета, которые могут быть применимы в учебной деятельности и в жизни.
Методы, применяемые при выполнении научно-исследовательской работы: анкетирование, работа с источниками информации, анализ, сравнение и систематизация полученной информации, наблюдение.
Достигнутые результаты: изучение информации по теме «Приёмы быстрого счёта» освоение некоторых приёмов быстрого счета и ознакомление с ними одноклассников создание буклета «Приёмы быстрого счёта» (для тех, кто хочет быстро считать в уме) применение некоторых приёмов быстрого счёта в учебной деятельности и в жизни.
Несмотря на то, что тема научно-исследовательской работы неоднократно рассматривалась в различных информационных источниках (интернете, журналах, статьях) и степень её изученности достаточно высока, считаю данный вопрос интересным, актуальным и применимым на практике.
Из истории счёта и вычислительных приёмов
Трудно ответить на вопросы, когда появились первые вычисления. Но все знают, что с древнейших времен у человека возникла потребность подсчитывать количество добычи или урожая, измерять земельные участки, определять вместимость сосудов, вести счёт времени. Наши далекие предки часто сталкивались с необходимостью делить продукты, добычу, делать запасы впрок. Так, люди научились считать, производить вычисления.
Для счёта сначала использовали пальцы на руках, если их не хватало, переходили на пальцы ног, применяли для счёта различные предметы (ракушки, палочки, камешки, узелки на веревках, зарубки на палках и т.д.), пока не были придуманы цифры и запись чисел.
Запись чисел придумали первыми шумеры. Для записи чисел использовалось всего две цифры: вертикальная черточка – одна единица, угол из двух черточек – 10.
Народ майя использовал вместо цифр рисунки-головы, которые было сложно отличить друг от друга.
Древние индийцы изобрели для каждой цифры свой знак, которые позволяли запоминать и записывать.
Римляне ввели десятичную систему счисления. Римские цифры до сих пор используют в часах и для оглавления книг, но такая система цифр тоже была слишком сложной для счета.
Предки русского народа – славяне – для обозначения чисел употребляли буквы (Приложение 1). Лишь Петр I ввел в России привычные для нас десять арабских цифр, которыми мы пользуемся до сих пор при вычислениях.
О феноменальных способностях людей быстро и правильно вычислять в уме известно давно. Многие учёные овладевают навыками и приёмами быстрого счета: Карл Гаусс, Андре Ампер. В настоящее время в России тоже живут люди, обладающие способностью быстро считать, например, артист Горный Ю.Г., Владимир Кутюков, А.В. Некрасов. Их называют «супер-счётчики».
Начиная с 2004 года, один раз в два года проводится Мировой чемпионат по вычислениям в уме, на который собираются лучшие из ныне живущих феноменальных счётчиков планеты. Соревнования проводятся по решению таких задач, как сложение десяти 10-значных чисел, умножение двух 8-значных чисел, расчёт заданной даты по календарю с 1600 по 2100 годы, корень квадратный из 6–значного числа. Также определяется победитель в категории «Лучший универсальный феноменальный счётчик» по итогам решения шести неизвестных «задач с сюрпризом».
В настоящее время в прибалтийских странах, Словении и Украине проводятся соревнования по устному счёту среди школьников под названием “Пранглимине”.
Разработчиками приёмов быстрого счета можно назвать таких ученых как Перельман Яков Сидорович (19 век), Берман Георгий Николаевич (20 век), Яков Трахтенберг (20 век) и многие другие.
Наиболее известен в информационных источниках метод Трахтенберга – система быстрого счёта, состоящая из набора легко запоминающихся шаблонов, которые позволяют любому быстро производить арифметические подсчёты. Самые важные алгоритмы в системе – алгоритмы для умножения, деления и сложения.
Результаты анкетирования «Приёмы быстрого счёта»
Перед тем, как обрабатывать информацию, собранную из информационных источников, я провела анкетирование. Моим одноклассникам было предложено ответить на вопросы анкеты «Приёмы быстрого счёта» (Приложение 2).
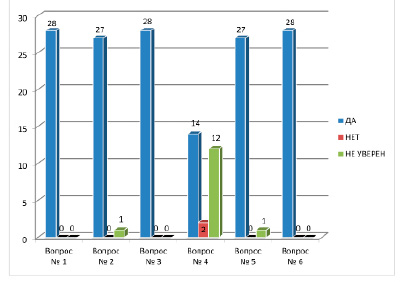
В анкетировании приняли участие 28 человек.
Проведя статистическую обработку данных, были получены следующие результаты:
1) умение считать подтвердили все 28 учащихся,
2) 27 из них уверены, что умение считать необходимо в жизни, 1 человек – не уверен
3) 28 из 28 человек подтвердили, что умеют складывать, умножать, вычитать и делить
4) приемы быстрого счета знают 14 учеников, 12 человек – не уверены в своих знаниях, 2 человека отметили, что приёмов быстрого счёта не знают
5) 27 учеников хотят узнать больше приёмов быстрого счёта, 1 человек – не уверен
6) все анкетируемые ученики уверены, что знание приёмов быстрого счёта пригодится в жизни (Приложение 3).
По результам анкетирования можно сделать вывод, что половина класса не владеют приёмами быстрого счёта, но хотят их узнать, потому что уверены, что это может пригодиться в жизни. В школьных учебниках очень редко встречаются объяснения приёмов быстрого счёта, поэтому для того, чтобы мои одноклассники смогли изучить и запомнить я решила создать буклет «Приёмы быстрого счёта» (для тех, кто хочет быстро считать в уме)» (Приложение 4).
Приёмы быстрого счёта
На уроках математики наблюдая за работающими у доски ребятами, я обратила внимание, что многие напрасно тратят времени и не всегда точно осуществляют вычисления даже в простых, на мой взгляд, примерах: умножение на 4, на 5, на 9, на 11, умножение двузначных чисел от 10 до 20 и от 20 до 30, вычитание из тысячи трехзначного числа и другие.
Легкими для запоминания и применимые на практике я считаю следующие приёмы быстрого счёта:
1. Умножение на 9
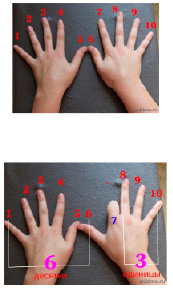
С приёмом я познакомилась при изучении таблицы умножения на 9. Чтобы умножить любое число от 1 до 9 на 9, нужно использовать пальцы рук. Необходимо загнуть палец, который соответствует умножаемому числу, например 9*7 (загните седьмой палец), сосчитать пальцы до загнутого пальца (в случае 9*7 – это 6), затем посчитайте после загнутого пальца (в нашем случае – 3). Ответ – 63 (Приложение 5).
2. Умножение на 11
Умножать на 11 немного сложнее, чем умножать на 10. Например,
36 • 11 = 396.
Складываем две цифры первого множителя: 3+6 = 9, помещаем результат между двумя цифрами первого множителя: 396.
Или, пример
57 • 11 = 627.
Складываем две цифры первого множителя: 5 + 7 = 12.
Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9:
5 + 1 = 6 (справа остается второй символ – двойка). На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 2, которую ставим в центр, и дописываем 7.
Ответ: 627.
3. Умножение на 5
Я очень легко запомнила таблицу умножения на 5. А вот когда на 5 нужно умножить большие числа, сделать это становится сложнее. Этот приём мне показался легким.
Возьмите любое число (я взяла чётное, так как десятичные дроби ещё не изучала), разделите на 2. В результате получилось целое число, припишите 0 в конце.
3458•5 =17290.
3458 : 2 = 1729 добавьте 0, получается 17290
4. Умножение на 4
Это очень простой прием,но не все сразу это могут заметить. Нужно просто умножить на 2, а затем опять умножить на 2:
57*4 = (57*2) + (57*2) = =(114) + (114) = 228.
5. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:
1000–648=?
9 – 6 = 3
9 – 4 = 5
10 – 8 = 2
Ответ: 352.
6. Умножение двузначных чисел от 10 до 20
Чтобы умножить два двузначных числа от 10 до 20, необходимо к первому числу прибавить цифру единиц второго числа, к результату, увеличенному в 10 раз прибавить произведение единиц данных чисел
16•17=(16+7)10+6•7= 23•10+42=230+42=272
7. Умножение чисел от 20 до 30
Чтобы умножить два двузначных числа от 20 до 30, необходимо к первому числу прибавить цифру единиц второго числа, к результату, увеличенному в 20 раз прибавить произведение единиц данных чисел
26•27=(26+7)20+6•7= =33•20+42=660+42=702.
8. Подсчет чаевых
Некоторые приёмы быстрого счёта можно применять не только на уроках математики. Например, гуляя с родителями по парку, мы зашли в кафе, заказали чай и яблочный штрудель. Затем папа попросил счёт. Официант принес чек, в котором написано, что к оплате 940 рублей. Папа сказал, что нужно еще чаевые оставить. А мама добавила, что принято оставлять от 7 до 15 процентов чаевых. Я решила подсчитать сумму чаевых. Вот что у меня получилось:
Если вам нужно оставить 15 % чаевых, есть простой способ сделать это.
Высчитайте 10 % (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ, например, в кафе необходимо заплатить 900 рублей.
900:10 =90 (руб.) – 10 % чаевых
90:2=45 (руб.) – 5 % чаевых
90+45=135 (руб.) – 15 % чаевых.
Существует очень много приёмов быстрого счёта. Мною были выбраны легкодоступные и быстро запоминающиеся.
Заключение
Каждый человека в жизни сталкивается с тем, что ему приходится выполнять достаточно сложные расчеты. Бытует мнение, что вычислять и считать должен компьютер, а человек должен отои?ти от этого занятия. Это мнение ошибочно, так как современные ученые обнаружили, что у нынешнего поколения происходит снижение умственных способностей. В то же время, учёные доказывают, что устные вычисления активизируют мыслительную деятельность.
Приёмы быстрого счёта, которые я рассматривала, не требуют уникальных способностей от человека. Но следует помнить, что счёт является простым и лёгким делом только тогда, когда владеешь особыми приёмами и навыками.
Цель научно-исследовательской работы “изучение и освоение некоторых приёмов быстрого счёта, которые могут применяться в учебной деятельности и в жизни» – достигнута.
В ходе подготовки и реализации результатов научно-исследовательской работы была найдена и изучена информация по теме «Приёмы быстрого счёта» освоено несколько приёмов быстрого счёта, которые могут быть применимы в учебной деятельности и в жизни создан буклет для одноклассников о приёмах быстрого счета (для тех, кто хочет быстро считать в уме).
Каждый может улучшить свои вычислительные навыки, используя приёмы быстрого счёта. Используя некоторые из этих приёмов на уроках или в жизненных ситуациях, можно развить скорость вычислений, добиться успехов в изучении всех школьных предметов, укрепить память, улучшить умение концентрироваться, внимание, наблюдательность. Знания приёмов быстрого счёта позволят школьникам упростить вычисления, сэкономить время.
Приложение 1
Запись чисел древними шумерами

Запись чисел древними индийцами

Запись римских чисел

Запись чисел Древней Руси

Приложение 2
Анкета «Приёмы быстрого счёта »
1. Умеете ли вы считать?
Да Нет Не уверен
2. Как ты думаешь, нужны ли умения считать в жизни?
Да Нет Не уверен
3. Умеешь ли ты складывать, умножать, вычитать, делить числа ?
Да Нет Не уверен
4. Знаешь ли ты приёмы быстрого счёта?
Да Нет Не уверен
5. Хотел(а) бы ты узнать больше приёмов быстрого счёта?
Да Нет Не уверен
6. Как ты думаешь, пригодятся ли тебе приёмы быстрого счёта в жизни?
Да Нет Не уверен
Приложение 3
Результаты анкетирования
|
Вопрос |
Ответ на вопрос |
||
|
ДА |
НЕТ |
НЕ УВЕРЕН |
|
|
Умеете ли вы считать? |
28 |
0 |
0 |
|
Как ты думаешь, нужны ли умения считать в жизни? |
27 |
0 |
1 |
|
Умеешь ли ты складывать, умножать, вычитать, делить числа ? |
28 |
0 |
0 |
|
Знаешь ли ты приёмы быстрого счёта? |
14 |
2 |
12 |
|
Хотел(а) бы ты узнать больше приёмов быстрого счёта? |
27 |
0 |
1 |
|
Как ты думаешь, пригодятся ли тебе приёмы быстрого счёта в жизни? |
28 |
0 |
0 |
Приложение 4
Приложение 5
Умножение на 9
Библиографическая ссылка
Кристианс Е.А. НЕКОТОРЫЕ ПРИЁМЫ БЫСТРОГО СЧЁТА В УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ И В ЖИЗНИ // Старт в науке. 2018. № 5-6. ;URL: https://science-start.ru/ru/article/view?id=1221 (дата обращения: 12.03.2026).
