• Авторы
• Научный руководитель
• Файлы
• Литература

Мартюшева А.Р. 1

---

1 г. Реутов, МАОУ «Лицей», 7 класс

Гришко Г.А. (Реутов, МАОУ «Лицей»)

Статья в формате PDF

12815 KB

1. Мандельброт Б. Фрактальная геометрия природы. – М.: Институт компьютерных исследований, 2002.

2. Кириллов А.А. Повесть о двух фракталах / МЦНМО, 2016.

3. Васильев А.Н. Самоучитель Си++ с примерами и задачами. – СПб.: Наука и Техника, 2010.

4. Крилли Т. Математика. 50 идей, о которых нужно знать. – М.: Фантом Пресс, 2015.

5. Треугольник Серпинского // Википедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Треугольник_Серпинского.

Всё, чему мы хотим научиться, мы учимся, делая.

Аристотель. Этика Никомахи II.

Фрактальная геометрия относительно новая научная дисциплина. С помощью фрактальной теории возможно точно описать многие «неправильные» формы встречающиеся в окружающем мире, например, береговую линию, форму облака и горного массива, ритм сердечных сокращений, ветвление сосудов в организме и речных дельт. Фрактальная геометрия помогает лучше понять многие явления с математической точки зрения.

Основная цель работы – это исследование геометрических фракталов, выявление общих закономерностей при построении и расчетах.

Гипотеза исследования – фракталы являются необычными геометрическими фигурами с особыми свойствами. С помощью фрактальной теории можно анализировать, решать различные, внешне не похожие друг на друга, задачи.

Для достижения поставленной цели решены следующие задачи: на конкретных примерах продемонстрированы особенности пошагового построения геометрических фракталов; самостоятельно выведены формулы (отличающиеся от стандартных) для расчета приращения периметра и площади фигур для каждого шага итерации; выявлены закономерности в расчетах и написаны программы на языке программирования «С++» для автоматизированного расчета периметра и площади фракталов на любом шаге итерации; описаны особенности и свойства отдельных фракталов.

Отличие данной работы от других, схожих по теме, в том, что для конкретных геометрических фракталов вывод формул идет от простого к сложному – многократное деление/умножение приводит к степеням и степенным выражениям, что обеспечивает наглядность и простоту восприятия; наглядно показано сопоставление изменений периметра и площади для n-шагов итерации.

Практическая значимость проекта: умение применять разнообразные методы, альтернативные способы решения задач; использование проекта, как дополнительного материала для интегрированных уроков по математике и информатике; совершенствование математической культуры, навыков математического мышления.

Все иллюстрации с построением фракталов выполнены автором.

Фрактал – геометрическая фигура, у которой каждый фрагмент повторяется при изменении (уменьшении) масштаба и любая часть фигуры похожа на всю фигуру в целом, т.е. вид фрактала не меняется в любом пространственном масштабе – бесконечно самоподобная фигура. Поэтому когда в работе говорим о расчетах периметра и площади фигуры, то подразумеваем периметр и площадь для каких-то конкретных шагов итерации – нельзя посчитать периметр и площадь всего фрактала. Чтобы увидеть всю красоту изменения периметра и площади необходимо провести расчеты не менее чем на 10–20 шагов, а для некоторых фракталов желательно до 50–100 шагов (например, ковер Серпинского). Но считать вручную, это довольно трудоемкий процесс. Поэтому с помощью выведенных формул расчеты были автоматизированы.

Общий порядок исследования фракталов:

1. Поэтапное построение геометрических (конструктивных) фракталов.

2. Расчет ручным способом периметра и площади фигур на каждом шаге итерации. Выявление закономерностей при расчете.

3. Создание программ на языке программирования «С++» для автоматизированного расчета периметра и площади фигур на каждом шаге итерации. Сопоставление периметра и площади для некоторых фракталов.

4. Выводы.

1. Квадратная звезда

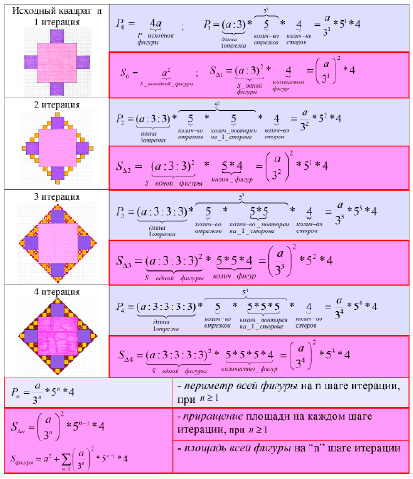
Строим геометрический фрактал «Квадратная звезда». Для наглядности результаты каждого шага построения раскрашиваем в свой определенный цвет. Для каждого шага итерации n в соответствии с рисунком выводим формулы расчета приращения периметра 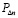и площади фигуры .

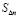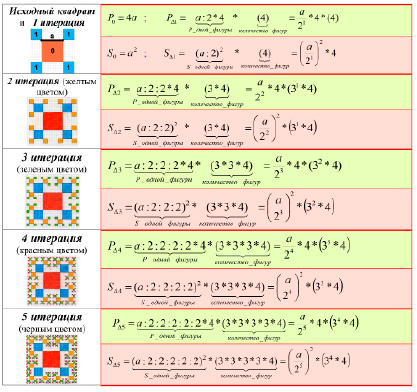
Из приведенных выше формул пошагового расчета периметра и площади видна закономерность: номер шага итерации n везде присутствует в формулах в виде степени. Если существует закономерность, то можно вывести обобщенные формулы для расчета приращения периметра и площади для каждого шага итерации и итоговые формулы P и S.

Для автоматизированного расчета периметра и площади фрактала «Квадратная звезда» на любом шаге итерации по выведенным формулам были написаны программы на языке программирования «С++». Результаты расчета программы выведены в таблицу (длина стороны исходной фигуры a = 10).

Как видно из расчетов, периметр резко увеличивается – за 20 шагов итерации примерно в 13.300 раз, а площадь растет очень медленно – всего в 5 раз. Примерно с 17 шага площадь практически перестает увеличиваться. А периметр «бешено» растет! Получается, что для данного фрактала периметр и площадь практически не зависят друг от друга – каждый меняется со своей «скоростью». Первые 5–6 шагов итерации отражены на отдельных диаграммах. На первых шагах пока еще видна в масштабе пошаговая разница. При иллюстрации более «дальних» шагов изменения в площади не будут видны совсем из-за их незначительных величин по сравнению с изменениями P.

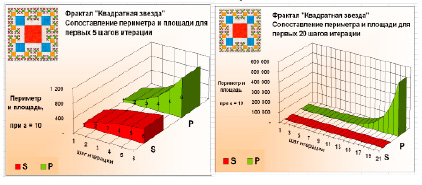
Еще стоит отметить, что на протяжении этих 20 шагов изменения площади относительно периметра происходило очень непропорционально. С каждым шагом итерации происходит резкое приращение периметра, а приращение площади стремится к нулю. И чем больше шаг итерации, тем огромнее разница в приращениях.

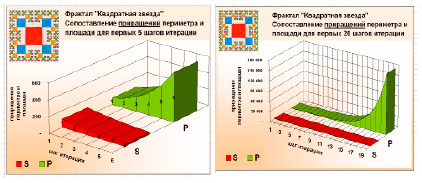
2. Квадратная звезда с пересечением

Строим геометрический фрактал «Квадратная звезда с пересечением» и для каждого шага итерации n в соответствии с рисунком выводим формулы расчета приращения периметра 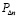и площади фигуры .

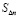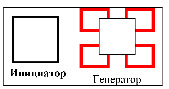
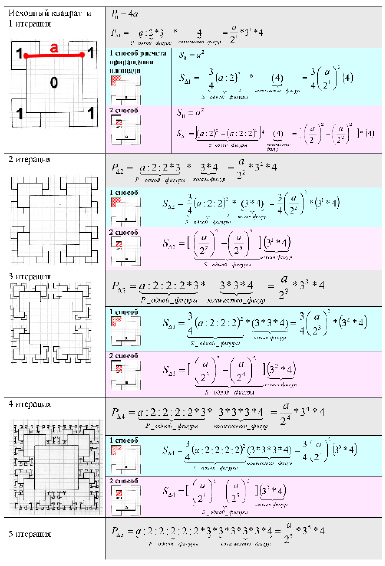
Для автоматизированного расчета периметра и площади фрактала «Квадратная звезда с пересечением» на любом шаге итерации написана программа на языке «С++». Результаты расчета программы выведены в таблицу (длина стороны исходной фигуры a = 10).

Как видно из таблицы, результаты расчетов периметра и площади фрактала «Квадратная звезда с пересечением» аналогичны результатам расчета вышеописанного фрактала «Квадратная звезда»:

– периметр фрактала резко увеличивается – за первые 20 шагов итерации примерно в 10.000 раз, а площадь растет очень медленно – всего в 4 раза;

– примерно с 17 шага итерации площадь практически перестает изменяться, а периметр сильно (!) растет. Для данного фрактала периметр и площадь мало зависят друг от друга.

Наглядно увидеть изменения можно на диаграммах.

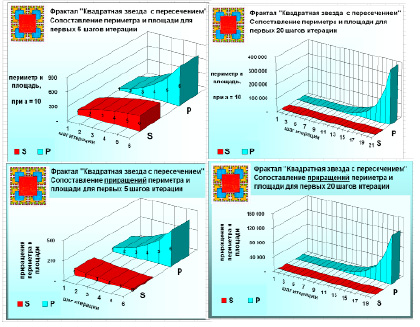
Из графиков видно, что с каждым шагом итерации происходит резкое приращение периметра, а приращение площади стремится к нулю. И чем больше шаг итерации, тем огромнее разница в приращениях.

По характеру изменения периметра и площади фракталы «Квадратная звезда» и «Квадратная Звезда с пересечением» аналогичны.

4. Ковёр Серпинского

Строим геометрический фрактал «Ковер Серпинского». В квадрате каждую из сторон делим на три равные части. Соответственно весь квадрат поделится на девять одинаковых квадратиков со стороной равной 1/3 от исходной длины. Из исходной фигуры вырезаем центральный квадрат. Затем такой же процедуре деления и вырезания подвергается каждый из 8 оставшихся квадратиков и далее процесс повторяется.

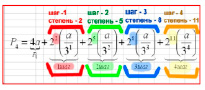
При построении для каждого шага итерации n в соответствии с рисунком выводим формулы расчета периметра Pn и площади Sn.

Для вывода общих формул потребовались дополнительные расчеты, приведенные ниже.

Дополнительные расчеты

1. Установление соответствия между номером шага итерации и показателем степени при расчете периметра фрактала «Ковер Серпинского».

Из данной формулы видно, что между номером шага и показателем степени существует зависимость.

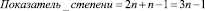
Проверим пошагово результаты расчетов по этой формуле (данные в таблице).

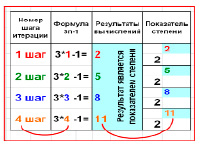
Вывод: Между номером шага итерации и показателем степени существует зависимость

Показатель_степени=3n–1 

Эту формулу мы будем использовать при расчете периметра всей фигуры на n шаге итерации.

2. Установление соответствия между номером шага итерации и показателем степени при расчете площади фрактала «Ковер Серпинского».

Из данной формулы видно, что между номером шага и показателем степени существует зависимость:

Показатель_степени=3n–3 

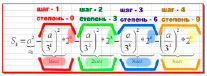
Проверим пошагово результаты расчетов по этой формуле (данные в таблице).

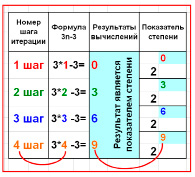
Вывод: Между номером шага итерации и показателем степени существует зависимость

Показатель_степени=3n–3 

Эту формулу мы будем использовать при расчете площади всей фигуры на n шаге итерации.

Для автоматизированного расчета периметра и площади фрактала «Ковер Серпинского» на любом шаге итерации написана программа на языке «С++». Результаты расчета программы сведены в таблицу (длина стороны исходной фигуры a = 10):

Окончание табл.

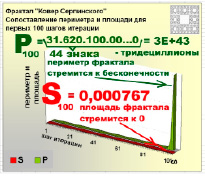
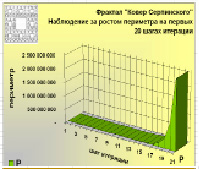
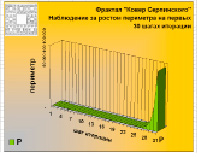
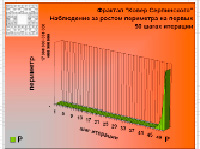
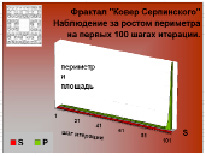
Как видно из расчетов, особенно после 80х шагов итерации, площадь такого ковра практически равна нулю, а общий периметр всех пустот становится огромным и стремится к бесконечности.

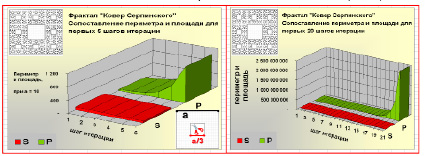
На диаграммах наглядно показано, как взаимно изменяются периметр и площадь фрактала на каждом шаге итерации. На первых 5–6 шагах, хотя и еле заметна, но пока еще видна пошаговая разница в масштабе. При иллюстрации в масштабе более «дальних» шагов изменения площади не будут видны совсем из-за их незначительных величин по сравнению с изменениями периметра.

В процессе построения у фрактала «Ковер Серпинского» образуются пустоты. Это «дырявая» фигура. Учитывая такую особенность и принцип «выбрасывания» частей квадрата на каждом шаге итерации, приходим к тому, что «площадь такого ковра обращается в нуль, а общий периметр его пустот стремится к бесконечности» [1]. Такое свойство ковра подтверждается расчетами и наглядно проиллюстрировано на диаграммах – площадь «дырявой» фигуры стремится к нулю, а периметр скачкообразно «выстреливает» вверх на последних шагах итерации. В этом треугольник Серпинского и ковер Серпинского аналогичны.

Если сравнивать наглядные изображения треугольника и ковра, то можно увидеть принципиальное различие между фракталами: в треугольнике все пустоты пересекаются (касаются) друг с другом в точках и расползаются дальше, а ковровые пустоты не имеют между собой ничего общего – каждая пустота «самостоятельна» и не соприкасается с другой.

5. Снежинка Коха

Строим геометрический фрактал «Снежинку Коха» и для каждого шага итерации n в соответствии с рисунком выводим формулу расчета итогового периметра .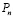

Для автоматизированного расчета периметра фрактала «Снежинка Коха» на любом шаге итерации написана программа на языке «С++». В таблице результаты расчетов.

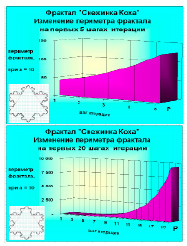
Как видно из расчетов, за первые 20 шагов итерации, периметр увеличился – примерно в 240 раз. По сравнению с другими фракталами, периметр снежинки Коха растет довольно медленно. Это видно и из диаграммы – можно наблюдать, не только последние 3–4 шага, а увидеть изменения периметра на протяжении последних 10–12 шагов. Площадь фрактала активно увеличивается на 1–2 шаге итерации, далее рост существенно замедляется с каждым шагом.

6. Снежинка Коха квадратная

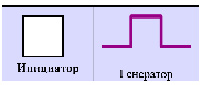
Создадим новый фрактал: будем строить кривую Коха на сторонах квадрата – альтернативную снежинку Коха. Для каждого шага итерации n в соответствии с рисунком выводим формулы расчета периметра 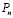и приращения площади фигуры .

Для автоматизированного расчета периметра и площади фрактала «Снежинка Коха квадратная» на любом шаге итерации написана программа на языке «С++». Результаты расчета программы выведены в таблицу и наглядно представлены на диаграммах.

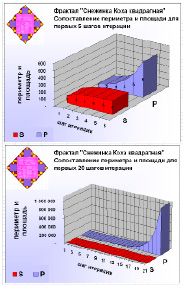
Как видно по результатам расчетов:

– периметр фрактала резко увеличивается – за первые 20 шагов итерации примерно в 27.000 раз, а площадь растет очень медленно – всего в 2 раза;

– примерно с 8 шага итерации площадь практически перестает изменяться, а периметр сильно (!) растет. Для данного фрактала периметр и площадь мало зависят друг от друга.

Анализ результатов работы

В процессе построения конкретных фракталов и изучения их особенностей были выявлены следующие закономерности и свойства:

1. Для всех исследованных фигур в формулах расчета периметра и площади существует закономерность: номер шага итерации n везде присутствует в формулах в виде степени.

2. Изменения площади более существенны и заметны только на первых шагах итерации, после первых шагов площадь почти перестает изменяться.

3. Увеличение периметра идет очень (!) быстро с каждым шагом. Поэтому на графиках виден «всплеск» изменения периметра только на последних шагах итерации (см.диаграммы). Все предыдущие изменения периметра по сравнению с последними шагами являются ничтожными. И это характерно на всем протяжении «роста» фракталов. Сколько бы ни было предыдущих шагов итерации, на графиках видны скачки только последних шагов.

4. Изменения площади практически не зависят от изменений периметра и происходят очень непропорционально относительно друг друга. С каждым шагом итерации идет резкое приращение периметра, а приращение площади стремится к нулю. И чем больше шаг итерации, тем огромнее разница в приращениях.

5. Длина «истинного фрактала» всегда стремится к бесконечности

6. Графики изменения периметра и площади практически однотипны для всех фракталов.

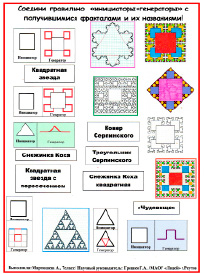
Наглядный материал для проведения интегрированных уроков (математика, информатика) среди учащихся .

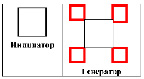
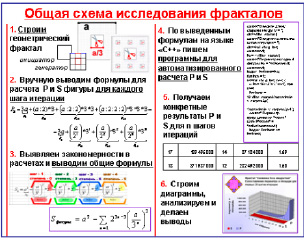
Головоломка «Соедини правильно «инициаторы+генераторы» с получившимися фракталами и их названиями!»

Библиографическая ссылка