• Авторы
• Научный руководитель
• Файлы
• Литература

Ковалева Е.А 1

---

1 г. Липецк, МАОУ СШ №59 «Перспектива», 8 класс

Меньщикова Т.В. (Липецк, ЛГТУ)

Хабибуллина Е.Л. (Липецк, МАОУ СОШ 59)

Статья в формате PDF

0 KB

1. Кудинов Ю.И. Интеллектуальные системы [Электронный ресурс] : учебное пособие / Ю.И. Кудинов. – Электрон. текстовые данные. – Липецк: Липецкий государственный технический университет, ЭБС АСВ, 2014. – 63 c. – 978-5-88247-653-2. – Режим доступа: http://www.iprbookshop.ru/55089.html

2. Еременко Ю. И. Интеллектуальные системы принятия решений и управления : учебное пособие для вузов / Ю. И. Еременко. – Старый Оскол: ТНТ, 2015.

3. Аверченков В.И. Эволюционное моделирование и его применение [Электронный ресурс] : монография / В.И. Аверченков, П.В. Казаков. – Электрон. текстовые данные. – Брянск: Брянский государственный технический университет, 2012. – 200 c. – 5-89838-441-X. – Режим доступа: http://www.iprbookshop.ru/7012.html

4. Электронный ресурс «Генетический алгоритм. Просто о сложном» https://habrahabr.ru/post/128704/

5. И. Ф. Астахова, А. М. Фирас Составление расписания учебных занятий на основе генетического алгоритма URL:http://www.vestnik.vsu.ru/pdf/analiz/2013/02/2013-02-17.pdf.

Каждый учебный год заместители директоров школ тратят недели на составление расписания. Казалось бы, что может быть проще, чем просто распределить предметы по дням недели. Но все на самом деле все гораздо сложнее.

В нашей школе много учителей работают по совместительству, и им важно, чтобы график работы в школе не пересекался с графиком по основному месту работы. Помимо пожеланий учителей существуют санитарные нормы и правила организации учебного процесса, которые необходимо соблюдать.

Постановка задачи

Одной из важнейших и актуальных задач, решаемых системой управления образовательным учреждением, является составление расписания занятий. При этом формирование расписания учебных занятий для многих школ проблемно, поскольку требует значительных затрат времени и материальных ресурсов.

Цель моего исследование: изучение применимости генетического алгоритма к задаче о составлении расписания.

При составлении расписания необходимо в первую очередь руководствоваться требованиями СанПиН и пожеланиями учителей, так как это является критериями качества составленного расписания. Работоспособность учащихся в разные дни учебной недели отличается. Ее уровень растет к середине недели и остается низким в понедельник и в пятницу. Распределение учебной нагрузки в течение недели строится так, чтобы наибольший объем приходится на вторник и четверг. В эти дни в расписание уроков включаются либо наиболее трудные предметы, либо средние и легкие, но в большем количестве. В 10-12 часов происходит наиболее эффективное усвоение материала без больших психофизических затрат организма.

В таблице 1 приведена шкала трудности учебных предметов для учеников восьмых классов по 13-балльной шкале М.И. Степановой, И.Э. Александровой, А.С. Седовой [3], а также – количество часов в неделю.

Таблица 1

Шкала трудности учебных предметов, изучаемых в восьмом классе

Суммарная трудоемкость в неделю: 231 единица

Совместно с руководством школы была составлена таблица допустимых значений трудности учебных дней, для учеников восьмых классов.

Таблица 2

Таблица допустимых значений трудности учебных дней

Также необходимо чередовать предметы различных предметных областей, так как для повышения работоспособности учащихся необходима смена деятельности. В таблице 3 приведены предметные области и учебные предметы, которые в них входят.

Таблица 3

Предметные области и учебные предметы, которые в них входят

В таблице 4 приведено желаемое место предметов в расписании, согласно нормам СанПин.

Таблица 4

Желаемое место предметов в расписании, согласно нормам СанПин

Кроме норм СанПин необходимо также учитывать интересы педагогов.

Генетический алгоритм

Генетический алгоритм – алгоритм, основанный на природных процессах (использующий эволюционные принципы). Эвристические алгоритмы помогают найти «достаточно хорошее» решение, а не оптимальное, что и требуется при решении задачи составления расписания.

3.1 Описание структуры особи

Исходной информацией для составления расписания уроков являются следующие множества:

D- учебные предметы;

K- классы;

P- учителя;

T- временные интервалы проведения уроков.

Все они связанны между собой и представляют единый учебный процесс. Теоретико-множественной моделью расписания является функция, отображающая их декартово произведение 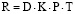на множество {0;1}:

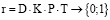
Запись 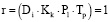означает, что предмет Di у класса Kk проводится во время урока Tp учителем Pl. То есть 1 обозначает, что данный вариант включен в расписание, а 0 показывает, что данный вариант в него не входит.

Группы объектов «учителя», «учебные предметы», «классы» являются основными, потому что они определяют какие учебные предметы, в каком классе и каким учителем будут проводиться. Так как эти множества тесно связаны между собой, их можно объединить в один блок «занятие». В задаче составления расписания таких блоков используется несколько.

Объединим все блоки во множество уроков. Оно состоит из 99 элементов (33 урока в каждом из трех классов).

Закодируем значения генов «занятие» следующим образом. Элементы для 8А класса будут записаны в формате 1** (**- номер варианта из 33). Элементы для 8Б класса будут записаны в формате 2** (**- номер варианта из 33). Элементы для 8В класса будут записаны в формате 3** (**- номер варианта из 33). Полный список элементов множества приведен в приложении 1.

3.2 Описание генетического алгоритма в задаче о составлении расписания

При решении задачи составления расписания особью будет являться возможный вариант расписания уроков. Она состоит из 3 хромосом. А хромосомой является один класс. Хромосома состоит из генов – блоков «занятие».

По нормам СанПин в понедельник и пятницу должно быть 6 уроков, а всего уроков в неделю должно быть 33. Поэтому на вторник, среду и четверг приходится 21, то есть на каждый из этих дней по 7 уроков (21/3=7).

Применение генетического алгоритма в задаче составления расписания

В генетическом алгоритме выделяют следующие шаги: формирование начальной популяции, оценивание популяции, селекция, скрещивание, мутация.

1. Формирование начальной популяции

В большинстве случаев начальная популяция формируется случайным образом. В случае если она окажется не конкурентоспособной, алгоритм с большой вероятностью исправит это. Поэтому на первом этапе не обязательно делать очень приспособленных особей, достаточно того, чтобы они соответствовали «формату» особей и могли «размножаться».

2. Оценивание популяции

Оценивание популяции помогает выявить наиболее приспособленных и наименее приспособленных особей. Для этого используется функция качества 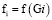. Как правило, данный алгоритм используется для решения задач минимизации и максимизации функции, в первом случае необходимо найти минимальное значение функции, а во втором максимальное.

В ходе работы были выделены критерии качества: трудоемкость учебного дня, чередование предметов различных предметных областей, место предметов в расписании и пожелания учителей. За их нарушение будет увеличиваться значение функции качества. Так как при составлении расписания в первую очередь необходимо учитывать нормы СанПин, а пожелания учителей являются наименее важным критерием, то каждому ограничению был присвоен коэффициент, на который будет умножаться число нарушений. Таким образом, функция качества (для данного алгоритма) принимает следующий вид:

,

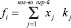где xj = {0;1;2} – признак нарушения, который показывает наличие нарушения и его степень;

kj – коэффициент значимости критерия.

Так как каждый критерий качества имеет свой коэффициент значимости, упорядочим их в порядке убывания.

а) Трудоемкость учебного дня.

На первом шаге вычисляем трудоемкость каждого дня. Если она превышает допустимую, то xj =1, если нет, то xj =0. Коэффициент, на который будет умножаться значение k =4.

б) Чередование предметов разных предметных областей.

Вычисляется количество чередований для каждого дня. Для этого необходимо сравнить два стоящих рядом предмета в расписании на один учебный день, если они относятся к разным предметным областям, то увеличиваем число чередований. Значение xj зависит от их числа. Возможные значения xj приведены в таблице 5.

Таблица 5

Возможные значения xj

Коэффициент, на который будет умножаться значение k =3.

в) Место предметов в расписании.

Сравнивается положение предмета в варианте расписания с требованиями СанПин. Если оно им соответствует, то xj = 0, если нет, то xj = 1. Коэффициент, на который будет умножаться значение k = 2.

г) Пожелания учителей.

Проверяем соответствие пожеланиям учителей положение блока занятие в расписании. Если оно им соответствует, то xj = 0, если нет, то xj = 1. Коэффициент, на который будет умножаться значение k =1.

3. Селекция

При помощи селекции выбираются наиболее приспособленные особи для скрещивания. Это происходит при помощи одного из видов селекции:

а) рулеточная селекция

В данном виде селекции процесс отбора особей можно сравнить с игрой в «рулетку». Круг делится на сектора, количество которых равно количеству особей. Каждый сектор пропорционален значению функции приспособленности. Далее n раз вращается рулетка (n-размер популяции). Особь, выбранная для скрещивания, выбирается по сектору, на котором остановилась рулетка.

б) селекция усечением

Сначала вычисляется приспособленность каждой особи. Далее отбирается l•n лучших особей (l-порог отсечения; n-размер популяции). Главное преимущество этого способа заключается в том, что шансы на выживание у плохо приспособленных особей малы.

в) турнирный отбор

Сначала популяция делится на подгруппы. Обычно каждая подгруппа состоит из 2-5 особей. В результате «турниров» в каждой подгруппе отбираются наиболее приспособленные особи.

В таблице 6 представлено сравнение способов селекции.

Таблица 6

Преимущества методов

По составленной таблице, можно сделать вывод, что наиболее подходящим методом для решения задачи о составлении расписания является метод турнирного отбора, так как основным критерием выбора метода является эффективность метода для поставленной задачи, а метод турнирного отбора позволяет избежать «застревания» в области локального максимума, не являющегося глобальным максимумом (по значению функции приспособленности).

4. Скрещивание

Особи, отобранные в результате селекции, называются родительским и будут принимать участие в скрещивании и давать потомство. Новое поколение формируется из особей, которые получились в результате обмена генетической информацией между родительскими особями. Для решения задачи о рюкзаке используется целочисленное кодирование, для которого часто используются следующие виды кроссовера:

а) одноточечный кроссовер

На начальном этапе выбирается произвольная точка разрыва. Далее происходит обмен частями хромосом.

б) двухточечный кроссовер

В начале, выбирается две произвольные точки разрыва. Далее родительские особи обмениваются частями, которые лежат между этими точками.

В результате скрещивания образуется новое поколение, которое может состоять не только из потомков, но и «элитные особи».

Обычно, по принципу Парето, доля потомков в новой популяции составляет 20%, остальные 80% – особи с наибольшим значением функции приспособленности (является обратной к функции штрафа).

5. Мутация

Оператор мутации вносит случайные изменения в хромосомы особей. Данная операция помогает эффективнее изучать пространство поиска.

При решении задачи составления расписания используется целочисленное кодирование, поэтому будем применять оператор битовой мутации. Оператор изменяет отдельные гены хромосомы с вероятностью VM. Так как эта операция повторяется D раз (D-количество разрядов хромосомы), значение VM выбирается небольшим, чтобы не разрушить «хорошие» хромосомы. Часто VM =D-1.

Рассмотренные операции повторяются до тех пор, пока изменение значения функции приспособленности не станет меньше заданного значения, или количество смененных поколений не будет равно заданному числу.

На рисунке 1 приведено сравнение эффективности изученных методов.

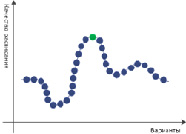
(а) График поиска решения переборными методами

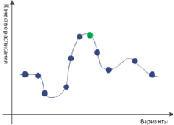
(б) График поиска решения эвристическими методами (генетический алгоритм)

Рисунок 1. Анализ эффективности методов

Заключение

В рамках исследовательской работы были изучены требования к составлению расписания; была изучена применимость генетического алгоритма к задаче составления расписания; генетический алгоритм был адаптирован к решению задачи о расписании, что позволит администрации школы с меньшими временными и вычислительными затратами (по сравнению с переборными методами) составлять расписание на новый учебный год.

Библиографическая ссылка