• Авторы
• Научный руководитель
• Файлы
• Литература

Цабадзе А.Д. 1

---

1 с. Видяево, МБОУ СОШ ЗАТО Видяево, 7 а класс

Шалованова Р.Н. (с. Видяево, МБОУ СОШ ЗАТО Видяево)

Статья в формате PDF

0 KB

1. Балк М.Б., Балк Г.Д. Математика после уроков. – М.: Просвещение, 1971. – 462 с.

2. Гарднер М. Математические чудеса и тайны. – М.: Наука, 1986. – 128 с.

3. Игнатьев Е.И. В царстве смекалки. – М.: Наука, 1978. – 192 с.

4. Коба В.И., Хмура О.О. Внеклассная работа по математике в школе, – Киев: Радянська школа, 1968. – 376 с.

5. Кордемский Б.А. Математическая смекалка. – М.: ООО «Издательство Оникс», 2005. – 576 с.

6. Ожегов С.И., Шведова Н.Ю. Толковый словарь русского языка. – М.: АЗЪ, 1996,-928 с.

7. Скобелев Г.М., Берман В.П. Математика после уроков. – Киев: Радянська школа, 1973. – 160 с.

8. Трошин В.В. Магия чисел и фигур. – М.: Глобус, 2007. – 382 с.

9. http://goodmagic.ru/tsiklicheskoe-chislo

«Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным»

Б. Паскаль

В настоящее время никто не станет отрицать необходимости популяризации математических знаний. Одним из способов популяризации являются математические фокусы, которые редко рассматриваются и применяются в обучении математики.

Математические фокусы – это эксперименты, основанные на математике, на свойствах фигур и чисел, и лишь обличенные в экстравагантную форму. И понять суть того или иного эксперимента – это значит понять пусть небольшую, но математическую закономерность. Для демонстрации этих фокусов не требуется специального оборудования и сложной подготовки.

Мартин Гарднер дал следующую классификацию математических фокусов: фокусы с картами, с мелкими предметами, со специальным снаряжением, топологические головоломки, исчезновение фигур, головоломки с числами. Он разбил головоломки с числами на три категории:

1) основанные на быстром счете;

2) с предсказанием результатов действий;

3) с отгадыванием чисел.

Проблема, подлежащая исследованию. Существует классификация фокусов с числами, которая не отражает закономерностей их разгадки и создания.

Гипотеза. В фокусах с числами можно выявить закономерности их разгадывания и составления.

Цель работы: выявление основных математических закономерностей разгадки и создания фокусов с числами.

Задачи:

- провести теоретический анализ различных источников о фокусах с числами (интернет, литература);

- выявить закономерности разгадки и создания фокусов с числами;

- придумать фокусы с числами на основе выявленных закономерностей;

- провести анкетирование по изучению заинтересованности учащихся класса математикой до и после демонстрации фокусов и способов их разгадывания и составления.

Объект исследования: математические фокусы.

Предмет исследования: закономерности в фокусах с числами.

Методы: поисково-исследовательский, наблюдение, анализ.

Методы проведения исследования:

1) изучение литературы, интернет источников о фокусах с числами;

2) анализ, классификация закономерностей разгадки и создания фокусов с числами;

3) использование полученной классификации для создания фокусов.

Новизна

Новизна данного исследования заключается в следующем:

- выявление основных математических закономерностей разгадки и создания фокусов с числами;

- математические фокусы редко рассматриваются и применяются в обучении математики. Данное исследование призвано привлечь внимание учащихся к изучению математики.

Практическая значимость

Полученные данные могут быть использованы:

- на уроках математики для развития памяти, устного счета, сообразительности, способности мыслить логически;

- на занятиях кружка, факультативных, элективных курсов по математике;

- на математических вечерах.

План выполнения исследования

1. Найти (в литературе, интернет источниках) и изучить классификацию фокусов с числами.

2. Выявить математические закономерности при разгадывании и создании фокусов с числами.

3. Придумать фокусы на основе полученных данных.

4. Оформить материалы исследования.

Математические закономерности в фокусах с числами

По словарю С.И. Ожегова «Фокус – это искусный трюк, основанный на обмане зрения, внимания при помощи ловкого и быстрого приема, движения» [6, с. 843]. Но фокусы с числами построены на математических закономерностях, скрытых от зрителя, не требуют дополнительного оборудования.

Первое упоминание о математических фокусах мы встречаем в книге русского математика Леонтия Филипповича Магницкого, опубликованной в 1703 году. Одна глава книги содержала математические игры и фокусы. Магницкий пишет, что поместил эту главу в книгу для «утехи и, особенно, для изощрения ума учащихся».

Математические фокусы интересны именно тем, что каждый фокус основан на математических законах. Смысл их состоит в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними. Главное – это то, что фокусник знает секрет: особые свойства чисел.

Проанализировав различные фокусы с числами, я выявила следующие закономерности их создания:

1) значение постоянной при счете по кругу (часах) в прямом и обратном направлениях от указанного числа;

2) свойства четности, нечетности чисел;

3) степени числа 2 или двоичная система счисления;

4) свойство последней цифры заданной системы счисления;

5) алгоритмы вычислений, приводящих к заранее известному результату;

6) софизмы.

Использование постоянной при счете по кругу (часах) в прямом и обратном направлениях от указанного числа

Пример. Пусть кто-нибудь задумал на круге 5, а вы указываете, например, 9, прибавляете про себя к нему 12, получите 21. Затем предлагаете зрителю считать про себя от задуманного им числа включительно (5) до 21, дотрагиваясь сначала к 9, потом к 8, потом к 7 и т. д., идя по кругу в обратном порядке. Когда он досчитает до 21, то сказать это число громко и остановиться. [3, с. 91].

Объяснение. От 5 до 9 включительно 5 чисел, прибавляем 12, получим 17 чисел. В обратном порядке от 9 до 5 включительно 5 чисел, прибавляем 12, получим 17 чисел.

Использование четности, нечетности чисел

Для разгадки некоторых фокусов используются свойства четности, нечетности чисел.

Пример. Отгадывание, в какой руке монета.

Зрителю 1 предлагается две монеты достоинством 10 копеек и 5 копеек, которые он прячет по одной в каждой руке. Фокусник предлагает зрителю умножить числовое значение монеты в правой руке на 4 (можно на любое четное число), а числовое значение монеты в левой руке умножить на 7 (можно на любое нечетное число), полученные результаты сложить и сказать, четное или нечетное число получилось в результате [7, с. 126].

Объяснение. При умножении на четное число получится четное, сумма четных чисел – четное число, нечетного и четного чисел – нечетное. Если в правой руке 10 копеек, то получим: 104 + 57 = 75, нечетное число. Если в правой руке 5 копеек, то получим: 54 + 107 = 90, четное число. Таким образом, если у зрителя получилось четное число, то в правой руке 5 копеек, а если нечетное, то 10 копеек.

Степени числа 2 или использование двоичной системы счисления

Пример. Отгадывание количества взятых предметов.

Зрителю предлагается из предметов, например, карандашей, лежащих на столе, взять любое количество. Отвернувшись, фокусник предлагает зрителю разделить количество предметов на две равные части. Если число предметов нечетно, то лишний предмет положить на первый левый из расположенных в ряд кружков. Если, число предметов четно, то кружочек оставить пустым. Одну половину предметов убирают совсем, а оставшуюся половину снова делят на две равные части, если останется лишний предмет, то положить его на второй кружок, если не останется, то оставить кружок пустым. Этот процесс продолжают до тех пор, пока не останется один предмет, который кладут на соответствующий кружок. После этого фокусник, повернувшись и посмотрев на кружки, называет количество предметов, которое было в начале игры [5, с. 25].

Объяснение. Фокусник складывает степени числа два, которые соответствуют кружкам, на которых лежат предметы. Например, для расположения 11001 (в двоичной системе счисления) соответствует 1 + 2 + 16 = 19.

Последняя цифра выбранной системы счисления

Пример. Отгадывание результата.

Зрителю предлагается записать любое трехзначное число, в котором первая и последняя цифры различны, и число, записанное в обратном порядке. Из большего числа нужно вычесть меньшее. Попросив зрителя назвать первую или последнюю цифру полученного числа, вы называете результат. Если теперь написать разность в обратном порядке и эти два числа сложить, то получится 1089 [2, с. 105].

Объяснение. В десятичной системе счисления последняя цифра 9. В разности получим число, в середине которого стоит 9, а сумма первой и последней цифр равна 9.

Использование алгоритмов вычислений, приводящих к заранее известному результату

К этой категории относятся многочисленные фокусы с календарями, квадратами, циклическим числом, угадывания числа как задуманного зрителем. так и заранее заклеенной фокусником в конверт записки с числом [9]. К каждому фокусу из этой категории существует свой алгоритм получения результата,

Пример 1. Угадывание задуманного числа.

Задумайте число, отнимите 1, полученную разность удвойте и прибавьте первоначально задуманное число. Скажите результат, я угадаю число [5, с.219].

Объяснение. Пусть задуманное число х. Тогда 2(х-1) + х = Зх-2. Значит, к названному числу надо прибавить 2, а потом разделить на З.

Пример 2. Числа Фибоначчи – элементы числовой последовательности, в которой каждое последующее число равно сумме двух предыдущих чисел. Ведущий предлагает записать цифры в столбик: меньшую вверху, а большую внизу. Далее необходимо записать результат сложение этих чисел ниже (под ними). Далее складываются два последних числа (второе и третье числа), а результат записывается ниже. И так далее пока не будет записано 10 чисел. Далее записи показываются ведущему, а он тут же пишет результат сложения этих 10 чисел.

Объяснение. Пусть задуманы числа а1 и а2. Тогда а1 + а2 + а3 + а4 + а5 + а6 + а7 + а8 + а9 + а10 = 55а1 + 88а2 = 11(5а1 + 8а2) = 11а7. Другими словами, чтобы быстро узнать сумму, нужно найти седьмое число и умножить его на 11.

Софизмы

Софизм – это рассуждение, в котором явно неправильный результат доказывается благодаря использованию доводов, ошибочность которых замаскирована [1, с. 151].

Пример. 2 = 3.

Зрителю предлагается в каждой части записи равенства 2-2 = 3-3 вынести общий множитель: 2(1-1) = 3(1-1). Выражения, стоящие в скобках, получились равные, сократим, получим 2 = 3. В чем ошибка?

Объяснение. 1-1 = 0, делить на нуль нельзя.

Придуманные фокусы

1. Фокус с часами. Задумайте какой-нибудь час (от 1 до 12). Задуманный вами час запомните. Теперь я буду указкой постукивать по часам, а вы считайте про себя от задуманного числа включительно, каждый раз, когда постучу, прибавляйте к задуманному вами числу по одному. Когда вы досчитаете до двадцати, остановите меня. Ведущий называет задуманное число.

2. Кто что выбрал. Я предлагаю своим подругам Веронике и Кате две карточки с числами, например, 12 и 7. Отвернувшись, предлагаю им распределить их между собой и выполнить, следующие действия: Вероника должна умножить свое число на 5, а Катя на 2. Затем они должны сложить полученные результаты и сказать мне, четное или нечетное число получилось. Я объявляю, кто какое число выбрал.

Ответ: если в результате четное число, число 12 выбрала Вероника, а если нечетное, то Катя.

3. Угадывание задуманного числа. Отгадывание числа из таблицы. Зрителю предлагается задумать любое число из предложенной таблицы (табл. 1) и назвать номера столбиков, в которых оно находится. После этого ведущий называет задуманное число.

Таблица 1

Отгадывание числа из таблицы

Объяснение. Каждое из чисел от 1 до 31 переведено в двоичную запись и расставлено в таблице в соответствии с этим кодом. Например, 27 = 16 + 8 + 2 + 1 = 24 + 23 + 21 + 20 = (11011)2. Эта запись означает, что число 27 нужно поставить в 1, 2, 4, 5 столбики. Чтобы назвать задуманное число, надо сложить числа первых рядов названных столбиков.

4. Волшебная девятка. Предлагается зрителю умножить на 9 любую цифру, кроме единицы. Пусть произнесет вслух только одну из двух цифр получившегося числа. Только обязательно уточнить, это первая или вторая цифра. Зрителю озвучивается все число целиком.

Объяснение. Если умножить любую цифру на 9, в результате получится двузначное число. Если сложить между собой обе цифры этого числа, получится 9. Например: 5 х 9 = 45. Пусть зритель назвал только «5». Зная, что сумма равна 9, нужно 9 – 5 = 4. Уточнить, первую или вторую цифру он называл. В зависимости от этого число будет либо 54, либо 45.

5. Гениальная память. Зрителю предлагается назвать любое двузначное число из таблицы (табл. 2), фокусник, не глядя на нее, называет число, стоящее под ним.

Объяснение. Пусть названо число 23, прибавляем 11, получим 34. Переставляем местами цифры, получим 43. Сложим цифры числа, получим 7. Это третья цифра числа. Сложим последние две цифры, получим 10, убираем десятки, четвертая цифра 0. Сложим третью и четвертую цифры, получим 7. Это пятая цифра. Процесс повторяется до получения седьмой цифры.

Телепат. Написать на бумаге цифры 1, 2, 3, 4, 5, 6, 7, 8, 9. Попросить кого-нибудь из зрителей выбрать три цифры, идущие подряд (это обязательное условие) и назвать их сумму. Сказать, какие цифры задумал зритель.

Объяснение. Сумму разделить в уме на 3. Это и будет средняя цифра. Назвать остальные не составит труда.

Например. Зритель назвал сумму 27. Делим 27 на 3 и получаем 9. Значит, загаданы были 8, 9, 10.

6. Софизм. 6 = 7. Зрителю предлагается в каждой части записи равенства 6-6 = 7-7 вынести общий множитель: 6(1-1) = 7(1-1). Выражения, стоящие в скобках, получились равные, сократим, получим 6 = 7. В чем ошибка? Объяснение. 1-1 = 0, делить на нуль нельзя.

Исследование заинтересованности учащихся класса математикой и фокусами

Выявив основные закономерности разгадывания и составления фокусов с числами, я провела анкетирование учащихся класса по определению их любимых предметов до и после демонстрации фокусов.

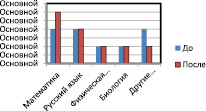
Диаграмма 1 Любимые предметы учащихся 6б класса

После демонстрации фокусов (Приложение) им нужно было ответить еще на вопросы: нравятся ли им фокусы; будут ли они составлять их. Всем учащимся фокусы понравились, 13 учеников из 16 (81,25 %) ответили, что будут составлять фокусы.

Заключение

В литературе описывается множество фокусов с числами, но все они основаны на свойствах чисел, математических закономерностях. При составлении и разгадки фокусов используются следующие закономерности:

1. значение постоянной при счете по кругу (часах) в прямом и обратном направлениях от указанного числа;

2. свойства четности, нечетности чисел;

3. степени числа 2 или двоичная система счисления;

4. свойство последней цифры заданной системы счисления;

5. алгоритмы вычислений, приводящих к заранее известному результату;

6. софизмы.

Данная классификация закономерностей дает возможность не просто удивляться фокусу, а понимать суть его, вооружает способами расшифровки и создания новых фокусов.

Полученные данные могут быть использованы:

- на уроках математики для развития памяти, устного счета, сообразительности, способности мыслить логически;

- на занятиях кружка, факультативных, элективных курсов по математике;

- на математических вечерах.

В результате привлечения внимания учащихся к математике повысилась их заинтересованность в данном предмете, что улучшит их успеваемость.

Я показала свои фокусы на внеклассных занятиях класса. Им было интересно, 81,25 % одноклассников тоже захотели сочинять фокусы.

Мне нравится не только разгадывать, но и придумывать фокусы с числами, изучать удивительный мир чисел.

Приложение 1

Демонстрация фокусов

Фото 1. Отгадывание числа из таблицы

Фото 2. Демонстрация фокусов

Библиографическая ссылка