Введение

Многие взрослые в моём окружении говорили слово «инверсия», и меня стали мучить вопросы: «Что же это такое, инверсия?», «Зачем она нужна?» и «Где используется?». Инверсия есть во многих направлениях от литературы с психологией до математики с физикой. И в каждой дисциплине у неё разное определение, но смысл остаётся один, а именно инверсия — это переворачивание смысла, отрицание или замена белого чёрным. Но сильнее всех меня привлекла геометрическая инверсия и с ней я связала свой проект. Метод инверсии активно изучается с 30 годов прошлого века. Данный метод считается одним из самых действенных среди других способов решения задач на построение. Этот метод более точный, он помогает решать наиболее трудные конструктивные задачи элементарной геометрии, определять конкретное местонахождение нужных фигур. Именно это выделяет его на фоне других методов решения геометрических задач, которые не настолько достоверны. Проблемой моего проекта является конструктивно-производственная задача, с которой сталкиваются многие фирмы в наше время, стремясь сделать работу наиболее продуктивной и так, чтобы она занимала меньше места. Целью моего проекта является решение задачи, которое смогут использовать разные фирмы, для улучшения своей работы. Для выполнения поставленной цели я составила план:

1) изучить основные понятия инверсии;

2) ознакомиться с проблемами, с которыми сталкиваются фирмы в попытках сделать производство компактным и продуктивным;

3) освоить основные преобразования инверсии;

4) рассмотреть конструктивно-производственную задачу и вынести для себя, что может помочь в её решении;

5) сделать математическую модель задачи;

6) найти оптимальный метод решения;

7) решить задачу.

Основная часть

Основные теоремы и свойства.

Точка A2 называется симметричной точке A1 относительно окружности ω с центром O и радиусом R, если точка A2 лежит на луче OA1 и .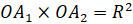

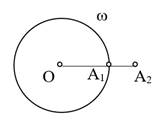
Из определения непосредственно следуют следующие утверждения:

I. Для каждой точки плоскости, кроме центра O, существует единственная точка, симметричная ей относительно окружности w.

II. Для центра O симметричной точки не существует.

III. Если точка A2 симметрична точке A1 относительно окружности w, то и точка A1 симметрична точке A2 относительно окружности w.

IV. Каждая точка, лежащая на окружности w, симметрична сама себе.

V. Если A1 и A2 — различные симметричные точки, то одна из них лежит внутри окружности w, а другая—снаружи.

Основная лемма. Пусть A1, A2 и B1, B2 — пары различных точек, симметричных относительно окружности ω с центром O. Тогда ∠OA1B1 =∠OB2A2.

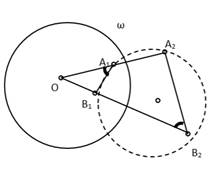
Доказательство.

По определению симметричных точек 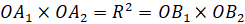, следовательно, 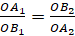. Из пропорциональности сторон следует подобие треугольников OA1B1 и OA2B2 по двум сторонам и углу между ними. Из подобия треугольников следует равенство углов: ∠OA1B1 =∠OB2A2. Равенство этих углов также означает, что четырёхугольник A1A2B2B1 вписанный.

Теорема 1. Прямая, не проходящая через центр инверсии, переходит в окружность, проходящую через центр инверсии.

Доказательство.

Опускается из центра O перпендикуляр OM на данную прямую α, рассматривается точка K, симметричная точке M относительно окружности инверсии. Строится окружность α с диаметром OK. Рассматривается произвольная прямая, не совпадающая с OK, проходящая через центр O и непараллельная прямой a. Пусть она пересекает окружность ω в точке B, а прямую a — в точке A.

Угол при вершине B прямой, поскольку он опирается на диаметр. Из подобия прямоугольных треугольников OBK и OMA получается 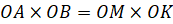. Поскольку точки M и K по построению симметричны, 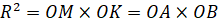. Значит, точки A и B также симметричны относительно окружности инверсии. Следовательно, прямая a и окружность w переходят друг в друга при инверсии.

Теорема 1.1. Окружность, проходящая через центр инверсии, переходит в прямую, не проходящую через центр инверсии.

Теорема 2. Окружность, не проходящая через центр инверсии, переходит в окружность, не проходящую через центр инверсии.

Свойства инверсии:

I. Точки инверсивной окружности ω (O; R) неподвижны.

II. Инверсия сохраняет углы (угол между двумя любыми линиями равен углу между их образами).

III. При рассмотрении инверсии к плоскости прибавляют вымышленную бесконечно удалённую точку K, лежащую на каждой прямой (по определению). Считается, что при каждой инверсии центр O переходит в точку K, также точка K переходит в O.

Задачи на построение при помощи циркуля и линейки.

В задачах на построение с элементами задачи допускаются следующие действия:

1) Выделение точки из множества точек.

I. Произвольную точку на заданной прямой.

II. Точку пересечения двух заданных прямых.

III. Произвольную точку на заданной окружности.

IV. Точки пересечения или касания заданных прямой и окружности.

V. Точки пересечения или касания двух заданных окружностей.

VI. Произвольную точку.

2) Выделение прямой из множеств прямых с помощью линейки.

I. Произвольную прямую, проходящую через заданную точку.

II. Произвольную прямую.

III. Произвольную прямую, проходящую через две заданных точки.

3) Выделение окружности из множества окружностей при помощи циркуля.

I. Произвольную окружность.

II. Произвольную окружность с радиусом, равным расстоянию между двумя заданными точками.

III. Произвольную окружность с центром в заданной точке.

IV. Произвольную окружность с радиусом, равным расстоянию. между двух заданных точек, и центром в заданной точке.

Алгоритм решения задач:

I. Анализ задачи (на этой стадии мы строим модель задачи и ищем оптимальные методы для построения искомый фигуры).

II. Построение (перечисление шагов построения в нужном порядке и выполнение шагов построения).

III. Доказательство (доказать, что полученная фигура, удовлетворяет всем условиям задачи).

IV. Исследование (проверка, что при любых данных в задаче решение останется таким же).

Методы решения задач на построение:

I. Метод гомотетии.

II. Метод поворота.

III. Метод параллельного переноса.

IV. Метод инверсии.

V. Метод подобия.

VI. Метод осевой и центральной симметрии

Решается простая задача для краткого ознакомления с инверсией на практике.

Условие задачи.

Построить окружность, проходящую через две заданные точки А и В, и касающуюся данной окружности w.

Чертёж:

Рассматривается два случая. Если обе точки A и B лежат на окружности ω и, если одна из точек не лежит на окружности.

Если обе точки лежат на окружности, то задача не имеет решения. Отсюда делается вывод, что единственный способ решения, когда одна из точек не лежит на окружности ω. Предполагается, что точка АÏω.

Тогда допускается, что искомая окружность ε построена, тогда при инверсии с центром в точке A точка B перейдёт в точку B?, а окружность ε перейдёт в прямую β, на которой и лежит точка B?. Значит, так как окружность ε касается окружности ω, то прямая β касается окружности ω?. Отсюда составляется построение.

Делается инверсия относительно некоторой окружности λ, у которой центр находится в точке A, отсюда образом точки B будет являться точка B?, также образом окружности ω будет являться окружность ω?.

Дальше проводится прямая β, которая является касательной к окружности ω? и проходит через точку B?.

Проделывается эта инверсия ещё раз, и тогда прямая β перейдёт в окружность ε.

Решение производственно-конструктивной задачи

Условие задачи:

Даны три окружности, каждая из трёх данных окружностей расположена вне двух других. (Для упрощения окружности отмечены разными цветами).

Дано: ω1 (O1; R1) ω2 (O2; R2) ω3 (O3; R3)

Построить: окружность ω

Построение.

I. Проводится прямая α, которая проходит через O1 и O2.

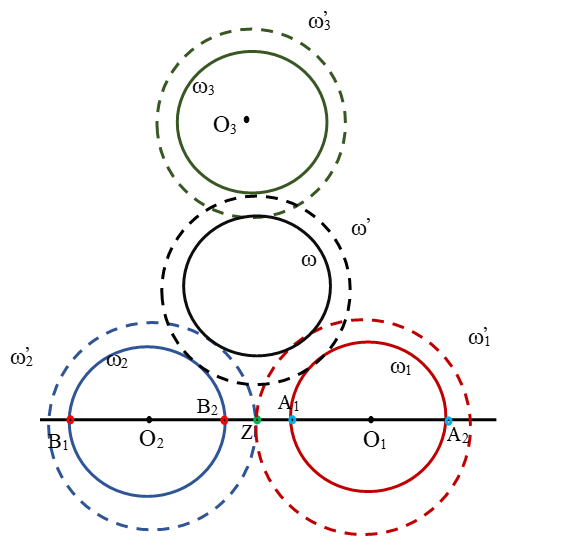
II. Отмечаются точки, в которых прямая α пересекает окружности. Красные точки находящиеся на ω1 обозначим как A1 и А2, аналогично для синих точек. Обозначим их B1 и B2.

III. Определяется самый короткий отрезок из 4. Это отрезок B2A1.

IV. Далее находится середина отрезка B2A1 и обозначается буквой Z.

V. Затем увеличиваются радиусы данных окружностей на отрезок B2Z.

VI. Строятся новые 3 окружности. И обозначаются они как ω?1 (O1; R1+B2Z), ω?2 (O2; R2+B2Z) и ω?3 (O3; R3+B2Z).

VII. Строится окружность ω, для этого принимаем точку Z за центр инверсии, а за радиус произвольный отрезок. Тогда при инверсии две данные окружности ω?1 и ω?2 перейдут в параллельные прямые, а третья окружность ω?3 перейдёт в некоторую окружность или же в прямую. Теперь строится окружность, которая касается параллельных прямых, для этого используется метод геометрических мест.

VIII. Обозначается центр и радиус окружности ω.

IX. Окружность ω и является искомой.

Примечание №1.

Если построить окружность, которая будет концентрической для окружности ω, то она будет касаться данных нам окружностей.

Примечание №2.

Для того, чтобы построить окружность ω, которая касается двух параллельных прямых a и b и данной окружности ω?3, нужно из произвольной точки N, лежащей на прямой a, опустить перпендикуляр NM на прямую b. Через середину K отрезка MN проводим прямую, параллельную прямой a. Строим окружность ω.

Вывод.

В прошлом году меня сильно заинтересовала инверсия. Она показалась мне очень удивительной, потому что этот термин есть не только в математике, но и в литературе, психологии, биологии, химии, геологии, метеорологии, информатике, драматургии и так далее.

Работая над этим проектом, я узнавала много нового и интересного для себя, так, например, я ознакомилась с теорией, в начале она казалась сложной, но после того как я начала решать задачи, она перестала быть таковой. В начале работы было сложно разобраться с чего начать решение задачи, какой метод лучше для этого выбрать. Но я справилась с этими трудностями и выбрала самый простой и оптимальный метод для решения. Мне удалость выполнить все поставленные перед собой задачи, а самое главное, что я добилась цели моей работы. Для того, чтобы распространить свою работу, я написала статью, которая опубликована на сайте. Я надеюсь, что о методе инверсии узнает больше людей, потому что этот метод может помочь людям в проектировке новых промышленных комплексов или жилых районов, в улучшении и расширении промышлености.

Получив решение задачи, его можно применять в разных направлениях, так как его можно подстроить под любой размер конструкции. Поэтому это решение универсально.

Мой интерес к этой теме не исчерпан, и я думаю, что продолжу познавать эту тему уже для себя. И может в будущем, сделаю ещё не одну работу по этой теме.