В 2022 году, в первой части профильного ЕГЭ по математике будет впервые присутствовать 2 задачи на теорию вероятностей. Первая задача (номер 2) не изменится, а вторая (номер 10), по нашему мнению, будет в разы сложнее. Это задача требует более глубокого анализа, и включает несколько шагов, для получения верного ответа. Пример данных задач, был опубликован на официальном сайте «Открытый банк задач ЕГЭ по математике».
Несмотря на то, что это первая часть экзамена (размышление над задачами которой, подразумевает порядка 5 минут времени), здесь встречаются задачи, которые могут быть сложнее всей содержательной части ЕГЭ. Рассмотрим пример одной из таких задач.
«Первый член бесконечной последовательности целых чисел равен 0. Каждый последующий член данной последовательности с вероятностью 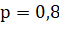 на единицу больше предыдущего, и с вероятностью
на единицу больше предыдущего, и с вероятностью 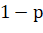 меньше предыдущего. Найдите вероятность того, что среди членов этой последовательности можно найти число
меньше предыдущего. Найдите вероятность того, что среди членов этой последовательности можно найти число  » [1].
» [1].
Есть множество вариантов попадания в  . Рассмотрим некоторые из них (рис.1):
. Рассмотрим некоторые из них (рис.1):
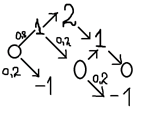
Рис. 1. Математическая модель задачи
1. Возможно, попасть в 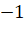 с первого хода. Тогда вероятность равна
с первого хода. Тогда вероятность равна 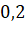
2. 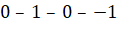 , тогда вероятность равна:
, тогда вероятность равна: 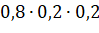
3. 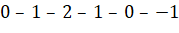 или
или 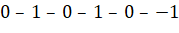 . Здесь, вероятность равна:
. Здесь, вероятность равна: 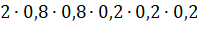 .
.
Но что делать дальше? Ведь этим можно заниматься бесконечно! Начнём с классического способа, заключающегося в нахождении бесконечной суммы ряда (что не входит в школьную программу, за одним исключением – суммы бесконечно-убывающей геометрической прогрессии).
Итак, посчитаем сумму вероятностей попадания в 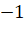 .
.
1. Вероятность попасть из 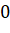 в
в 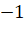 =
= 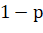
2. Можно из 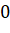 попасть в
попасть в 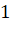 , а затем спуститься в
, а затем спуститься в 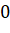 . Вероятность будет равна
. Вероятность будет равна 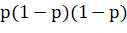
3. Попасть в 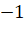 можно также с вероятностью:
можно также с вероятностью: 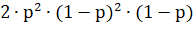
Так можно считать до бесконечности. Получаем следующее выражение:
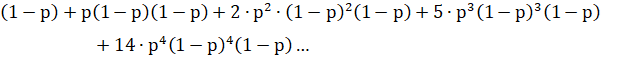
Нахождение способов подняться до 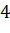 , а потом спустить до
, а потом спустить до 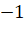 уже вызывает проблемы. В связи с этим просто посчитать сумму ряда, по крайней мере со знаниями школьной программы не видится возможным. Соответственно, классический способ решения на этом заканчивается и не даёт никакого решения.
уже вызывает проблемы. В связи с этим просто посчитать сумму ряда, по крайней мере со знаниями школьной программы не видится возможным. Соответственно, классический способ решения на этом заканчивается и не даёт никакого решения.
Приходится искать альтернативные методы решения, и такие, как оказалось, есть. Первый – заключается в привлечении расширенных знаний по комбинаторике, а второй с широким кругозором знаний различных математических головоломок. Начнём с первого.
Очевидно, что нам мешает старший коэффициент, выражающий количество способов подняться до 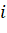 -го числа и опуститься до
-го числа и опуститься до 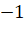 . Обозначим количество этих способов коэффициентом
. Обозначим количество этих способов коэффициентом 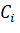 .
.
Тогда, например, количество способов подняться до 4 и опуститься до 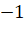 будет обозначено, как
будет обозначено, как 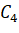 .
.
Перепишем наше выражение, полученное суммированием:
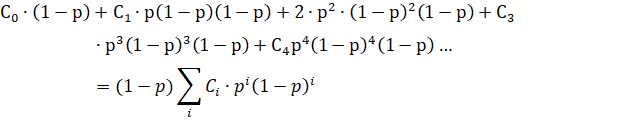
Теперь, используем знания комбинаторики [2, 3]. Оказывается, что у наших коэффициентов 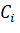 есть название - числа Каталана.
есть название - числа Каталана.
Числа Каталана 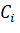 – это количество правильных скобочных последовательностей длины
– это количество правильных скобочных последовательностей длины 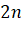 , то есть таких последовательностей из
, то есть таких последовательностей из 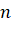 левых и
левых и 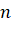 правых скобок, в которых количество открывающихся скобок равно количеству закрывающихся. То есть ((())) или (())().
правых скобок, в которых количество открывающихся скобок равно количеству закрывающихся. То есть ((())) или (())().
Теперь, для решения нашей задачи, требуется воспользоваться производящей функцией. Данное понятие выходит далеко за рамки школьной программы, а также программы некоторых высших учебных заведений. Благо в данном контексте, глубокое понимание данного термина не требуется, однако его привлечение вызывает множество вопросов.
Стоит отметить, что данную функцию можно вывести, как показано, например в [4]. Но, по нашему мнению, процесс вывода достаточно трудоемкий, и точно не имеет место быть на экзамене, когда на счету каждая минута. Итак, воспользуемся производящей функцией для чисел Каталана [4]:
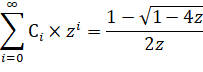
Теперь, с помощью данной функции, мы можем найти сумму ряда без значительных проблем.
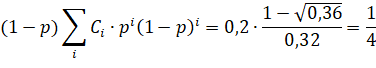
Ответ получен, однако сколько времени для его получения бы затратил среднестатистический школьник? Отметим, также, что данный способ решения избавляет от следующей проблемы.
Если поменять вероятности 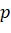 и
и 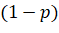 местами, т.е. мы будем удаляться от
местами, т.е. мы будем удаляться от 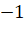 с меньшей вероятностью, то мы получим в ответе 1.
с меньшей вероятностью, то мы получим в ответе 1.
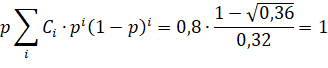
Когда мы будем рассматривать следующий способ, мы заметим, что у нас будет два ответа и выбор из них – проблема.
Итак, рассмотрим второй способ решения, за счёт широкого кругозора. В книге Мостеллера [5] была приведена следующая задача «На краю утеса» (рис. 2):
Есть пьяница, стоящий на обрыве. С вероятностью 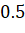 он каждую секунду делает шаг вправо или влево. Какая вероятность того, что когда-нибудь он упадет?
он каждую секунду делает шаг вправо или влево. Какая вероятность того, что когда-нибудь он упадет?

Рис. 2. Вырезка из книги.
Опустим полное решение, описанное в данной книге, и приведём её урезанный вариант.
Вероятность того, что он упадет из точки 0 - 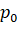 . Из точки 1 -
. Из точки 1 - 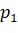 , а из точки 2 -
, а из точки 2 - 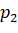 (рис. 3). Что же должно произойти, чтобы человек свалился?
(рис. 3). Что же должно произойти, чтобы человек свалился?
1. Гуляя, человек должен оказаться в точке 0
2. А после этого, он должен упасть
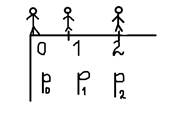
Рис. 3. Иллюстрация к задаче.
Какова вероятность того, что человек из единицы попадет в ноль? Заметим, что мы можем мысленно сдвинуть обрыв, получая тем сам аналогичную задачу (отметим, что это возможно благодаря тому, что ряд бесконечный, и сдвиг или удаление/добавление ограниченного количества элементов не меняет предел). Соответственно, вероятность упасть из позиции 1 есть вероятность того, что мы когда-нибудь сместимся на шаг назад, т.е.  . Это вероятность того, что человек сместится влево. Получаем, что
. Это вероятность того, что человек сместится влево. Получаем, что 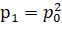 ,
, 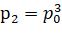 и.т.д... Значит, нам осталось лишь найти
и.т.д... Значит, нам осталось лишь найти 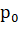 .
.
Находясь в точке 0, человек может сразу пойти влево, или же сделать шаг вправо, а потом когда-нибудь влево. Тогда мы получаем равенство, зная, что 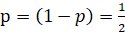 .
.
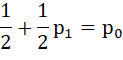
Теперь, решим полученное равенство, пользуясь тем, что 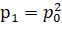 :
:
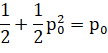
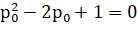
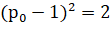
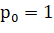
Это означает, что как бы далеко от обрыва не стоял человек, рано или поздно он упадет. Заметим, что, данное рассуждение достаточно сложно провести, не зная его заранее. Также стоит отметить, что в данной задаче вероятности 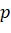 и
и 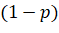 были равны. Посмотрим, что будет в нашем случае.
были равны. Посмотрим, что будет в нашем случае.
Вернемся к исходной задаче (рис. 1). Какова вероятность попасть в 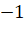 ? Можно сразу из точки
? Можно сразу из точки 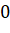 попасть в
попасть в 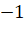 , а можно сначала попасть в
, а можно сначала попасть в 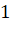 , потом в
, потом в 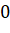 , а потом в
, а потом в 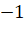 :
:
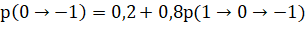
Вероятность попасть из единицы в минус единицу, по аналогии с данной задачей, будет равна 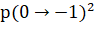
Выполнив замену, получаем равенство:
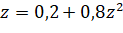
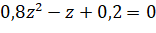
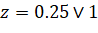
Итак, мы получаем два ответа, причём правильным из них оказывается 0,25. Но почему?
Насколько нам известно, ответ будет зависеть от следующего частного 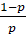 . В случае, если его значение больше 1, в ответе всегда получится 1 (что автоматически решает задачу, еще на стадии её задания, и моментально выписывается ответ, целесообразность чего мы не понимаем), если же значение меньше 1, как в нашем случае (
. В случае, если его значение больше 1, в ответе всегда получится 1 (что автоматически решает задачу, еще на стадии её задания, и моментально выписывается ответ, целесообразность чего мы не понимаем), если же значение меньше 1, как в нашем случае (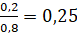 ), то мы получаем ответ.
), то мы получаем ответ.
Отметим, что данный вывод достаточно очевиден, если понимать основы случайных процессов (также не проходящихся в школьной программе). В случае если частное больше 1, подразумевается, что вероятность спуститься ниже выше, а следовательно, в среднем, на каждый шаг вверх, приходится 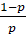 шагов вниз. В таком случае, очевидно, что мы всегда достигнем значения
шагов вниз. В таком случае, очевидно, что мы всегда достигнем значения 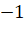 , сколь долго мы бы не удалялись от него.
, сколь долго мы бы не удалялись от него.
В обратном случае ситуация противоположная, и шанс опуститься до 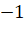 снижается в зависимости от уменьшения значения
снижается в зависимости от уменьшения значения 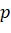 .
.
На фоне этого, возникает максимально оптимальный вариант решения данной задачи – алгоритмический. Алгоритм, следующий:
Рассмотрим частное 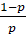 , ответом
, ответом 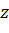 будет следующее значение:
будет следующее значение:
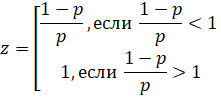
Отметим, что данный способ полностью обесценивает какие-либо рассуждения данной задачи, и позволяет, даже не читать задачу, а просто записать ответ, что очевидно, не соответствует уровню итогового экзамена, проверяющего знания.
В заключении отметим, что большинство элементов, рассмотренных в данной статье отсутствуют в подавляющем числе школьных учебников, что напрямую увеличивает нагрузку как на педагогов, за счёт поиска и подготовки данного материала, а также сложность грамотной передачи знаний в головы учащихся, а также увеличивает нагрузку на учащихся в плане восприятия новой для них информации, и форсированного расширения кругозора знаний.
Использование же последнего приведённого способа, помимо обесценивания задачи, приводит также к банальной зубрежке формулы, что для изучения математики грозит резким снижением качества образования.
