Введение

Поводом к написанию данной работы послужили следующие исторические факты:

1) в научной литературе зафиксировано более 300 доказательств теоремы Пифагора. ТеоремаПифагоразаслужила место в «Книге рекордов Гиннеса» как имеющая наибольшее число доказательств разными способами: через подобие треугольников, методом площадей, доказательство через равнодополняемость и равносоставленность, методом разложения;

2) к доказательству этой теоремы обращались математики разных исторических периодов и не только математики. Причина популярности, триумфа теоремы Пифагора заключается вединстве простоты, красоты и значимости. Она проста, но не очевидна. Это придает ей особую притягательную силу.

Актуальность исследования заключается в том, что в работе рассматриваются такие способы доказательства известной теоремы, о которых в школьных учебниках даже не упоминается, но они вызывают интерес своей простотой и изяществом, значительно расширяют знания о теореме Пифагора и применении ее геометрических доказательств в жизни.

Цель работы: установить некоторые геометрические способы доказательства теоремы Пифагора, основанные на равносоставленности фигур, и найти их применение в создании головоломок.

Задачи работы:

1) проанализировать информацию по теме работы;

2) установить, где применяется метод равносоставленных фигур;

3) изготовить геометрические головоломки «СМОТРИ: ТЕОРЕМА ПИФАГОРА!» из подручных материалов и в ИГС GeoGebra;

4) попытаться найти собственные доказательства теоремы Пифагора.

Предмет исследования: некоторые доказательства теоремы Пифагора методом разложения.

Гипотеза: выполнив работу, будут установлены различные геометрические доказательства теоремы Пифагора; выполнив анализ и сравнение различных доказательств, можно будет найти практическое применение некоторых из них.

О теореме Пифагора написано огромное количество научной литературы, рефератов, статей, которые использовались для написания работы. Врассмотренной литературе вопрос практического применения теоремы Пифагора освещён недостаточно. При анализе источников информации возникли вопросы: как объяснить, что существует такое множество доказательств одного и того же математического утверждения; где в реальной жизни могут найти применение эти геометрические доказательства. Чтобы ответить на эти вопросы, в работе рассмотрены некоторые способы доказательства теоремы из различных источников.

Для раскрытия темы работы автором была сделана попытка доказать теорему собственными способами по аналогии с древними доказательствами, которые сопровождались только указанием «СМОТРИ!». Кроме того, наосновании найденной информации было создано несколько головоломок «СМОТРИ: ТЕОРЕМА ПИФАГОРА!».

Методы исследования: анализ учебников, справочной математической литературы; построения с помощью циркуля и линейки; компьютерное моделирование математических объектов с помощью ИГС GeoGebra; анализ, сравнение, сопоставление и обобщение объектов, полученных в результате моделирования; проверка выдвинутых гипотез; аналитические рассуждения.

Теорема Пифагора и её доказательства

Существует огромное количество методов доказательства теоремы Пифагора. Одним из основных является метод равносоставленных фигур (метод разложения), накоторый сделан акцент в работе. Он базируется наравновеликости и равносоставленности многоугольников.

Метод равносоставленных фигур широко применяется вгеометрии: при выводе формул площади параллелограмма, треугольника, трапеции; при нахождении площади «клетчатого многоугольника». Применяется этот метод и в играх-головоломках на складывание фигур: головоломки «Пифагор» и «Танграм».

Первое наглядное доказательство теоремы Пифагора автор узнал в 6 классе, когда науроках «Наглядной геометрии» было предложено доказать, что квадрат, прилегающий к гипотенузе равнобедренного треугольника, равен сумме квадратов, прилегающих к катетам. Тогда это было доказано путём проведения диагоналей квадратов [8].

Позже, на уроках геометрии в 8 классе теорема Пифагора была доказана для произвольного прямоугольного треугольника с помощью достраивания треугольника с катетами a и b до квадрата со стороной (a+b) (рис. 1).

На уроке были установлены три эквивалентные формулировки теоремы [6], [7]:

1) в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов;

2) площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах;

3) квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

После изучения данной теоремы на уроках геометрии возникли вопросы: так ли её доказывали во времена Пифагора, и существуют ли другие доказательства этой теоремы?

Согласно различным источникам, существует более 370различных доказательств теоремы Пифагора [2]. На сайте https://www.cut-the-knot.org/pythagoras/ описаны и доказаны 122различных способа доказательства.

После просмотра различных доказательств для более подробного рассмотрения были выбраны те, которые основаны на равновеликости фигур, именно их, по предположению, можно использовать в практических целях.

Некоторые доказательства, основанные на равносоставленности:

1)Древнекитайское доказательство [11].

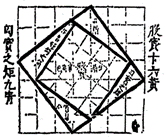
Самым древним доказательством теоремы Пифагора считается чертёж в древнекитайском трактате «Чжоу-би суань цзинь». Там теорема была рассмотрена дляегипетского треугольника с гипотенузой 5 и катетами 3, 4 единиц измерения (рис. 2).

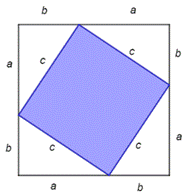
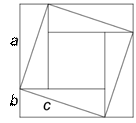
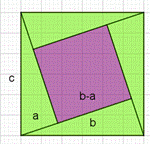
Также в энциклопедии знаний древнекитайскихматематиков «Математика в девяти книгах», которая была создана во II веке до н. э., теорема Пифагора была доказана с помощью чертежа, на котором 4 равных прямоугольных треугольника со сторонами a и b образуют 2квадрата. Сторона внешнего квадрата равна (a+b), а внутреннего – c (рис. 3).

Если из внутреннего квадрата вырезать 2прямоугольных треугольника и приложить их к гипотенузам двух других треугольников, то получится фигура, состоящая издвух квадратов со сторонами a и b. Значит, c2=a2+b2 (рис.3 ).

2)Доказательство Евклида.

В III веке до н.э. в первой книге «Начал» Евклид предложил своё доказательство теоремы. Его долгое время использовали для доказательства теоремы Пифагора в школе (в середине ХХ века). Однако оно является довольно громоздким. Доказательство теоремы Пифагора Евклидом представлено в школьном учебнике по геометрии Киселёва А.П. [9].

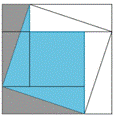
Евклид приводит и графическое доказательство, где квадраты, выстроенные на катетах, превращаются в параллелограммы той же площади (так как они имеют то же основание и ту же высоту), а те, в свою очередь, трансформируются в квадрат, построенный на гипотенузе [12] (рис. 4).

3)Доказательство математиков IX века [11].

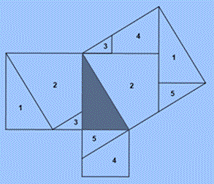
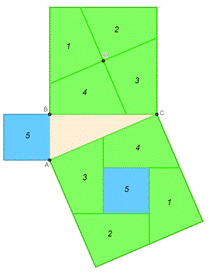
Математики IX века предлагали следующий чертёж. На нём квадраты, построенные на катетах, расположены ступенями, один рядом с другим. Также построен квадрат со стороной, равной гипотенузе. Индусы назвали такую композицию «стулом невесты». На чертеже общая часть квадратов – шестиугольник 4. Равенство треугольников 1, 2 и 3 доказывается параллельным переносом. Таким образом, квадраты, построенные на катетах, состоят из тех же частей, что и квадрат нагипотенузе. Значит, квадрат на гипотенузе равен сумме квадратов на катетах (рис. 5).

4)Доказательство Аннариция [11].

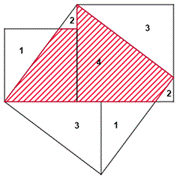
В X веке Аннариций (ан-Найризий) вкомментариях к «Началам» Евклида дал своё доказательство теоремы Пифагора. В своём чертеже Аннариций разбил квадрат, лежащий на гипотенузе, на 5 частей (3 треугольника и 2 четырёхугольника), из которых можно составить квадраты на катетах (рис. 6). Равенство отдельных фигур доказывается с помощью параллельного переноса.

Доказательство Аннариция можно считать одним из простейших геометрических способов доказательства теоремы Пифагора, так как в нём квадрат на гипотенузе разбивается всего на 5 частей.

5) Доказательство Перигаля [11].

На чертеже Генри Перигаля (чертёж нередко называют «колесо с лопастями») через центр квадрата, построенного на большом катете, проведены 2 прямые: одна из них перпендикулярна, а другая параллельна гипотенузе.

Из полученных 4-х четырёхугольников и квадрата, построенного на маленьком катете, можно параллельным переносом составить квадрат на гипотенузе (рис. 7).

6)Древнеиндийское доказательство.

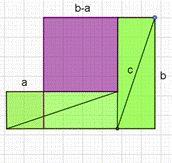
В трактате «Сиддханта широмани» древнеиндийского математика XIIвека Бхаскары есть ещё один чертёж, доказывающий теорему Пифагора. Нанём изображена внутренняя часть древнекитайского чертежа. В пояснение крисунку написано только одно слово: «СМОТРИ!». С помощью данного чертежа теорему Пифагора можно доказать, как геометрическим, так и алгебраическим способом.

Доказательство (рис. 8) [11]: данный квадрат состороной c можно переложить в 2 квадрата: один состороной a, другой со стороной b. А это значит, что c²=a²+b².

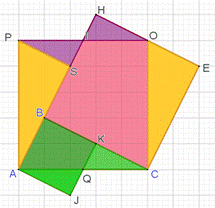
7) Доказательство Леонардо Да Винчи [12].

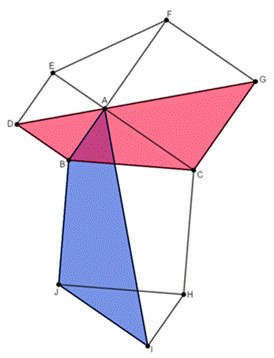
Теорема Пифагора привлекла даже известного художника и учёного, Леонардо Да Винчи, который предложил своё доказательство. На его чертеже построены 2 треугольника, равных данному, один на стороне квадрата гипотенузы, другой на сторонах квадратов катетов (рис. 9). Отрезок AI делит квадрат BCHJ на две одинаковые части. Повернув ABJI на 90° против часовой стрелки, можно заметить, что ABJI=DBCG. Значит, с одной стороны, площадь закрашенной фигуры равна сумме половин площадей квадратов, построенных на катетах, и площади исходного треугольника. С другой стороны, она равна сумме половины площади квадрата, построенного на гипотенузе, и площади исходного треугольника. Из этого следует, что квадрат на гипотенузе равен сумме квадратов на катетах: c² = a² + b².

8)Доказательство Пауля Софуса Эпштейна. [10]

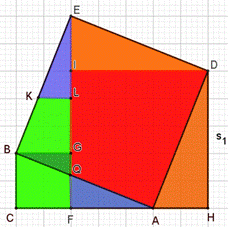
В ХХ веке Пауль Софус Эпштейн – немецкий математик (основные труды Эпштейна относятся к теории чисел и истории математики) представил своё доказательство знаменитой теоремы.

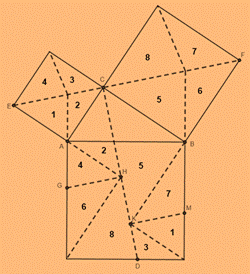
В доказательстве Эпштейна (рис. 10) квадрат на гипотенузе разбивается на 8 треугольников. На рисунке точка C принадлежит отрезку EF, отрезок CD перпендикулярен EF, отрезки GH и KM параллельны EF. Равенство отдельных фигур доказывается при помощи параллельных переносов и поворотов треугольников, например, треугольники 2 совпадают при повороте друг друга на 90°, а треугольники 3 совпадают при осевом отображении относительно оси EF и параллельном переносе. Преимуществом данного метода является то, что квадраты разбиваются только на треугольники.

Игры-головоломки, основанные на теореме Пифагора

После установления различных способов доказательства теоремы Пифагора была сделана попытка найти их практическое применение. Источником вдохновения стали головоломки «Пифагор» и «Танграм». Возникла идея: создать свою коллекцию головоломок, с помощью которых можно доказать теорему Пифагора.

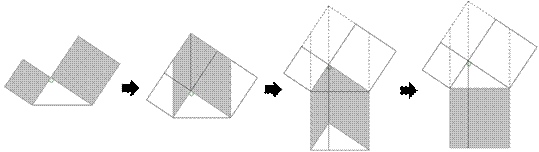
При создании головоломок было замечено, что в древних трактатах нет словесного доказательства, в пояснениях к рисункам было только указание: «СМОТРИ!». Было решено пойти по этому же пути: «СМОТРИ!». Первые игры-головоломки были созданы из картона. Однако эта работа требует много времени и сил. Поэтому было решено создать головоломки в ИГС GeoGebra. Эти игры вызвали интерес у учеников 8–9-х классов.

Суть игр-головоломок заключается в том, что фигуры, на которые разбиты квадраты, построенные на катетах надо «перетащить» в квадрат, построенный на гипотенузе (или наоборот, фигуры с квадрата, построенного нагипотенузе, нужно перетащить на квадраты, построенные на катетах) спомощью инструмента «Перемещать» ИГС Geogebra. Всего было создано 11игр- головоломок.

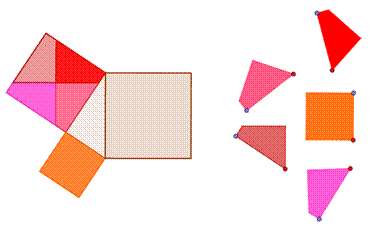
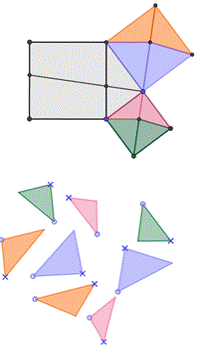
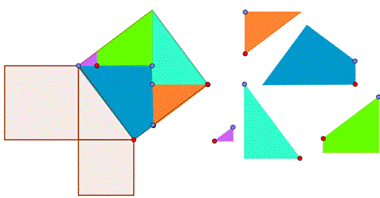
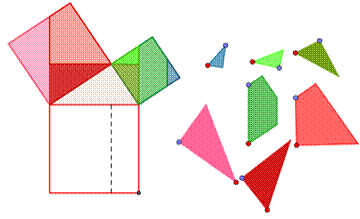
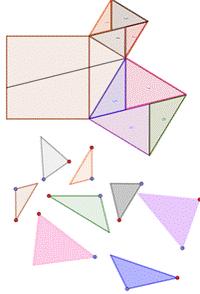
Авторские способы применения метода равносоставленных фигур придоказательстве теоремы Пифагора

После создания головоломок была предпринята попытка найти собственные способы доказательства теоремы Пифагора методом равносоставленных фигур.

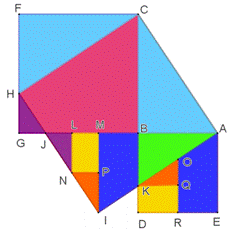
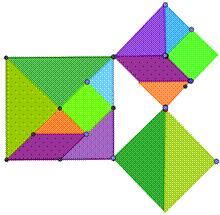
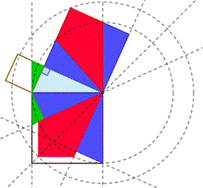
Первый способ разложения на части квадратов, построенных на сторонах прямоугольного треугольника, не дал результата (рис. 11).

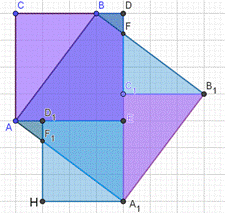
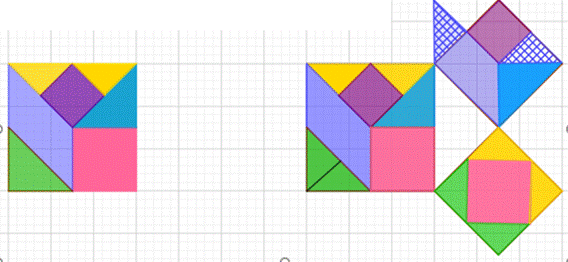
Позже возникла идея. В рассмотренных доказательствах квадраты были расположены во внешней области данного прямоугольного треугольника. А что будет, если квадраты будут построены по другую сторону от катетов и гипотенузы треугольника? Как оказалось в ходе моделирования в ИГС Geogebra, с помощью данного построения также можно доказать теорему Пифагора методом равносоставленных фигур. Ниже представлены некоторые из 10 найденных способов доказательства теоремы Пифагора, основанных на равносоставленности фигур.

Также теорему Пифагора удалось доказать с помощью игры «Танграм» и головоломки «Пифагор» (если сделать дополнительные построения), но только для равнобедренного прямоугольного треугольника. На основании этих доказательств в ИГС «GeoGebra» созданы динамические головоломки.

Заключение

В результате выполнения работы гипотеза подтвердилась, цель работы была достигнута, задачи решены.

Было установлено:

- многочисленные доказательства теоремы Пифагора являются нетолько математическим интересом. Изобретательный подход, элегантность, красота этих доказательств вызывает восхищение;

- теорема Пифагора является классическим примером «единомыслия» ? это математическое утверждение присутствует практически во всех древних культурах, это одна из самых известных в мире теорем, и она неразрывно связана с именем Пифагора;

- доказательством этого математического утверждения занимались нетолько математики, но и художник и учёный Леонардо Да Винчи, немецкий физик Иоганн Эдуард Бетхер, Президент США Джеймс Абрам Гарфилд и Президент Австрии Курт Вальдхейм;

- большое число доказательств теоремы Пифагора объясняется тем, что умение доказывать данную теорему стало со временем универсальным показателем общего образования человека.

На основании анализа геометрических методов доказательства теоремы было изготовлено несколько головоломок «СМОТРИ: ТЕОРЕМА ПИФАГОРА!» изподручного материала (картона) и в электронном виде (вИГСGeoGebra).
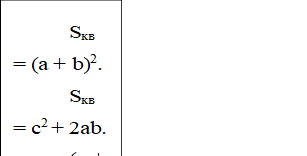