Введение
Общепризнанно, что умение рассуждать и логически мыслить чрезвычайно сильно развивается в процессе изучения математики, быть может, сильнее, чем в процессе изучения других школьных предметов. В этой ситуации на учителя математики ложится основная нагрузка по формированию у школьников логической грамотности. В свою очередь владение элементарным комплексом логических понятий и действий позволяет школьникам лучше усваивать математику.
Цель: развитие способностей умения рассуждать и делать правильные выводы через логические задачи
«Рыцари и лжецы» (5-8 класс)
Задача 1
На улице, став в кружок, беседуют четыре девочки: Аня, Валя, Галя и Надя. Девочка в зелёном платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Кто какое платье носит?
Решение:
Аня Валя Галя Надя
бел. гол. зел. роз.
Девочка в зелёном платье (не Аня и не Валя) стоит между Надей и девочкой в голубом платье. Галя в зелёном, Валя в голубом; 2) Девочка в белом платье стоит между девочкой в розовом платье и Валей. Надя в розовом, Аня в белом.
Ответ: Аня в белом, Валя в голубом, Галя в зелёном, Надя в розовом.
Задача 2
К третьей группе из четырёх аборигенов вы обратились с вопросом: «Сколько рыцарей среди вас?» На этот вопрос они дали такие ответы. Первый: «Все мы лжецы», второй: «Среди нас один лжец», третий: «Среди нас два лжеца», четвёртый: «Я ни разу не солгал и сейчас не лгу». Сможете ли вы определить, кем являлся четвёртый абориген?
Решение:
Первый не может быть рыцарем. (Если бы он был рыцарем, то говорил бы правду; но он говорит, что все лжецы, в том числе и он сам.) Значит первый — лжец. Если второй — рыцарь, то он говорит правду, и, поскольку первый — лжец, то второй, третий и четвертый — рыцари. Но слова третьего противоречат словам второго, значит, они не могут быть рыцарями одновременно. Поэтому второй — тоже лжец. Если третий — лжец, то четвёртый — рыцарь (если он тоже лжец, то первый сказал правду, что неверно). Если же третий — рыцарь, то лжецов двое. Нам известно, что первый и второй — лжецы, а значит, четвёртый и в этом случае — рыцарь.
Ответ: Рыцарем
Задача 3
После обеда, вы вышли в сад, где группами стояли и разговаривали островитяне. Вы подошли к одной такой группке из островитян Антонио, Бена и Стива. На ваш вопрос кто они такие, Бен ответил: «Мы все лжецы», а Стив сказал: «Среди нас только один рыцарь». Сможете ли вы определить, кто из этих троих кто?
Решение:
Бен не может быть рыцарем: рыцарь не сказал бы, что все они лжецы. Значит, Бен лжец. Тогда среди Антонио и Стива один или два рыцаря. Если Стив лжец, то среди них двое рыцарей, чего быть уже не может, так как Бен и Стив лжецы. Значит, Стив рыцарь; поскольку он говорит правду, то он и является единственным рыцарем.
Ответ: Антонио и Бен — лжецы, Стив — рыцарь.
Задача 4
Не ограничившись одним ответом, вы опросили всех аборигенов, собравшихся в порту, и все они ответили: «Все остальные собравшиеся — лжецы». Сколько рыцарей собралось в порту?
Решение:
Если в порту нет ни одного рыцаря, то получается, что все говорят правду, но тогда они не могут быть лжецами. Если рыцарей больше одного, то каждый рыцарь лжёт, потому что кроме него самого есть ещё хотя бы 1 рыцарь. Значит, рыцарь один: в этом случае действительно все лжецы лгут, а единственный рыцарь говорит правду.
Ответ: Один.
Задача 5
Гуляя по городу, вы услышали интересный диалог. Один из аборигенов сказал другому: «По крайней мере один из нас — рыцарь». «Ты — лжец», — ответил ему второй. Кто из них кто?
Решение:
Если второй — рыцарь, то он говорит правду, поэтому первый — лжец. Тогда среди них есть хотя бы один рыцарь, что и сказал первый; но первый — лжец и не может говорить правду. Значит, второй является лжецом. А поскольку второй лжёт, первый — рыцарь.
Ответ: Первый — рыцарь, а второй — лжец
Задача 6
В конференции по вопросам белой и черной магии участвовало 100 фей и ведьм. Каждой участнице был задан вопрос: «Если не считать Вас, то кого больше среди остальных участниц – фей или ведьм?». Когда опросили 51 участницу, и все ответили, что ведьм больше, опрос прервали. Ведьмы всегда лгут, а феи всегда говорят правду. Сколько фей среди участниц?
Решение:
Все феи должны ответить одинаково, и все ведьмы – тоже. Если больше фей, то феи так и скажут, но среди 51 опрошенных обязана найтись фея; противоречие. Если же больше ведьм, то все они соврут, то есть скажут, что больше фей, и среди 51 опрошенных хотя бы одна – ведьма.
Ответ: 50 фей.
Задача 7
Как-то встретились мудрец, хитрец и лжец. (Известно, что мудрец всегда говорит правду, лжец – лжет, а хитрец, если ему сказали правду, говорит правду, если ложь – лжет, а если он говорит первый, то он лжет.) Между ними состоялся разговор:
Первый сказал второму: «Ты – хитрец».
Второй ему ответил: «Ты лжешь, это ты – хитрец».
На что третий возразил: «Вы оба лжете, хитрец – это я!».
Определите, кто из них мудрец, хитрец и лжец.
Решение:
Рассмотрим все возможные варианты для Первого.1) Если Первый лжец, то из первого высказывания следует, что Второй может быть только мудрецом, но тогда из второго утверждения следует, что Первый хитрец. Противоречие.2) Если Первый мудрец, то второй хитрец. А так как второму сказали правду, то он должен сказать тоже правду. Но в таком случае его высказывание ложно. Противоречие.3) Остается случай когда Первый хитрец. В этом случае второе утверждение истинно, то есть Второй -мудрец. Тогда Третий -лжец. Этот случай удовлетворяет условию задачи.
Ответ: Первый –хитрец, Второй –мудрец, Третий –лжец.
Задача 8
В зоомагазине на жердочке сидят три попугая – правдивый (всегда говорит правду), хитрец (может сказать правду, а может солгать) и лжец (всегда лжет). Причем сидят они именно в таком порядке. Хозяин хочет выяснить, в каком порядке они сидят, и задает каждому по очереди вопрос: «Кто сидит в центре?» Что должен ответить хитрец, чтобы его нельзя было вычислить?
Решение,
Попугай который всегда говорит правду, на вопрос «Кто вы?» естественно ответит «я честный попугай». Получается «С» и есть честный попугай. Попугай который всегда врет никогда не скажет про себя «Я лжец». Т. к. честный попугай определен, то ответ попугая который всегда врет – «Я хитрец». Это попугай «В». Ну и методом исключения, попугай-хитрец находится под буквой «А».
Ответ: «Правдивый»
Задача 9
В Пусоземье живут три племени: эльфы, гоблины и хоббиты. Эльф всегда говорит только правду, гоблин всегда лжёт, а хоббит через раз говорит то правду, то ложь. Однажды за круглым столом пировало несколько пустоземцев, и один из них сказал, указав на своего левого соседа: «Он – хоббит». Сосед сказал: «Мой правый сосед солгал». В точности ту же фразу затем повторил его левый сосед, потом её же произнёс следующий по кругу, и так они говорили «Мой правый сосед солгал» много-много кругов, да и сейчас ещё, возможно, говорят. Определите, из каких племён были пирующие, если известно, что за столом сидело девять жителей Пустоземья.
Решение,
Рассмотрим того, про кого сказали, что он - хоббит, и для удобства назовём его Боб. Боб не согласился с тем, что он хоббит, следующий не согласился с ним, а значит, подтвердил, что Боб хоббит, и так далее - все говорящие через раз подтверждали или отрицали, что Боб хоббит. Если пирующих было 9 (нечётное число), то на следующем круге каждый говорил противоположное к тому, что сказал на предыдущем, так что все они хоббиты, а первый хоббит про Боба сказал сначала правду, что вполне возможно. Мы решили пункт а) задачи. Для решения пункта б) заметим, что, поскольку 10 - чётное число, то говорящие на каждом круге говорят одно и то же, поэтому хоббитов среди них нет. Тогда и Боб - не хоббит, а сказавший так про него его правый сосед солгал, то есть он гоблин. Сам же Боб уличил гоблина во лжи, так что он эльф. Его сосед слева снова гоблин, и так далее - за столом сидят, чередуясь, пять гоблинов и пять эльфов.
Ответ: Все были хоббитами
«Анализ утверждений» (9-10 класс)
Задача 1
Какие из приведённых ниже утверждений равносильны утверждению «Если Вы ? слон, значит, Вы ничего не забываете»?
(1) Если Вы ? не слон, значит, Вы все забываете.
(2) Если Вы что-то забываете, значит, Вы ? не слон.
(3) Если Вы ? не слон, значит, Вы что-то забываете.
(4) Если Вы ничего не забываете, значит, Вы ? слон.
В ответе укажите номера выбранных Вами утверждений без пробелов, запятых и других дополнительных символов.
Задача 2
Пять жильцов многоквартирного дома — Андрей, Борис, Виктор, Денис и Егор — имеют различный возраст. При этом известно, что возраст Андрея больше, чем сумма возрастов Бориса и Виктора, Виктор старше Дениса, но младше Егора. Выберите утверждения, которые следуют из приведённых данных.
1) Андрей старше Дениса
2) Андрей самый старший из жильцов
3) Егор старше Бориса
4) Борис старше Егора
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задача 3
В 2013 году в городе N цена на молоко повысилась на 5% по сравнению с 2012 годом, а в 2014 году — повысились на 7% по сравнению с 2013 годом. Какие из приведённых ниже утверждений следуют из этих данных?
(1) В 2015 году цена на молоко повысится примерно на 9% по сравнению с 2014 годом.
(2) В 2015 году рост цены должен прекратиться.
(3) За два года цена выросла на 13% по сравнению с 2012 годом.
(4) Ни одно из предложенных.
В ответе укажите номера выбранных Вами утверждений без пробелов, запятых и других дополнительных символов.
Задача 4
Известно, что все щуки — рыбы, также известно, что все рыбы плавают в воде. Тюлень тоже плавает в воде. Выберите утверждения, которые следуют из приведённых данных.
1) Все тюлени — рыбы
2) Если животное не плавает, то это не тюлень
3) Все щуки плавают в воде
4) Если животное плавает в воде, то оно либо рыба, либо тюлень
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задача 5
Автолюбителям известно, что если в присутствии инспектора ГИБДД проехать на красный свет, то штраф неминуем. Выберите утверждения, которые непосредственно следуют из этого знания.
1) Если вас не оштрафовали, вы не проезжали на красный свет.
2) Если вас оштрафовал инспектор, то вы проехали на красный свет.
3) Если вы проехали на красный свет с не пристёгнутым ремнём, то заметивший это инспектор ГИБДД вас оштрафует.
4) Если вы не проезжали на красный свет, то вы не будете оштрафованы.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
Ответ |
4 |
1 |
4 |
23 |
3 |
«Среднее арифметическое в задачах» (10-11 класс)
Задача
На доске написано более 42, но менее 54 целых чисел. Среднее арифметическое этих чисел равно −7, среднее арифметическое всех положительных из них равно 6, а среднее арифметическое всех отрицательных из них равно −12.
а) Сколько чисел написано на доске?
б) Каких чисел больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение.
a) Напомним, что среднее арифметическое нескольких чисел есть сумма этих чисел, делённая на их количество. Пусть на доске написано n чисел. Тогда их сумма: S = −7n. Обозначим: p — количество положительных чисел, m — количество отрицательных чисел, z — количество нулей. Таким образом, n = p + m + z.
Пусть S+ и S− — суммы положительных и отрицательных чисел соответственно. Имеем:
S+ = 6p, S− = −12m, и так как S = S+ + S−, то: −7n = 6p − 12m. Правая часть данного равенства делится на 6. Поскольку 6 и 7 взаимно просты, число n делится на 6. Между числами 42 и 54 есть только одно такое число: n = 48.
Ответ: одно - 48
б) Из равенства −7 · 48 = 6p − 12m получаем после сокращения на 6: 2m − p = 56. Кроме того: p + m + z = 48. Сложим полученные равенства: 3m + z = 104. Так как 104 при делении на 3 дает остаток 2, число z также даёт остаток 2: z = 3k + 2. Отсюда: 3m + 3k + 2 = 104, или m = 34 − k.
Соответственно, p = 2m − 56 = 2(34 − k) − 56 = 12 − 2k.
Составляем разность: p − m = (12 − 2k) − (34 − k) = −22 − k < 0, так что p < m — отрицательных чисел написано больше.
Ответ: отрицательных чисел написано больше.
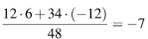в) Из равенства p = 12 − 2k видим, что p< 12. Приведём пример с p = 12 (тогда k = 0, z = 2, m = 34). Пусть написано 12 чисел 6, 34 числа −12 и два нуля. Этот набор удовлетворяет условию задачи: среднее арифметическое положительных чисел равно, очевидно, 6; среднее арифметическое отрицательных чисел равно −12, а среднее арифметическое всех чисел:
Следовательно, наибольшее возможное количество положительных чисел равно 12
Ответ: наибольшее возможное количество положительных чисел равно
Заключение
Таким образом, на сегодняшний день актуальна проблема одновременного изучения школьного курса математики и элементов логики. Школьная математика – основа всей математики. Чтобы изучение шло успешно, необходимо усвоить азы. Для этого необходимо, прежде всего, научить решать задачи, особенно логические. Задачи, которые кажутся на первый взгляд простыми, могут потребовать остроумия, смекалки при ее решении. 