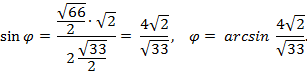При решении геометрических задач, как правило, алгоритмов нет, и выбрать наиболее подходящую к данному случаю теорему из большого количества теорем не просто. А ещё это связано с тем, что редко какая задача в геометрии может быть решена с использованием определенной формулы. При решении большинства задач не обойтись без привлечения разнообразных фактов теории, доказательства тех или иных утверждений, справедливых лишь при определенном расположении элементов фигур.

Особые затруднения вызывают стереометрические задачи, в которых требуется построить сечение многогранника плоскостью, найти площадь сечения, угол между скрещивающимися прямыми, угол между прямой и плоскостью, двугранные углы между плоскостями. Перечисленные задания в демонстрационном варианте ЕГЭ по математике составляют содержание задач уровня №14. Эта тема актуальна всем тем, кому предстоит сдавать профильный экзамен по математике. Согласно статистике, у большинства сдающих ЕГЭ по математике возникают трудности при решении стереометрических задач под №14. Материалом исследования послужили книга Э.Г. Готмана «Стереометрические задачи и методы их решения» и статья И.В. Яковлева «Метод объёмов».

В центре внимания исследовательской работы положен метод объёмов.

Объект исследования: стереометрические задачи, требующие нахождения расстояния между прямой и плоскостью; угла между прямой и плоскостью; угла между плоскостями; расстояния между скрещивающимися прямыми.

Предмет исследования: метод объёмов.

Гипотеза: метод объёмов в некоторых случаях позволяет получить результат, который при других способах решения получается гораздо сложнее.

Цель работы: изучение применения метода объёмов при решении стереометрических задач.

Задачи:

1. Проанализировать различные аспекты изучения данной темы. (Осуществить поиск и отбор информации о методе объёмов, изучить и доказать теоремы, позволяющие применять данный метод при решении стереометрических задач).

2. Проанализировать и выявить факты, подтверждающие возможность применение метода объёма при решении задач по математике на ЕГЭ.

3. Организовать сбор задач, из вариантов ЕГЭ по математике, при решении которых может применяться метод объёмов.

4. Научиться применять метод объёмов при решении стереометрических задач.

5. Оформить результаты исследования.

Результатом исследования должна стать презентация по теме, которая поможет выпускникам познакомиться с методом объёмов и покажет возможность применения этого метода для решения заданий №14 на ЕГЭ по математике и подборка задач из ЕГЭ по математике, при решении которых применялся метод объёмов. Подборка задач может быть применена и преподавателями математики в качестве раздаточного материала при подготовке к ЕГЭ.

Метод объёмов при решении стереометрических задач

При изучении литературы по теме «Решения стереометрических задач» можно встретить различную классификацию методов решений.

Существует три основных метода решения задач №14. Условно назовем их «методом построений», «векторно-координатным методом» и «методом объемов». Каждый из них удобен в том или ином случае, поэтому лучше знать и уметь использовать все три.

Объём треугольной пирамиды можно посчитать несколькими разными способами. Методом объёмов мы называем приравнивание двух подходящих выражений для объёма, в результате чего удаётся вычислить искомую величину (расстояние или угол). Метод объёмов можно использовать, вычисляя:

• расстояние от точки до плоскости;
• угол между прямой и плоскостью;
• угол между плоскостями;
• расстояние между скрещивающимися прямыми.

С идейной точки зрения метод объёмов весьма прост. Всё, что здесь нужно, — это найти подходящую треугольную пирамиду и аккуратно провести вычисления. Правда, вычислений обычно получается несколько больше, чем в методах, рассмотренных выше. Но тут уж ничего не поделаешь — за простоту метода приходится платить. [3,с.1]

1.1 Расстояние от точки до плоскости

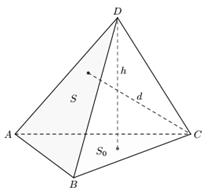
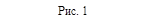
Треугольная пирамида замечательна тем, что для вычисления её объёма, за основание можно выбрать любую её грань. Этот факт можно использовать при нахождении расстояния от точки до плоскости; нужно лишь представить искомое расстояние как высоту подходящей пирамиды. Рассмотрим пример. Дана треугольная пирамида ABCD (рис.1). Нужно найти расстояние от некоторой точки С до некоторой плоскости ABD. Тогда искомое расстояние – это высота d данной пирамиды, проведённой из вершины C.

Пусть S0 – площадь грани ABC, h – высота, опущенная на эту грань, S – площадь грани АВД. С одной стороны, объём пирамиды ABCD может быть найден по формуле:

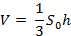(1)

С другой стороны, за основание можно принять грань ABD, и тогда

(2)

Приравниваем правые части формул (1) и (2), получаем:

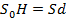(3)

Из соотношения (3) находим искомую величину d.Пример решения стереометрической задачи на нахождение расстояния от точки до плоскости приведён в приложении № 2.Метод объёмов позволяет найти высоту без построения перпендикуляра, опущенного из точки на плоскость. Освоив столь мощный метод нахождения расстояния от точки до плоскости, мы в качестве «дополнительной опции» немедленно получаем метод вычисления угла между прямой и плоскостью [7, с.3].

1.2 Угол между прямой и плоскостью

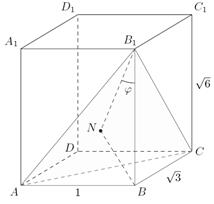
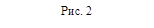
ABCDA1B1C1D1 (рис 2) известны рёбра: AB = 1, AD= 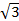, AA1 = 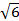. Найдите угол между прямой BB1 в прямоугольном параллелепипеде и плоскостью AB1C.

Искомый угол φ.

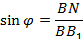  (4)

где BN – расстояние от точки В до плоскости АВ1С находим методом объёмов по формуле:

.

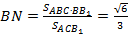Далее подставляем полученный результат в формулу (4).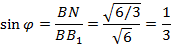

Ответ: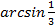

1.3 Угол между плоскостями

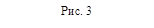
При вычислении угла между плоскостями может оказаться полезной следующая формула для объёма треугольной пирамиды:

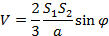 (5)

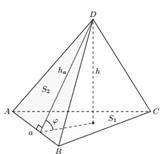
Здесь S1 и S2 - площади двух граней пирамиды, a- общее ребро этих граней, 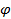- угол между плоскостями этих граней (рис 3).

Рассмотрим вывод формулы (5). Пусть S1 и S2 - площади треугольников ABC и ABD соответственно, a= AB, 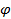- угол между плоскостями ABC и ABD.

Из вершины D проведём высоту пирамиды h и высоту грани h_a грани ABD. Легко видеть, что 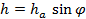. Тогда для объёма пирамиды имеем:

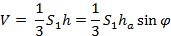(6)

С другой стороны, запишем формулу для площади S2:

,

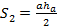Откуда

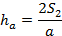
Это выражение нужно подставить в (6):

.

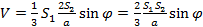Что и нужно было получить.

Рассмотрим решение задачи:

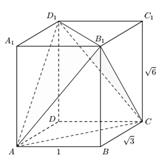
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра: AB = 1, 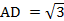, 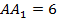. Найдите угол между плоскостями AB1D1 и CB1D1. Решение. Делаем чертёж (рис. 4). Искомый угол Φ будем вычислять с помощью треугольной пирамиды AB1CD1.

Согласно формуле (5) имеем:

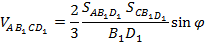 (7)

Объём тетраэдра AB1CD1 мы найдём, «отрезая» от исходного параллелепипеда четыре равнообъёмных «куска»:

.

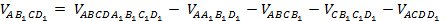Следовательно,

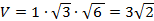
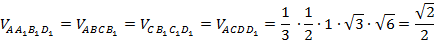
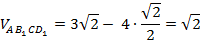
Теперь найдём площади граней AB1D1 и CB1D1. Имеем:

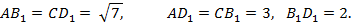
Таким образом, треугольники AB1D1 и CB1D1 имеют стороны 2,3 и .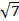

Находим их площадь по формуле Герона. Получаем:

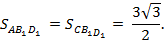
Подставляем найденные величины в формулу (7):

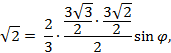
откуда

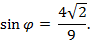
Ответ: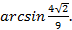

1.2 Расстояние между скрещивающимися прямыми

При нахождении расстояния между скрещивающимися прямыми может помочь следующая формула для объёма тетраэдра:

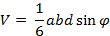 (8)

Здесь a и b – скрещивающиеся рёбра тетраэдра, d и 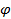- соответственно расстояние, и угол между ними (точнее, между прямыми, содержащими эти рёбра).

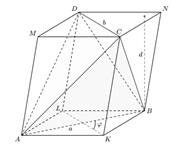
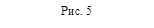
Дадим вывод этой формулы.

На рисунке мы видим тетраэдр ABCD, достроенный до параллелепипеда AKBLMCND следующим образом: через каждое ребро тетраэдра проведена плоскость, параллельная ребру, скрещивающемуся с данным ребром. Покажем, что объём V тетраэдра ABCD равен одной третьи объёма V0 получившегося параллелепипеда.

Отрезаем от параллелепипеда четыре тетраэдра:

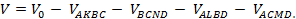
Все эти тетраэдры имеют одинаковый объём. В самом деле, если S и d – соответственно площадь основания и высота параллелепипеда, то

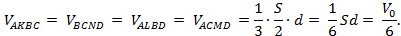
Тогда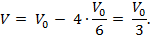

Пусть a = AB, b = CD. Расстояние между прямыми, проходящими через рёбра a и b, являются расстоянием между параллельными плоскостями AKB и MCN, то есть высотой d нашего параллелепипеда. Угол между рёбрами a и b – это угол 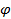между прямыми AB и KL.

Для площади основания параллелепипеда имеем:

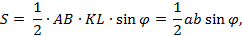
Находим объём параллелепипеда:

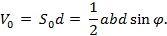
Объём тетраэдра ABCD меньше в три раза, тем самым, получаем нужную формулу (8).Применение данной формулы и метода объёмов рассмотрено на примере решения задачи «В кубе ABCDA1B1C1D1 найдите расстояние между прямыми A1B и B1C. Ребро куба равно 3.» представлено в приложении № 2.

Метод объёмов помог, не производя построений, найти расстояние между скрещивающими прямыми. Что значительно облегчает решение задачи.

Решение стереометрических задач из ЕГЭ по математике методом объемов

Содержание и структура экзаменационной работы дают возможность проверить усвоение курсов математики 5—6-го классов, алгебры 7—9-го классов, алгебры и начал анализа 10-11-го классов и геометрии 7—11-го классов. При этом, в частности, проверяются умения использовать полученные знания в практической деятельности и в повседневной жизни, а также умения строить и исследовать математические модели.Задача №14. Стереометрия. Построение сечения. Нахождение каких-либо величин через заданные [6, с.2].

2.1. Характеристика стереометрических задач №14 из ЕГЭ по математике

В задаче 14 рассматриваются многогранники, на основе которых, как правило, нужно найти одну из следующих величин:

1. Угол между скрещивающимися прямыми — это угол между двумя прямыми, которые пересекаются в одной точке и параллельны данным прямым.

2. Угол между прямой и плоскостью — это угол между самой прямой и ее проекцией на данную плоскость.

3. Угол между двумя плоскостями — это угол между прямыми, которые лежат в данных плоскостях и перпендикулярны линии пересечения этих плоскостей. [6, с.5]

Прямые всегда задаются двумя точками на поверхности или внутри многогранника, а плоскости — тремя. Сами многогранники всегда задаются длинами своих граней.

В школьном курсе стереометрии упор делается на дополнительные построения, которые позволяют выделить искомый угол, а затем рассчитать его величину.

Здесь уместно вспомнить задачи на построение сечений многогранников, которые рассматриваются в 10 классе и у многих вызывают трудности. Существование формального алгоритма для таких построений совершенно не облегчает задачу, поскольку каждый случай достаточно уникален, а любая систематизация лишь усложняют процесс.

Именно поэтому задача 14 оценивается в два балла. Первый балл дается за правильные построения, а второй — за правильные вычисления и собственно ответ.

Преимущества традиционного решения:

1. Высокая наглядность дополнительных построений, которые подробно изучаются на уроках геометрии в 10-11 классах;

2. При правильном подходе значительно сокращается объем вычислений.

Недостатки:

1. Необходимо знать большое количество формул из стереометрии и планиметрии;

2. Дополнительные построения каждый раз приходится придумывать «с нуля». И это может оказаться серьезной проблемой даже для хорошо подготовленных учеников.

Вот в таких трудных случаях, когда «метод построений» не даёт нужного результата, на помощь приходят два метода - это «векторно-координатным метод» и «методом объемов».

2.2. Решение задач №14 из ЕГЭ по математике

Покажем применение метода объёмов при решении стереометрических задач из ЕГЭ по математике.На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA =1: 2 , на ребре BB1 — точка F так, что B1F : FB =1:5 , а точка T — середина ребра B1C1 . Известно, что AB = 4, AD = 2, AA1 = 6.

а) Докажите, что плоскость EFT проходит через вершину D1.

б) Найдите угол между плоскостью EFT и плоскостью BB1C1

Доказательство приведено в приложении № 3.

Рассмотрим нахождение угла между плоскостью EFT и плоскостью BB1C1. Обозначим искомый угол между плоскостями через 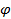. Рассмотрим треугольную пирамиду EFTC. Вычислим объём этой пирамиды двумя способам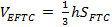и:

и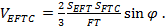

И уравняв правые части, выразим 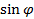, получим формулу:

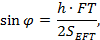
где h – высота пирамиды, опущенная из вершины E. Полное решение приведено в приложении № 3.

Вывод: при использовании метода объёмов получили много вычислений, но преимущество данного метода в отсутствии построения угла между плоскостями. На практике такое построение часто вызывает затруднения.

Заключение

В ходе исследования был изучен метод объёмов при решении стереометрических задач и сделан вывод: метод объёмов в некоторых случаях позволяет получить результат, который при других способах решения получается гораздо сложнее.

Таким образом, гипотеза подтвердилась.В заключение следует отметить, что выведенные, в ходе исследования, формулы

,

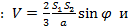
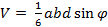значительно обогатят багаж математических знаний, обучающихся 11 класса и расширят возможности в нахождении способов решения стереометрических задач, а по мнению Р.К. Гордина эти формулы входят в перечень основных знаний по стереометрии. [1, с. 23]

Задачи по стереометрии — прекрасные упражнения, способствующие развитию пространственных представлений, умения логически мыслить, способствующие развитию творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности.

Приложение 1

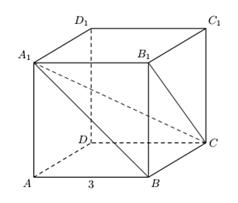
В кубе ABCDA1B1C1D1 найдите расстояние между прямыми A1B и B1C. Ребро куба равно 3.

Объём V данного тетраэдра легко найти, приняв за основание грань BCB1. Тогда:

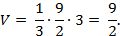
С другой стороны, согласно формуле (8) имеем:

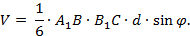
Здесь

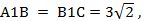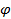угол между прямыми A1B и B1C равен 600, так что имеем:

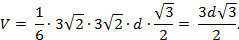
Остаётся приравнять выражения для объёма и найти требуемое расстояние: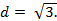

Приложение 2

Задача№14 из вариант МА10107 (профильный) Математика. 11 класс, ноябрь 2015 года.На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA =1: 2 , на ребре BB1 — точка F так, что B1F : FB =1:5 , а точка T — середина ребра B1C1 . Известно, что AB = 4, AD = 2, AA1 = 6.

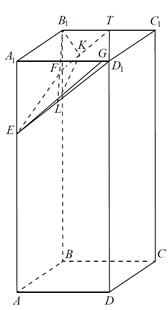
а) Докажите, что плоскость EFT проходит через вершину D1.

Решение: a) В плоскости AA1D1 проведём через точку E прямую, параллельную TF. Пусть она пересекает ребро AD1 или его продолжение точке G . Плоскость EFT проходит через точку G . Треугольник EGA1 подобен равнобедренному треугольнику FTB1 , в котором FB1 = B1T =1. Отсюда EA1 = A1G = 2 , значит, точка G совпадает с точкой D1 .

б) Найдите угол между плоскостью EFT и плоскостью BB1C1

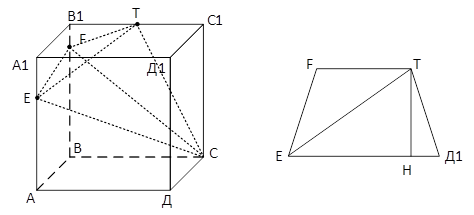
б) Обозначим искомый угол между плоскостями через 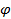. Рассмотрим треугольную пирамиду EFTC. Вычислим объём этой пирамиды двумя способам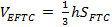и:

и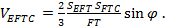

И уравняв правые части, выразим 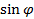, получим формулу:

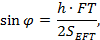
где h – высота пирамиды, опущенная из вершины E. FT находим из прямоугольного треугольника FB1T, 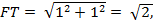а площадь треугольника EFT по формуле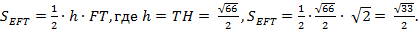

Имеем: