В массовом сознании сформировалось представление о математике как о сухой науке, в которой нет места красоте, присущей, например, искусству. При этом почти каждый слышал, что математика – образец элегантности и гармонии. Так с чем связано возникновение совершенно противоположных взглядов относительно красоты этой науки? Все дело в правильном взгляде на математику! Насладиться ее красотой непросто, потому что для этого необходимо видеть структуру идей, из которых состоит рассуждение, а также уметь оценивать гармоничность их сочетания. Красота математики доступна только тем, кто обладает развитой способностью чувствовать эстетичность математических рассуждений. Но ведь красоту поэзии также невозможно оценить с помощью органов чувств. Для осознания эстетической ценности поэзии необходим определенный анализ. Ее красота также неосязаема и требует интенсивной работы разума для возможности ее восприятия. Именно в этом и заключается взаимосвязь математики и поэзии, которая находит применение в изучении науки.
Так, теоремы геометрии, представленные в стихотворной форме, демонстрируют гармоническую целостность эстетики математических рассуждений и звучания отдельных слов.
|
Синуса острого угла нахождение – Противолежащего катета к гипотенузе отношение. |
(1) |
|
Чтобы косинус острого угла получить – Нужно прилежащий катет на гипотенузу поделить. |
(2)
|
|
Найти тангенс можно всегда, Поделив синус на косинус угла. |
(3)
|
Примечание
Для того чтобы запоминание подобных мнемонических правил было эффективным, учащимся необходимо обращать внимание на их фонетическую организацию. Так, в правиле №2 после слова «чтобы» идет слово «косинус», также имеющее в составе звук О. Запомнив эту закономерность, ученик не подставит вместо слова «косинус» слово «синус». Также необходимо заметить, что последнее слово в первых двух правилах служит подсказкой в запоминании катетов: прилежащий (противолежащий) катет – поделить (отношение). К тому же эти мнемонические правила представляют собой совершенно разные синтаксические конструкции, поэтому ученик не совершит ошибку при их применении, если обратит внимание на эти замечания.
|
Если катет лежит против 30-тиградусного угла, То половине гипотенузы равна его величина.
|
(4) |
|
Площадь любой трапеции найти – не беда: Произведение суммы оснований и высоты делить на 2. |
(5) |
|
Площади ромба получение – Деленное на 2 диагоналей произведение.
|
(6) |
|
Параллелограмма площадь найти легко, Умножив сторону на высоту, опущенную на нее.
|
(7) |
|
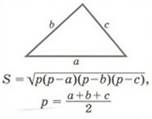
В первом веке жил Герон, Формулу придумал он. Из полусуммы всех сторон Их длины поочередно вычел он. И знает каждый с тех времен: Под корнем р на р без соответствующих сторон.
|
(8)
|
Многие школьники испытывают трудности при изучении геометрии, поэтому подобные стихотворения способны не только указать на неизбежную связь математики и поэзии, продемонстрировав их эстетическую ценность, но и значительно облегчить процесс запоминания геометрических теорем и формул. Ведь созвучность определенных слов, представленных в стихотворной форме, делает акцент на отдельных элементах математических рассуждений, ключевых для понимания теоремы. Подобный подход, основанный на применении взаимосвязи математики и поэзии, делает изучение математики увлекательнее и понятнее.