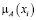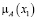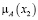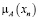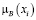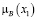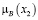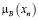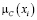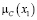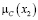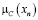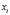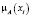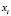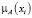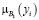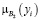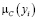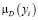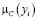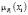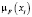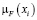Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте VII Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://school-science.ru/7/7/39442.
Исследования на тему «Нечёткие множества учеников нашего класса» для нас интересны и актуальны.
На уроках математики мы познакомились с множеством натуральных чисел, которое используют для счёта предметов, множеством целых чисел и множеством рациональных чисел. Какие ещё множества чисел существуют? – возник у нас вопрос. В сети Internet кроме определений разных числовых множеств, мы нашли определение и примеры нечётких множеств. Оказалось, что с помощью нечётких множеств можно описывать различные явления, свойства и качества объектов, а также работать с ними, как с числами в математике (складывать, вычитать, умножать и делить). А ещё мы выяснили, что нечёткие множества – это основные элементы нечёткой логики и нечёткого управления, которые изучаются студентами специальностей, связанных с математическим моделированием.
Нам стало интересно, сможем ли мы разобраться с понятием «нечёткое множество», построить некоторые множества на примере учеников нашего класса и выполнить несложные логические операции над ними.
В настоящей научно-исследовательской работе мы сделали попытку с помощью нашего руководителя изучить понятие «нечёткое множество» и его построение на основе экспертных оценок.
Любому, читающему нашу работу будет интересно узнать, что кроме традиционного понятия множества, есть и понятие – «нечёткое множество», которое является более широким и более универсальным для описания различных явлений и объектов. Мы сделаем свои первые шаги к изучению математического понятия «нечёткое множество», построим несколько нечётких множеств для описания учеников нашего класса и выполним некоторые логические операции с ними.
Гипотеза исследования: нечёткое множество является более широким понятием, чем обычное множество, оно может быть построено нами самостоятельно с применением экспертных оценок и являться основой для построение других нечётких множеств с помощью логических операций.
Цель исследования – создание своих нечётких множеств для описания учеников нашего класса, а также построение с помощью логических операций других нечётких множеств и нечёткого отношения.
Задачи исследования:
1) Изучить понятие «нечёткое множество» и историю его возникновения, изучить способы описания нечётких множеств, привести примеры.
2) Познакомиться с методами экспертных оценок для построения нечётких множеств: метод привлечения равноправных экспертов и метод упорядочивания последовательности принимаемых решений.
3) Познакомиться с некоторыми операциями над нечёткими множествами: логические операции «И», «ИЛИ», «НЕ» и понять, что такое нечёткое отношение.
4) Разработать анкеты и провести опрос среди учеников нашего класса для получения исходных данных (экспертных оценок) для построения нечётких множеств.
5) Самостоятельно построить нечёткие множества учеников нашего класса.
Объект исследования – нечёткие множества.
Предмет исследования: способы построения нечётких множеств.
Методы исследования: изучение литературы и Интернет-ресурсов, беседа со специалистом, извлечение знаний, систематизация информации и анализ, моделирование подобных объектов на основе полученных знаний.
Ожидаемые результаты исследования:
• получение новых знаний в области математики и информатики;
• применение полученных знаний для создания новых объектов;
• разработанные нечёткие множества.
Выполненная работа позволила нам получить новые знания по математике (обработка статистических данных в виде экспертных оценок, построение точечных графиков функций и работа с ними), применить их на практике и получить результат. В области информатики мы получили новые знания работая в приложении Excel Microsoft Office 2016 для оформления результатов научно-исследовательской работы.
Настоящая научно-исследовательская работа демонстрирует то, что нечёткие множества можно создать для описания различных объектов, например, для описания множества учеников нашего класса, а также, что подобные нечёткие множества можно разработать самостоятельно, так же, как сделали мы – авторы работы.
1. Понятие «нечёткое множество» в примерах
Автором термина «нечёткое множество» является американский математик Лотфи Заде (см. Приложение А). Название «нечёткое множество» произошло после перевода на русский язык статьи Л. Заде «Fuzzy sets» (1965г.). Слово fuzzy переводится как нечёткое (или размытое, расплывчатое, туманное, пушистое), а слово set – множество.
Понятие «нечёткое множество» мы объясним на простых примерах.
Пример №1. Софизм «Куча»
Софизмы – это ошибки в суждениях, которые совершаются намеренно. Софизм всегда содержит одну или несколько замаскированных ошибок.
Знаменитый софизм «Куча» обсуждали ещё древнегреческие философы.
«Одно зерно не составляет кучи, не составляют её и два, и три, … С другой стороны, каждый согласится, что сто миллионов зёрен образует кучу. Какова же точная грань? Можно ли допустить, что 325 647 зёрен не образует кучи, а 325 648 зёрен её образуют?» [2].
Может быть и такая формулировка: «Одно зерно – не куча. Если к тому, что не составляет кучи, добавить одно зерно, то куча не получится. Следовательно, никакое количество зёрен не составляет кучу». Утверждение явно неверное.
Пусть проводится опрос нескольких людей, которым предлагаются наборы из х зёрен и людей спрашивают: «Это куча?». При маленьком n все одинаково считают, что это «не куча». При многих миллионах – это «куча». При промежуточных значениях х мнения разделяются. В результате получается нечёткое множество мнений – «куча – не куча».
Если принадлежность мнения к мнению «куча» обозначить за 1, а принадлежность к мнению «не куча» за 0, то промежуточные мнения будут иметь принадлежность от 0 до 1. Если множество мнений обычное, то может быть только два варианта: «куча» – 1 или «не куча» – 0. Если множество мнений нечёткое, то возможные несколько вариантов, например, «скорее куча, чем нет» – 0,8; «похоже на кучу» – 0,6; «наверно, не куча» – 0,3.
Числовые значения 0; 0,3; 0,6; 0,8; 1 – значения функции принадлежности мнения эксперта к понятию «куча». Пусть х – количество зёрен, тогда µ(х) – функция принадлежности к понятию «куча».
Мы решили сами высказать своё мнение и построить нечёткое множество. В табл. 1, 2 приведено нечёткое множество мнений по понятию «куча» Первушина В. (табл. 1) и Пермякова Е. (табл. 2).
Таблица 1
Мнение Первушина В.
|
х1 – количество зёрен |
5 |
100 |
200 |
450 |
500 |
|
µ(х1) – принадлежность к мнению «куча» |
0 |
0,3 |
0,6 |
0,8 |
1 |
Таблица 2
Мнение Пермякова Е.
|
х2 – количество зёрен |
10 |
20 |
500 |
800 |
1000 |
|
µ(х2) – принадлежность к мнению «куча» |
0 |
0,3 |
0,6 |
0,8 |
1 |
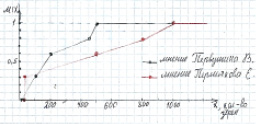
Рис. 1
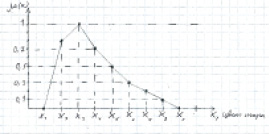
Рис. 2
Пример №2. Шары красного цвета
Пусть имеется набор шаров различных оттенков красного цвета. Требуется описать нечёткое множество – «шар красного цвета». Мы построили нечёткое множество по образцу, приведённому в примере №1, а также обычное множество. Результаты построения приведены в табл. 3.
Таблица 3
Нечёткое и обычное множество «Шары красного цвета»
|
х – шар красного оттенка |
|||||||||
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
х9 |
|
|
µ(х) – принадлежность к понятию «красный шар» |
0 |
0,8 |
1 |
0,7 |
0,5 |
0,3 |
0,2 |
0,1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
На рис. 2 нечёткое множество шаров красного цвета представлено графически.
Далее будут представлены два способа построения нечётких множеств с применением экспертных оценок. Построение нечёткого множества называется – фаззификация.
2. Методы экспертных оценок для построения нечётких множеств
2.1. Метод привлечения равноправных экспертов
Пусть имеется явление A, которое может принимать одно из значений х1, х2, …, хn [3]. Например, явление А – прибор. Оценивается уровень качества его работы: х1 – работает хорошо, х2 – работает очень хорошо, х3 – работает довольно хорошо, х4 – работает довольно плохо, х5 – не работает.
Для принятия решения о работоспособности прибора привлекается группа из N равноправных экспертов, каждый из которых имеет n голосов для оценки значений хi. Эксперт, оценивая явление А, отдаёт или не отдаёт свой голос за хi. Голос может быть отдан сразу нескольким хi.
Обозначим K – максимальное количество голосов за хi (обычно совпадает с числом экспертов N), Ki – количество голосов, отданное за хi. Тогда значения функции принадлежности к нечёткому множеству вычисляются так:
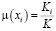 . (1)
. (1)
Значение (1) равно 1, если Ki = K, т.е. значение хi получило максимальное количество голосов. Значение (1) равно 0, если Ki = 0, т.е. значение хi не получило ни одного голоса от экспертов.
2.2. Метод упорядочивания последовательности принимаемых решений
Пусть имеется явление A, которое может принимать одно из значений х1, х2, …, хn. Эксперт расставляет эти значения в порядке предпочтения – от «худшего» к «лучшему» [3]. Степень предпочтения предложено оценивать значениями от 0 до 1: «гораздо больше» – 1; «больше» – 0,75; «чуть больше» – 0,5; «больше или равно» – 0,25; «равноценны» – 0.
Например, явление А может принимать значения {х1, х2, х3, х4, х5}. Эксперт расставил эти значения в порядке предпочтения:
х4 0,75 х1 0,5 х3 0 х2 0,75 х5
Расстояние между любыми элементами – это сумма числовых значений между ними. Определим расстояние от худшего элемента х4 до всех остальных:
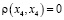 ;
; 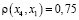 ;
;
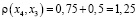 ;
;
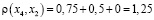 ;
;
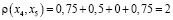 .
.
Максимально возможное расстояние на один меньше числа элементов в цепочке предпочтений 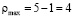 , т.к. максимальная степень предпочтения «гораздо больше» соответствует числу 1, а сравниваемых элементов 5.
, т.к. максимальная степень предпочтения «гораздо больше» соответствует числу 1, а сравниваемых элементов 5.
Значения функции принадлежности к нечёткому множеству вычисляются так:
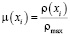 . (2)
. (2)
Значения, полученные по формулам (1) и (2) меньше 1, если все голоса не отданы за одно значение хi.
3. Операции над нечёткими множествами
Пусть даны два нечётких множества A и В, заданные таблицей на одном и том же наборе значений х1, х2, …, хn. Результат операции – нечёткое множество С [4].
Таблица 4
|
хi |
х1 |
х2 |
… |
хn |
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
Пересечение нечётких множеств (логическое «И»)
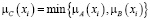 . (3)
. (3)
Объединение нечётких множеств (логическое «ИЛИ»)
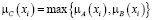 . (4)
. (4)
Дополнение к нечёткому множеству (логическое «НЕ»)
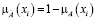 . (5)
. (5)
4. Результат построения нечётких множеств учеников нашего класса
4.1. Экспертные оценки
Для построения нечётких множеств учеников нашего 6В класса мы решили разработать опросные листы, чтобы экспертами были сами учащиеся.
Мы выбрали такие характеристики наших одноклассников (мальчиков и девочек) для построения нечётких множеств, как: 1) весёлый/весёлая; 2) спортивный/спортивная; 3) модный/модная; 4) дружелюбный/дружелюбная; 5) активный/активная.
В соответствии с этими характеристиками был разработан опросный лист (анкета), который заполнил каждый ученик нашего класса, присутствовавший на момент опроса в школе. Всего было заполнено 24 анкеты, образец которой приведён на рис. Б.1 Приложения Б.
Каждый из участников опроса должен был отметить по 3 человека, соответствующих указанной характеристике. В результате были получены экспертные оценки. Все анкеты были обработаны с помощью офисного приложения Excel, а затем методами п. 2.1 и п. 2.2 построены нечёткие множества.
Пример подсчёта голосов экспертов для построения нечёткого множества «весёлый мальчик» приведён в Приложении Б на рисунке Б.2. Таким же способом были получены суммарные голоса по всем характеристикам, указанным в опросном листе.
Суммарные экспертные оценки показаны в таблицах Б.1 и Б.2 Приложения Б.
4.2. Построение нечётких множеств методом привлечения равноправных экспертов
Для примера, построим нечёткое множество A – «модная девочка». Исходные данные для построения мы взяли в Таблице Б.1 Приложения Б. В соответствии с методом п. 2.1, обозначим множество значений явления A (множество девочек) как: х1, х2, х3, х4, х5, х6, х7, х8, х9, х10, х11, х12, х13, х14. Всего экспертов (учеников) – 24. В формуле (1) К=24.
В табл. 5 все значения получились меньше 1. Нечёткое множество нужно нормализовать, т.е. преобразовать так, чтобы максимальное значение 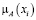 было равно 1. Это можно сделать, например, разделив каждое значение
было равно 1. Это можно сделать, например, разделив каждое значение 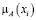 в табл. 5 на максимальное значение
в табл. 5 на максимальное значение
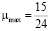 .
.
График функции принадлежности нечёткого множества А построен по данным табл. 6 показан на рис. 3.
Таблица 5

Таблица 6

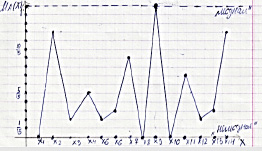
Рис. 3. Нечёткое множество A – «модная девочка»
Нечёткое множество «модная девочка» построено. Остальные нечёткие множества построены с помощью офисного приложения Excel. Таблица значений приведена в Приложении В, а графики в Приложении Г на рис. Г.1 – для девочек, а на рис. Г.2 – для мальчиков.
4.3. Построение нечётких множеств методом упорядочивания последовательности принимаемых решений
Рассмотрим также для примера нечёткое множество A – «модная девочка». Далее, в зависимости от количества голосов, отданных за девочек, расставим их в порядке: от меньшего количества к большему.
Таблица 8


Рис. 4
В соответствии с методом п. 2.2, обозначим множество девочек как: х1, х2, х3, х4, х5, х6, х7, х8, х9, х10, х11, х12, х13, х14. Степень предпочтения одного варианта перед другим обозначим числами 0; 0,25; 0,5; 0,75 и 1.
Мы решили по такому правилу расставлять предпочтения: если разница в числе голосов в 1, то 0,25; если разница в 2 голоса, то 0,5; если разница в 3 голоса – 0,75; если разница в 4 голоса и более, то 1. По данным таблицы 8 получилась цепочка предпочтений – рис. 4. Далее мы определили расстояния от худшего варианта до всех остальных.
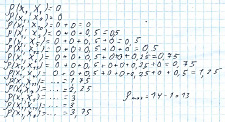
Рис. 5
По формуле (2) вычисляем значения функции принадлежности к нечёткому множеству А – «модная девочка». Результат вычисления приведён в табл. 9.
Таблица 9
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
х9 |
х10 |
х11 |
х12 |
х13 |
х14 |
|
|
0 |
0,23 |
0,04 |
0,1 |
0,04 |
0,06 |
0,17 |
0 |
0,29 |
0 |
0,13 |
0,04 |
0,06 |
0,23 |
В табл. 9 все значения получились меньше 1. Нечёткое множество нужно нормализовать, как в предыдущем методе.
Разделим каждое 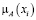 в табл. 9 на максимальное значение
в табл. 9 на максимальное значение 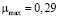 .
.
Таблица 10
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
х9 |
х10 |
х11 |
х12 |
х13 |
х14 |
|
|
0 |
0,8 |
0,13 |
0,33 |
0,13 |
0,2 |
0,6 |
0 |
1 |
0 |
0,47 |
0,13 |
0,2 |
0,8 |
График функции принадлежности нечёткого множества А построен по данным таблицы 13 на рис. 6.
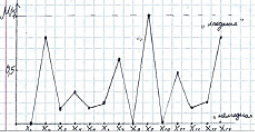
Рис. 6. Нечёткое множество A – «модная девочка»
Остальные нечёткие множества построены с помощью офисного приложения Excel. Таблица значений приведена в Приложении Д, а графики в Приложении Е на рис. Е.1 – для девочек, а на рис. Е.2 – для мальчиков.
4.4. Выводы по методам построения нечётких множеств
На рис. 3 и 6 приведены графики нечёткого множества A – «модная девочка». На рис. 3 – результат получен методом привлечения равноправных экспертов, а на рис. 6 – методом упорядочивания последовательности принимаемых решений. Графики одинаковые по характеру расположения точек. Это свидетельствует о том, что нечёткое множество построено верно. Для построения может применяться любой из описанных методов.
На основе полученного нечёткого множества можно сделать вывод: все девочки нашего класса модные, но степень принадлежности к понятию «модная» у всех разная. Самые модные девочки, у которых степень принадлежности к понятию «модная» от 0,5 до 1 это – Анастасия Б., Дарья К., Мария Л. и Вероника Ш. Аналогичные выводы можно построить на основе остальных результатов, приведённых в Приложениях В – Е.
4.5. Построение нечётких множеств «весёлый И дружелюбный мальчик» и «весёлый ИЛИ дружелюбный мальчик»
С нечёткими множествами можно выполнять различные операции. Логическая операция «И» – формула (3) применяется при построении, например, нечёткого множества С – «весёлый и дружелюбный мальчик». Логическая операция «ИЛИ» – формула (4) применяется при построении, например, нечёткого множества D – «весёлый или дружелюбный мальчик».
Исходные данные возьмём из таблицы приложения В: нечёткое множество В1 – «весёлый мальчик» и нечёткое множество В2 – «дружелюбный мальчик».
Таблица 11
|
yi |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y9 |
y10 |
y11 |
y12 |
y13 |
|
|
0,46 |
0,54 |
0,23 |
0,08 |
0,15 |
0,69 |
0,54 |
0,31 |
1 |
0,62 |
0,31 |
0,23 |
0,38 |
|
|
0,7 |
1 |
0,3 |
0,2 |
0,9 |
0,1 |
0,6 |
0,3 |
0,7 |
0,9 |
0,5 |
0,6 |
0,4 |
|
|
0,46 |
0,54 |
0,23 |
0,08 |
0,15 |
0,69 |
0,54 |
0,3 |
0,7 |
0,62 |
0,31 |
0,23 |
0,38 |
|
|
0,7 |
1 |
0,3 |
0,2 |
0,9 |
0,69 |
0,6 |
0,31 |
1 |
0,9 |
0,5 |
0,6 |
0,4 |
Таблица 12
|
yi |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y9 |
y10 |
y11 |
y12 |
y13 |
|
|
0,66 |
0,77 |
0,33 |
0,11 |
0,22 |
0,14 |
0,77 |
0,43 |
1 |
0,88 |
0,44 |
0,33 |
0,55 |
В табл. 11 значения 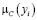 получились меньше 1. Разделим каждое значение
получились меньше 1. Разделим каждое значение 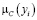 на максимальное значение
на максимальное значение 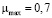 .
.
Построенные нечёткие множества показаны на рис. Ж.1 Приложения Ж.
Самые весёлые и дружелюбные мальчики, у которых степень принадлежности к понятию «весёлый и дружелюбный» от 0,5 до 1 это – Богдан Б., Никита Д., Артём К., Владимир П., Егор П., Кирилл Ю.
Самые весёлые или дружелюбные мальчики, у которых степень принадлежности к понятию «весёлый или дружелюбный» от 0,5 до 1 это – Богдан Б., Никита Д., Богдан И., Алексей К., Артём К., Владимир П., Егор П., Александр П., Георгий Ч.
4.6. Построение нечёткого множества «Невесёлая девочка»
При построении нечёткого множества F – «невесёлая девочка» применяется логическая операция «НЕ» – формула (5).
Исходные данные возьмём из таблицы Приложения В.
В табл. 13 все значения получились меньше 1. Разделим каждое значение 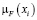 на максимальное
на максимальное 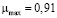 .
.
График нечёткого множества F – «невесёлая девочка» показан в Приложении Ж на рисунке Ж.1. Самые невесёлые девочки, у которых степень принадлежности к понятию «невеселая» от 0,5 до 1 это – Анастасия Б., Виктория В., Ариана И., Дарья Каз., Дарья Кор., Мария Л., Марина М., Елизавета Ф. и Вероника Ш.
Таблица 13
|
xi |
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
х9 |
х10 |
х11 |
х12 |
х13 |
х14 |
|
|
0,82 |
0,36 |
0,36 |
0,73 |
0,45 |
0,27 |
0,45 |
1 |
0,36 |
0,27 |
0,73 |
0,09 |
0,36 |
0,27 |
|
|
0,18 |
0,64 |
0,64 |
0,27 |
0,55 |
0,73 |
0,55 |
0 |
0,64 |
0,73 |
0,27 |
0,91 |
0,64 |
0,73 |
Таблица 14
|
xi |
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
х9 |
х10 |
х11 |
х12 |
х13 |
х14 |
|
|
0,2 |
0,7 |
0,7 |
0,3 |
0,6 |
0,8 |
0,6 |
0 |
0,7 |
0,8 |
0,3 |
1 |
0,7 |
0,8 |
4.7. Построение нечёткого отношения «быть парой – модная девочка и активный мальчик»
Самый простой вид отношения в математике – бинарное отношение, т.е. между двумя элементами множества. Примером являются отношения сравнения >, < или = .
Существуют бинарные нечёткие отношения. Например, R – «быть парой – модная девочка и активный мальчик». Нечёткое отношение – это тоже нечёткое множество, элементами которого являются пары значений. Степень выполнения отношения в данной паре определяется, например, через операцию min:
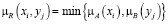 . (6)
. (6)
Описывать бинарные отношения удобно таблицей, элементы которой вычисляются по формуле (6). Пример построения нечёткого отношения R – «быть парой – модная девочка и активный мальчик» по данным Приложения В приведён в Приложении З. В таблице отмечены оранжевым цветом пары, для которых отношение выполняется со степенью 0,5 и более. Таких пар много. Например: 1) Мария Л., Владимир П.; 2) Кирилл Ю., Вероника Ш.; 3) Алексей К., Анастасия Б. и др.
4.8. Выводы по применению операций над нечёткими множествами
Операции над нечёткими множествами позволяют более точно описать явление или объект, а также, учесть несколько характеристик одновременно.
Заключение
В ходе научно-исследовательской работы выполнены все поставленные задачи.
По завершению научно-исследовательской работы мы подтвердили гипотезу о том, что нечёткое множество является более широким понятием, чем обычное множество, оно может быть построено нами самостоятельно с применением экспертных оценок и являться основой для построение других нечётких множеств с помощью логических операций.
Проведённое исследование позволило нам получить новые знания по математике и информатике, которые необходимо углублять, чтобы иметь возможность использовать нечёткие множества для решения важных задач в различных областях науки, связанных с применением методов нечёткого моделирования, как это делал Лотфи Заде и как это делают современные специалисты в области прикладной математики.
Текст работы был проверен в сервисе «Антиплагиат» http://users/antiplagiat.ru. Результат – 96 % оригинального текста и 4 % – заимствования (см. Приложение И).
Приложение А

Лотфи Заде, почётный профессор Калифорнийского университета в Беркли родился в Баку, Азербайджан, родился 4 февраля 1921 г., умер в Беркли, Калифорния, США 6 сентября 2017 г. (96 лет)
Лотфи Заде – автор термина «нечёткое множество», американский математик, основатель теории нечётких множеств и нечёткой логики, профессор Калифорнийского университета США [1].
Л. Заде опубликовал основополагающую работу по теории нечётких множеств «Fuzzy sets» в 1965 году в журнале «Information and Control», в которой изложил математический аппарат теории нечётких множеств.
Эта, имеющая историческое значение, работа определила новое научное направление, которое привело к огромному количеству публикаций в этой области с быстро растущим числом приложений, например, таких, как поезд метро и системы поддержки принятия решений. В настоящие годы влияние теории нечетких множеств, или «нечеткой логики», ощущается в области всех основных наук, особенно в математике, физике и химии.
Приложение Б (обязательное)
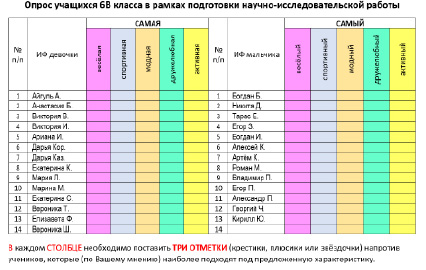
Рис. Б.1. Образец опросного листа
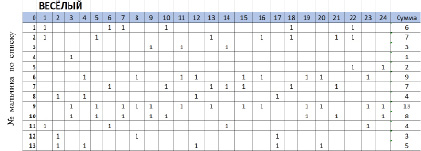
Рис. Б.2. Пример подсчёта голосов экспертов в Excel
Таблица Б.1
Экспертные оценки по характеристикам девочек
|
№ девочки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
1) Весёлая |
9 |
4 |
4 |
8 |
5 |
3 |
5 |
11 |
4 |
3 |
8 |
1 |
4 |
3 |
|
2) Спортивная |
1 |
11 |
17 |
2 |
9 |
2 |
1 |
3 |
2 |
1 |
15 |
1 |
5 |
2 |
|
3) Модная |
0 |
12 |
2 |
5 |
2 |
3 |
9 |
0 |
15 |
0 |
7 |
2 |
3 |
12 |
|
4) Дружелюбная |
9 |
3 |
4 |
6 |
9 |
5 |
0 |
5 |
6 |
6 |
5 |
4 |
3 |
7 |
|
5) Активная |
7 |
2 |
7 |
4 |
4 |
2 |
4 |
11 |
5 |
4 |
9 |
2 |
5 |
6 |
Таблица Б.2
Экспертные оценки по характеристикам мальчиков
|
№ мальчика |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
1) Весёлый |
6 |
7 |
3 |
1 |
2 |
9 |
7 |
4 |
13 |
8 |
4 |
3 |
5 |
|
2) Спортивный |
3 |
3 |
0 |
1 |
1 |
22 |
0 |
15 |
1 |
4 |
0 |
12 |
10 |
|
3) Модный |
5 |
5 |
1 |
1 |
3 |
9 |
4 |
15 |
3 |
3 |
1 |
7 |
15 |
|
4)Дружелюбный |
7 |
10 |
3 |
2 |
9 |
1 |
6 |
3 |
7 |
9 |
5 |
6 |
4 |
|
5) Активный |
9 |
5 |
4 |
3 |
7 |
8 |
3 |
2 |
10 |
5 |
1 |
6 |
9 |
Приложение В
Нечёткие множества учеников нашего класса, построенные по методу привлечения равноправных экспертов
|
№ п/п |
Элемент нечёткого множества xi |
САМАЯ |
№ п/п |
Элемент нечёткого множества yi |
САМЫЙ |
||||||||
|
весёлая |
спортивная |
модная |
дружелюбная |
активная |
весёлый |
спортивный |
модный |
дружелюбный |
активный |
||||
|
1 |
x1 |
0,82 |
0,06 |
0,00 |
1,00 |
0,64 |
1 |
y1 |
0,46 |
0,14 |
0,33 |
0,70 |
0,90 |
|
2 |
x2 |
0,36 |
0,65 |
0,80 |
0,33 |
0,18 |
2 |
y2 |
0,54 |
0,14 |
0,33 |
1,00 |
0,50 |
|
3 |
x3 |
0,36 |
1,00 |
0,13 |
0,44 |
0,64 |
3 |
y3 |
0,23 |
0,00 |
0,07 |
0,30 |
0,40 |
|
4 |
x4 |
0,73 |
0,12 |
0,33 |
0,67 |
0,36 |
4 |
y4 |
0,08 |
0,05 |
0,07 |
0,20 |
0,30 |
|
5 |
x5 |
0,45 |
0,53 |
0,13 |
1,00 |
0,36 |
5 |
y5 |
0,15 |
0,05 |
0,20 |
0,90 |
0,70 |
|
6 |
x6 |
0,27 |
0,12 |
0,20 |
0,56 |
0,18 |
6 |
y6 |
0,69 |
1,00 |
0,60 |
0,10 |
0,80 |
|
7 |
x7 |
0,45 |
0,06 |
0,60 |
0,00 |
0,36 |
7 |
y7 |
0,54 |
0,00 |
0,27 |
0,60 |
0,30 |
|
8 |
x8 |
1,00 |
0,18 |
0,00 |
0,56 |
1,00 |
8 |
y8 |
0,31 |
0,68 |
1,00 |
0,30 |
0,20 |
|
9 |
x9 |
0,36 |
0,12 |
1,00 |
0,67 |
0,45 |
9 |
y9 |
1,00 |
0,05 |
0,20 |
0,70 |
1,00 |
|
10 |
x10 |
0,27 |
0,06 |
0,00 |
0,67 |
0,36 |
10 |
y10 |
0,62 |
0,18 |
0,20 |
0,90 |
0,50 |
|
11 |
x11 |
0,73 |
0,88 |
0,47 |
0,56 |
0,82 |
11 |
y11 |
0,31 |
0,00 |
0,07 |
0,50 |
0,10 |
|
12 |
x12 |
0,09 |
0,06 |
0,13 |
0,44 |
0,18 |
12 |
y12 |
0,23 |
0,55 |
0,47 |
0,60 |
0,60 |
|
13 |
x13 |
0,36 |
0,29 |
0,20 |
0,33 |
0,45 |
13 |
y13 |
0,38 |
0,45 |
1,00 |
0,40 |
0,90 |
|
14 |
x14 |
0,27 |
0,12 |
0,80 |
0,78 |
0,55 |
|||||||
Приложение Г
Нечёткие множества учеников нашего класса, построенные по методу привлечения равноправных экспертов
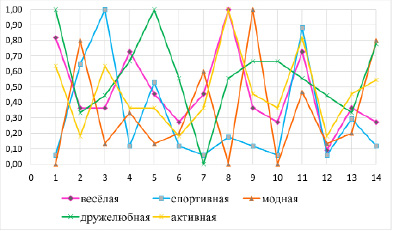
Рис. Г.1
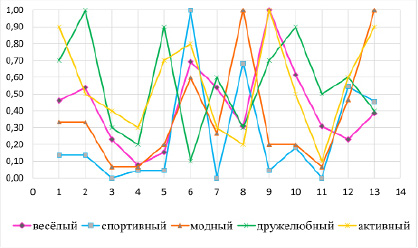
Рис. Г.2