• Авторы
• Научный руководитель
• Файлы
• Литература

Зименков И.А. 1

---

1 г. Мегион, ХМАО-Югра, МАОУ «СОШ №9», 11 класс

Никонов Ю.Д. (Мегион, МАОУ «СОШ №9»)

Статья в формате PDF

0 KB

1. Ежова К.В., Зверев В.А., Точилина Т.В. Линзовые концентрические системы // Научно-технический вестник информационных технологий, механики и оптики. – 2016. – Т. 16. № 2. – С. 224–236.

2. Заказное Н.П. и др. Теория оптических систем: Учебник для студентов приборостроительных специальностей вузов / Н.П. Заказнов, С.И. Кирюшин, В.Н. Кузичев. – 3-е изд., перераб. и доп. – М.: Машиностроение, 1992. – 448 с.

Актуальность. Гибкие стёкла получают всё больше и больше применений в современном мире, в том числе в мобильной и домашней электронике, оптических системах, архитектуре и др. В ходе анализа многих источников информации не удалось найти ни одного исследования на данную тему (на русском языке), однако, в нашей работе мы использовали некоторые наработки по изучению оптических свойств сферических концентрических линз, в том числе и статью К.В. Ежовой, В.А. Зверева и Т.В. Точилиной «Линзовые концентрические системы» [1].

С учётом развития нанотехнологий и необходимости применения в них оптических систем остро встаёт вопрос о необходимости изучения оптических свойств материалов, чтобы совершенствовать уже имеющиеся технологии, применяющие гибкое стекло, и создавать более эффективные конструкции с его использованием. Сложность изучения состоит в главном свойстве этого материала – гибкости, что следует из его названия, поэтому нужно провести ряд опытов и расчётов на тему исследования оптических свойств гибкого стекла.

Цель и задачи исследования: исследование оптических свойств гибкого стекла (на примере полимерной пленки) от его физических параметров (оптической плотности, радиуса изгиба, толщины).

Для достижения цели мы поставили перед собой следующие задачи:

• изучить уже имеющиеся статьи по этой теме;

• провести экспериментальное исследование физических параметров и оптических свойств стекла;

• построить математическую модель «приведённой» линзы;

• изучить на ее основе ход лучей через «приведённую» линзу и оптические свойства изогнутого стекла.

Гипотеза. Гибкое стекло в изогнутом состоянии обладает свойствами рассеивающей линзы, так как по краям изгиба стекла, «приведенная» толщина линзы будет больше, чем в центре.

Объектом исследования является гибкое стекло, предметом – оптические свойства гибкого стекла. Рассматриваются оптические свойства гибкого стекла малого радиуса изгиба. Ключевой идеей исследования линз с концентрическими сферическими поверхностями (совмещенные главные плоскости) является представление изогнутого стекла рассеивающей линзой с приведенной толщиной. Световые лучи, смещенные от оптической оси, на расстояниях сравнимых с радиусом кривизны стекла проходят больший путь – приведенную толщину.

Методика. В работе определен математический аппарат (онлайн модель), позволяющий определить ход лучей, преломляющие свойства линзы с различными подбираемыми конструктивными параметрами линзы с концентрическими сферическими поверхностями (радиус изгиба, толщина гибкого стекла). Введены коэффициенты, определяющие взаимосвязь внутреннего радиуса кривизны и толщины изогнутого стекла, что позволило преобразовать полученные аналитические соотношения в уравнение с двумя параметрами. Показано, что существование решения системы уравнений определяется оптическими константами выбранного материала стекла.

Гипотеза: гибкое стекло в изогнутом состоянии образует рассеивающую линзу, так как по краям изгиба толщина для однонаправленного пучка света, перпендикулярного стеклу в месте изгиба.

В процессе работы над проектом использовались следующие методы исследования: анализ, наблюдение, измерение, сравнение, обобщение.

Практическая часть

Определение угла Брюстера и коэффициента преломления гибкого стекла

Из-за невозможности получить доступ к образцам гибкого стекла (так как оно практически не выпускается серийно) было решено использовать тонкую ПВХ плёнку, у которой коэффициент преломления примерно равен среднему коэффициенту преломления у стёкол, которые чаще всего используются в вышеперечисленных сферах человеческой деятельности.

Опытным путём (табл. 1) было установлено, что используемые нами плёнки несколько толще, чем гибкое стекло, которое они заменяют (в 100 – 1000 раз).

Таблица 1

Измерение толщины плёнки способом рядов

Для измерения толщины был использован метод рядов, то есть измерение длины ряда одинаковых объектов с известным количеством объектов, из чего следует, что длинна одного объекта, если полученную длину ряда разделить на количество объектов.

Для определения угла Брюстера была собрана установка, включающая в себя стол с изменяемым углом наклона, на котором был закреплён образец плёнки, лимб для определения угла наклона стола, лазерная установка, штатив с закреплённым вращаемым поляроидом, экран и датчик освещённости (рис. 1).

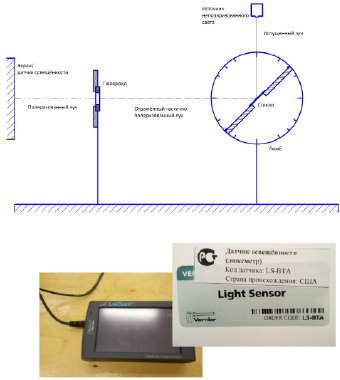
Рис. 1. Установка для определения угла Брюстера (вверху), люксметр (внизу)

Для определения угла Брюстера необходимо определить при каком угле падения луч света отражается полностью поляризованным. Для этого мы поместили образец на проворачивающийся стол и светили на него параллельно экрану, на который падает отражённый луч. Обязательным условием было то, чтобы отражённый частично или полностью поляризованный луч прошёл через поляроид, тогда можно было бы определить степень поляризации луча измерив интенсивность его свечения. Стол наклонялся на 5°, а при наклоне от 50° до 60° шаг уменьшился до 2°, чтобы повысить точность замеров в диапазоне, где, предположительно, должен был быть угол Брюстера для опытного образца. Полученные данные внесли в табл. 2.

Данные табл. 2 были представлены в виде графика (рис. 2) отчётливо видно, что при угле падения в 58°±1° свет почти не проходит через поляроид, что означает, что свет почти полностью поляризован, а отличное от нуля значение объясняется внешними световыми помехами (снятие показаний с датчика происходило в частично освещённой комнате).

Таблица 2

Зависимость поляризации света от его угла падения на материал

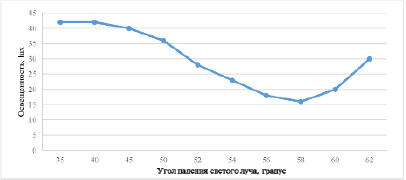
Рис. 2. График зависимости освещенности отраженного света от угла падения

tg(α)=n21 – формула угла Брюстера

n = tg (58°) ≈ 1,6003 – примерно равно n у гибкого стекла.

В подтверждение выдвинутой гипотезы был проведён ряд опытов, в ходе которых выявилась определённая корреляция между радиусом изгиба и степенью преломления света, то есть чем меньше радиус изгиба стекла, тем сильнее преломляется луч (Приложение 1).

Расчёт приведённой линзы

Вторым этапом нашей работы стало определение оптических свойств изогнутой плёнки, как тонкой линзы. Для этого необходимо определить толщину изогнутого стекла в каждой точке для параллельных главной оптической оси лучей света. Было получено математическое доказательство того, что при изгибании плёнки получается рассеивающая линза. Такому классу линз было дано название «приведённые», так как они дают представление об оптических свойствах изучаемого материала, но упрощают работу со сложной геометрией гибкого стекла. Оптические свойства такой линзы определяются исходя из радиуса изгиба стекла, его толщины и коэффициента преломления.

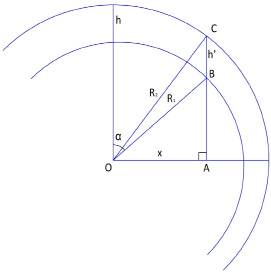
Рис. 3. Определение приведенной толщины изогнутой плёнки

h’ = h1

R2 = R1 + h

AO = OB cos (90 0 – α) = R1 sin (α)

R12 = AB2 + AO2 = AB2 + R1 sin (α)

R22 = AC2 + AO2 = AC2 + R1 sin (α)

;

;

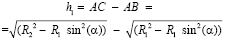
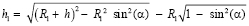
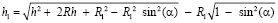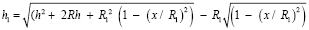R1 = r,

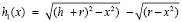– формула толщины приведённой линзы, где x – относительно главной оптической оси.

Именно так, согласно математической модели выглядит линза для пучка параллельных лучей.

У первой линзы (рис. 4, а) на большей её площади кривизна небольшая, а значит исследование стекла с радиусом изгиба более 1 мм (рис. 4, б) на искажение изображения нецелесообразно. Однако изучение свойств, как уже было сказано, производится не на стекле, а на полимерной плёнке, которая в 10–20 раз толще стекла (рис.5).

а б

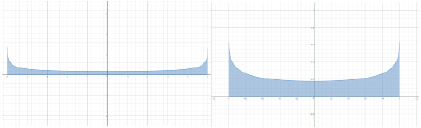
Рис. 4. Приведённая линза из плёнки с радиусом изгиба r = 5 мм (а), r = 1 мм (б)

а б

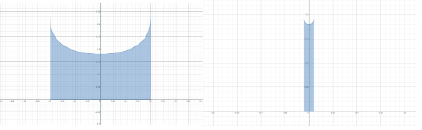
Рис. 5. Приведённая линза из плёнки с радиусом изгиба r = 0,2 мм (а), r = 0,01 мм (б)

Изучение хода лучей через приведённую линзу

Так как на нижней плоскости линзы параллельные лучи, которые перпендикулярны этой плоскости, не преломляются, то изучаться будет именно верхняя поверхность приведённой линзы.

Вычисляя производную, мы находим тангенс угла наклона линейной функции, являющейся касательной к графику в этой точке. Для того чтобы узнать под каким углом падают лучи на изогнутую поверхность линзы необходимо вычислить арктангенс для производной формулы h1(x) (Приложение 2).

Зависимость продольной сферической аберрации от радиуса изгиба

Одной из определяющих характеристик у линзы в качестве профессионального инструмента является продольная сферическая аберрация, точнее её минимизация. То есть для того, чтобы предлагать гибкое стекло в качестве материала для оптических систем следует изучить влияние его формы на продольную сферическую аберрацию.

Для изучения этой характеристики было составлено уравнение на основе ныне созданной математической компьютерной модели.

Но для начала необходимо было определить границы для подсчёта продольной сферической аберрации. Так как с изменением радиуса изгиба стекла меняется его кривизна, то и меняется расстояние от главного оптического до координаты, при которой начинается полное внутреннее отражение, а значит нельзя воспользоваться линейной функцией расчёта максимального отступа от оптического центра в зависимости от радиуса, но возможно составить квадратичную функцию, то есть вычислить изменение коэффициента у линейной функции при разных радиусах.

Все замеры производились на основе математической модели, данные таблицы отображены на графике (Приложение 3).

Прогрессия стремиться к линейной, а, значит, соответствует формуле:

y = (1.8–0.86)/(2–1)x – 0.08

k = 0.94r – 0.08

По этому коэффициенту будет рассчитываться координата крайней точки для вхождения луча в линзу относительно главного оптического центра без полного внутреннего отражения.

Для определения координаты ближайшего к главному оптическому центру луча будет использован следующий коэффициент: k = 0.0001. Так как это оптимальная точность для существующей математической модели.

Сводя всё вместе, мы можем описать универсальную формулу определения продольной сферической аберрации по двум точкам преломления луча, вычитая значения формулы (Приложение 2) для значений с вышеописанными коэффициентами.

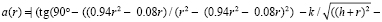
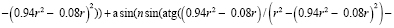
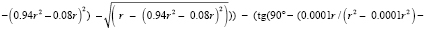
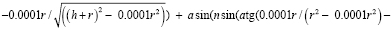
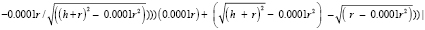
– общая формула просчёта продольной сферической аберрации по точкам преломления двух лучей.

Построим таблицу со значениями данной формулы для разных значений радиуса и построим соответствующий график (Приложение 4).

Заключение

Наша работа заключалась в исследование оптических свойств изогнутого гибкого стекла с применением как экспериментальных, так и теоретических способов.

Основные результаты. Представление изогнутого гибкого стекла (линзы с концентрическими поверхностями) как рассеивающую линзу с приведенной толщиной, позволило построить математическую модель расчета подобных оптических поверхностей.

Практическая значимость. Несомненная практическая значимость работы заключается в построении компьютерной математической модели изогнутого гибкого стекла (линзы с концентрическими поверхностями), содержащая основные параметры гибкого стекла позволяющая определить ход преломленных световых лучей и положение сферической аберрации.

Приложения

Исследование оптических свойств гибкого стекла

Приложение 1

Эксперименты с преломлением света в гибком стекле

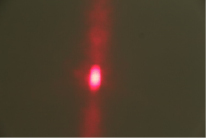
r = 1,48 мм r = 3,9 мм

Искажение красного луча лазера при освещении стекла с радиусом изгиба r

r = 1,48 мм r = 3,9 мм

Искажение зеленого луча лазера при освещении стекла с радиусом изгиба r

Приложение 2

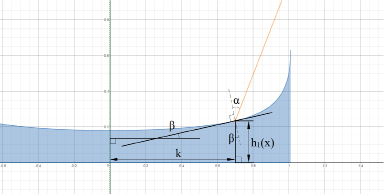
Изучение хода лучей через приведённую линзу

Угол падают лучи на изогнутую поверхность линзы вычисляем как арктангенс для производной формулы h1(x).

β(x) = arctg (h1(x)’),

где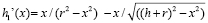

Из формулы

sin (α) / sin (β) = n.

Получаем

sin (α) = n sin (β).

Подставим в неё значение полученное ранее для того, чтобы узнать, как преломляется свет на границе сред

–

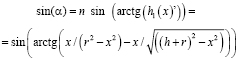
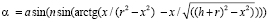формула угла преломления света на изогнутой поверхности линзы.

Для построения преломлённого луча используем формулу для построения прямой:

y = n/m x + b = tg α x + b.

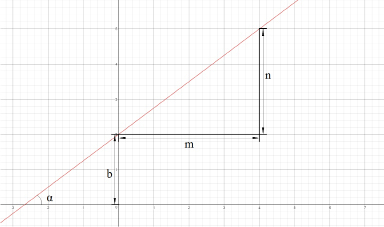
Немного видоизменив вышеописанную формулу для данной ситуации:

получаем:

–

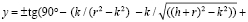
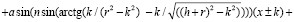
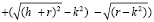общее уравнение преломления лучей в приведённой линзе для компьютерной модели, где k – отклонение от главной оптической оси –r ≤ k ≤ r

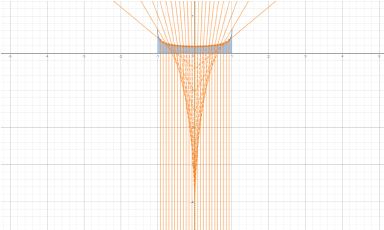
Ход лучей через линзу с радиусом изгиба r = 1 мм с k = 0,074 мм

Приложение 3

Максимальный отступ от главного оптического центра без полного внутреннего отражения (таблица, график)

Приложение 4

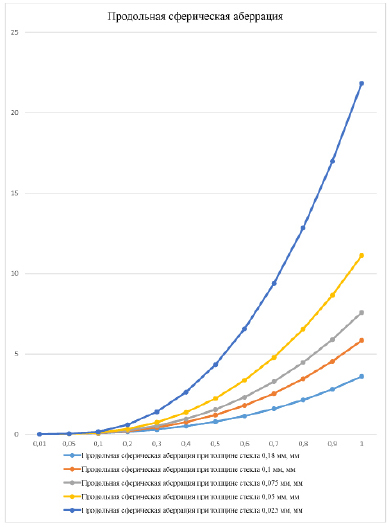
Значения продольной сферической аберрации для разных радиусов изгиба стекла, составленные на базе компьютерной модели

На основе таблицы можно заметить закономерность: a(r) ~ r / h.

Библиографическая ссылка