Цель исследования: узнать и рассказать о самых интересных и необычных парадоксах теории вероятностей.
“Существует три вида лжи: ложь, наглая ложь и статистика”
Марк Твен
Теория вероятностей – это раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Но ведь намного интереснее узнать её парадоксы, а не читать обычную теорию. Актуальность этой темы состоит в том, что, как и любая другая область науки, математика отражает противоречия окружающего нас мира. Поэтому история математики, естественно, полна интересных парадоксов, и некоторые из них послужили отправной точкой больших измерений. Особенно богата парадоксами математика случайного. По мнению Карла Пирсона (основателя математической статистики), в математике нет другого такого раздела, в котором столь же легко допустить ошибку, как в теории вероятностей.
Парадокс Монти Холла
Первый, и, пожалуй, самый интересный парадокс в теории вероятностей, решение которого, на первый взгляд, противоречит здравому смыслу.
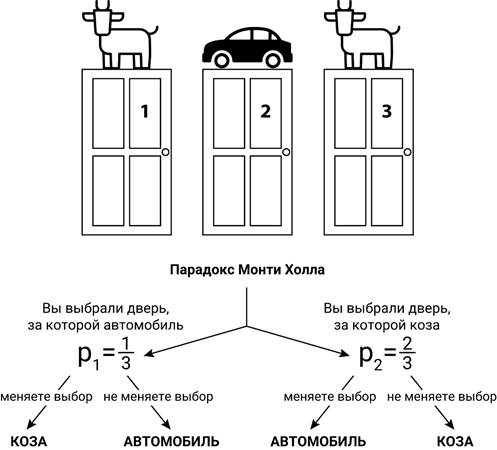
Парадокс назван так в честь ведущего американского телешоу – Монти Холла. Допустим вы попали на его телешоу и вам предложили сыграть с ним в игру. Вы вышли на сцену и перед вами выбор между тремя дверьми, за одной из которых машина, а за двумя другими находятся козы. Стоит учитывать, что ведущий заранее знает где расположена машина, а где козы. После того, как вы выбрали одну из трех дверей, ведущий открывает одну из оставшихся двух дверей, за которой расположена коза, после чего он предлагает вам изменить свое решение.
Многие подумают, что после того как ведущий открыл одну из дверей, ваши шансы составляют 50% на то, что за вашей дверью машина и 50% что за вашей дверью коза. Если вы тоже так подумали, то я вынужден вас огорчить, вы не правы! Давайте разберемся, почему это не так.
Предположим, что за первой дверью находится коза, за второй - машина и за третьей дверью – коза. И допустим в первом случае вы выбираете первую дверь, тогда ведущий вынужден открыть третью дверь. Если вы поменяете свое решение, то выиграете.
Во втором случае вы выбираете вторую дверь. Ведущий может открыть любую из двух оставшихся, но если вы поменяете свое решение, то проиграете.
В третьем случае вы выбираете третью дверь, тогда ведущий вынужден открыть первую дверь. Если вы поменяете свое решение, то выиграете.
Таким образом, если вы поменяете свое решение, то выиграете с шансом 66% , но это не отменяет того, что изначально вы могли выбрать дверь, за которой расположена машина.
Парадокс второго ребенка
Впервые этот парадокс придумал и сформулировал Мартин Гарднер и он звучит так: “ У мистера Смита двое детей. Хотя бы один ребенок – мальчик. Какова вероятность того, что и второй – тоже мальчик”?
Большая часть подумает, что правильный ответ – 50%. Вы правы, но только частично. Дело в том, что правильный ответ будет отличаться в зависимости от того, как мы подсчитываем вероятность того, что второй ребенок в семье мистера Смита – тоже мальчик.
Вариант 1
В первом случае, нам надо рассмотреть все комбинации в семьях, у которых двое детей, где Д - девочка, а М – мальчик: Д/Д; Д/М; М/Д; М/М.
Мы видим, что вариант Д/Д нам не подходит, так как по условию этой задачи, одним ребенком должен быть мальчик. Таким образом возможны три варианта, когда второй ребенок – мальчик. Следовательно, вероятность составляет 33%.
Вариант 2
Во втором случае нам надо представить, что вы встречаете мистера Смита в парке, когда он гуляет с детьми. Один из детей – мальчик. Какая вероятность того, что второй ребенок тоже мальчик? Так как пол второго ребенка не зависит от пола первого ребенка, то вероятность становится равной 50%.
Санкт-Петербургский парадокс
Впервые парадокс стал популярен благодаря Даниилу Бернулли, но иногда авторство этого парадокса приписывают Леонарду Эйлеру и связывают название с тем, что Эйлер продолжительное время жил в Петербурге.
Рассматривается следующая задача. Перед началом игры вы платите некоторую сумму, после чего подбрасываете монетку до тех пор, пока вам не выпадет орел. Когда выпадает орел, игра заканчивается и вы получаете выигранные вами деньги, которые рассчитываются по следующему правилу. Если вам выпал орел при первом же броске, вы получаете 20 рублей, если же орел выпал при втором броске, то вы получите 21 рублей и так далее.
Вопрос в этой задаче следующий: сколько надо внести денег вначале, чтобы игра стала справедливой?
Мы можем найти математическое ожидание вашего выигрыша, которое равно бесконечности:
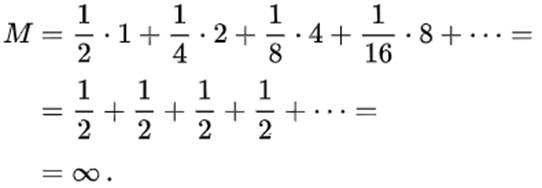
Парадокс состоит в том, что хоть и математическое ожидание вашего выигрыша равно бесконечности(больше любого возможного выигрыша), настоящие игроки чувствуют, что даже 20 рублей – очень высокая цена для начала этой игры.
По моему мнению, самый лучший ответ на эту задачу предложил Уильям Феллер. Если не использовать строго описание, то объяснение такое: играть в эту игру с большим количеством людей. После чего можно вычислить математическое ожидание выигрыша у каждого из игроков и, если оно будет расходиться, то требуется предположение о бесконечном времени для этой игры.
Заключение
Таким образом, было исследовано 3 парадокса теории вероятностей: парадокс Монти Холла, парадокс второго ребёнка и Санкт-петербургский парадокс. Также было составлено методическое пособие для расширения, углубления и лучшего усвоения знаний об этих парадоксах.
Библиографическая ссылка
Тулупов А.А. ПАРАДОКСЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ // Старт в науке. 2022. № 1. ;URL: https://science-start.ru/ru/article/view?id=2150 (дата обращения: 26.02.2026).
