Одной из самых удивительных современных гипотез является знаменитая гипотеза Коллатца которая утверждает, что в не зависимости от того с какого числа начинается процесс рано или поздно он заканчивается и приводит к единице. В настоящее время эта гипотеза проверена на вычислительных машинах для достаточно больших натуральных чисел. В прессе регулярно появляются сообщения о том, что кто-то доказал гипотезу, но официального подтверждения о доказательстве в общем случае не существует до сих пор.
Термин аттрактор достаточно современный, так как появился только в XX веке. Attract – в переводе с английского «притягивать», это такие состояния системы, в которые она стремится попасть из любого своего состояния. Существуют различные виды аттракторов: точечный аттрактор, предельный цикл, «странный аттрактор». Практическая ценность аттрактора в том, что с помощью них можно описывать поведение сложных систем [1].
Примером арифметического аттрактора является способ вычисления предложенный, например, Р. Бахтизиным [2]. Если взять любое двузначное число, состоящее из не одинаковых чисел, поменять цифры местами, затем найти разность этих чисел, и процесс повторить, то получим число 9. Последовательности как бы «притягиваются» к нему. Например, число 81, отнимем от него число 18 и продолжаем отнимать от результата, его «зеркальное» число: 81 – 18 = 63 – 36 = 27 – 72 = -45 – (- 54) = 9. С трехзначными числами получается число 99, а вот с четырехзначными числами аттракторов будет уже пять.
Еще один пример – числа Капрекара. Число 6174 имеет следующую особенность. Выберем любое четырёхзначное число n, больше 1000, в котором не все цифры одинаковы. Расположим цифры сначала в порядке возрастания, затем в порядке убывания. Вычтем из большего меньшее. Повторяя этот процесс с получающимися разностями, не более чем за семь шагов получим число 6174, которое будет затем воспроизводить само себя [3] .
Перейдем к гипотезе Коллатца. Гипотеза Коллатца касается алгоритма построения числовой последовательности, известного как HOTPO (Half Or Triple Plus One – половина или утроенное плюс один). В алгоритме на вход подается некоторое число xn (n-й член последовательности), а на выходе получается член последовательности с номером n + 1. При этом, если xn четное, то xn+1 равно половине xn . В противном случае xn+1 = 3xn + 1.
Легко видеть, что, если xn = 1, то на следующем шаге мы получим 4, а еще за два шага вернемся к единице, то есть, алгоритм зациклится [4].
Гипотеза. Вне зависимости от того, с какого числа мы начинаем, рано или поздно в нашей последовательности встретится единица и алгоритм сведется к простому циклу (зациклится). (1937 г., Лотар Коллатц).
Как заметил по этому поводу великий американский математик венгерского происхождения Пол Эрдёш, современная математика не имеет еще аппарата для доказательства гипотезы Коллатца и это показывает, что тема работы является актуальной.
За годы изучения задачи было установлено, что гипотеза Коллатца связана с решением разного рода задач из теории чисел, фрактальной геометрии и других областей математики.
В этой работе мы вводим целый класс арифметических аттракторов, определение которых основано на тех же принципах, что определение аттрактора Коллатца.
Определение. Пусть p ≥ 2- фиксированное натуральное число. Берем любое натуральное число. Если оно составное, то делим его на наименьший делитель, а если простое, то умножаем на p и прибавляем 1 (получаем px + 1). Над полученным числом выполняем те же самые действия, и так далее.
Число, получающееся в результате применения этих операций при данном p, будем называть p-аттрактором.
Например, пусть p = 2. Для числа x = 7 имеем: 7> 15> 5> 11> 23> 47> 95> 19> 39> 13> 27> 9> 3. Для числа x = 34 имеем: 34> 17> 35> 7> …> 3. Для числа x = 41 имеем: 41> 83> 167> 335> 67> 135> 27> 9 > 3. Итак, 2-аттрактор, видимо, равен 3. Эти вычисления позволяют нам сформулировать гипотезу, подтверждение которой требует дополнительных исследований.
Проведем расчеты с помощью электронных таблиц, построчного для каждого числа, вводя формулы и анализируя результаты. Так как по определению составное число делим на его наименьший делитель, пока не получим простое, то вычисления достаточно проводить только для простых чисел. Для начала исследования мы выбрали последовательность простых чисел, меньших 100. Результаты вычислений представим на рисунке 1. В таблице применено два правила для условного форматирования:
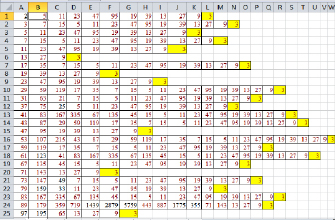
Рис. 1. Последовательность px + 1 для р = 2 и при простых x < 100
- заливка ячейки желтым цветом, когда значение равно 3;
- выделение красным цветом шрифта, если значения повторяющиеся.
Все вычисления цепочек значений для простых чисел, меньших 100 проведены полностью, для чисел до 503 полные цепочки не вычислялись, так как ясно, что достаточно получить число, встречающееся в ранее вычисленных последовательностях, что дает цепочку, проводящую к числу 3, как показано на рисунке 2. Желтым цветом выделены ячейки с простыми числами больше 503, для которых также уже ясен аттрактор. Таким образом, можем утверждать, что 2аттрактор равен, по-видимому, трем. Максимальное число, получившееся в наших вычислениях – 5759, максимальное число шагов в цепочке вычислений – 22. Для наглядного отображения значений вычислений построим цепочки вычислений при простых числах 2, 3, 5, 7 и 11, как показано на рисунке 3.
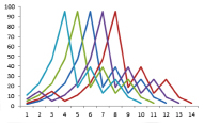
Рис. 3. График аттракторов при р = 2 и простых числах 2, 3, 5, 7 и 11
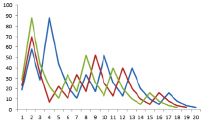
Рис. 4. Кривые аттрактора для р = 3 при простых числах 19, 23 и 29
Проведем вычисления при других значениях p. Пусть p =3, вычисления показывают, что 3аттрактор видимо равен 2. Рассмотрим график кривых для р = 3. Для наглядности оставим только три числа 19, 23, 29 (рисунок 4). Результаты вычислений показаны на рисунке 5. Желтым цветом выделены ячейки с простыми числами, большими по значению, чем исходное простое число последовательности, которое говорит о том, что для него предположение также верно. Самая длинная цепочка вычислений из числа 59 и равна 31-шагу. Максимальное значение в цепочке вычислений – 322.
Виду ограниченности объема статьи дальнейшие вычисления приведем без иллюстраций.
Пусть p = 4, вычисления показывают, что 4аттрактор видимо равен 5. Самая длинная цепочка вычислений из числа 83 и равна 27-шагам. Максимальное достигнутое значение в цепочке вычислений – 7013.
Пусть p = 5. Заметим, что 5аттрактор видимо равен двум. Самая длинная цепочка вычислений получилась для чисел 47 и 71 и равна 29-шагам. Максимальное число, полученное в цепочке вычислений – 1116.
Пусть p = 6. Проведем аналогичные вычисления. Для простых чисел меньших 47, 6аттрактор равен 13. Для простого числа 47 мы возвращаемся снова в 47. Возврат в 47 происходит и для простого числа 89. При вычислениях из простых чисел 47 и 89 в цепочках участвовал еще целый ряд простых чисел, таких как 107, 227, 283 и другие. Это говорит о том, что для них также аттрактором будет число 47. Можно утверждать, что при p = 6 мы имеем два аттрактора – 13 и 47. Самая длинная цепочка вычислений получилась для числа 13 и равна 36-шагам. Максимальное число, достигнутое в цепочках вычислений равно – 88099.
Пусть p = 7. Проведем аналогичные вычисления в электронной таблице. Получим, что аттрактором будет число 3. Самая длинная цепочка вычислений получилась для числа 53 и равна 35-шагам. Максимальное число, достигнутое в цепочках вычислений равно 1940.
Пусть p = 8. Получим, что аттрактором будет число 11. Самая длинная цепочка вычислений получилась для числа 71 и равна 45-шагам. Максимальное число, достигнутое в цепочках вычислений – 49065.
При р = 9 получаем два аттрактора – 13 и 37. Получаем 26 шагов в цепочке вычисления для числа 31 (аттрактор – 13) и 32 шага в цепочке вычисления для числа 9 (аттрактор – 37). Максимальное число, достигнутое в цепочках вычислений равно 3610.
При р = 10 на 58 шаге повторяется число 43 при вычислении от числа два. Можно предположить, что 10-аттрактор равен 43. Максимальное количество – 42 шага в цепочке вычисления для числа 41. Максимальное число, достигнутое в цепочках вычислений равно 159711.
Для р = 11 аттрактор по-видимому равен 17. Максимальное количество шагов в цепочке вычислений – 44, из числа 71. Максимальное число в вычислениях – 7052.
Подведем итоги вычислений в таблице. Для каждого р рассмотрим pаттрактор, максимальное количестве шагов в цепочке вычислений и полученное максимальное число. Результаты представлены в таблице.
Сводная таблица для р-аттракторов
|
№ п/п |
p |
p-аттрактор |
Максимальное количество шагов |
Максимальное число в цепочке |
|
2 |
3 |
22 |
5759 |
|
|
3 |
2 |
31 |
322 |
|
|
4 |
5 |
27 |
17013 |
|
|
5 |
2 |
29 |
1116 |
|
|
6 |
13, 47 |
36 и 20 |
88099 |
|
|
7 |
3 |
35 |
1940 |
|
|
8 |
11 |
44 |
49065 |
|
|
9 |
13, 37 |
26 и 32 |
3610 |
|
|
10 |
43 |
42 |
159711 |
|
|
11 |
17 |
44 |
7052 |
Нерешенные задачи и гипотеза
Гипотеза. Предполагаем, что для простых значений р числовая последовательность px + 1 имеет точно один аттрактор, для составных значений р это необязательно.
Продолжим вычисления для простого р = 13. Вычислим последовательности для простых значений x < 100 при p = 13. Результаты вычислений представлены на рисунке 6. Как видно из рисунка мы имеем два аттрактора – 3 и 19. Самую длинную цепочку вычислений получаем из числа 67 и она составляет 76 шагов. Максимальное число – 20372.
Как видим вычисления для р = 13 показывают, что наша гипотеза неверна и требуются дальнейшие исследования.
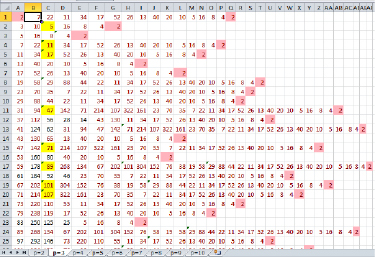
Рис. 5. Последовательность px + 1 для р = 3 при простых x < 100

Рис. 6. Последовательность px + 1 для р = 13 при простых x < 100
Заключение
В данном исследовании мы рассмотрели новый вид последовательности, вычисление членов которого приводит к зацикливанию.
Математическая новизна результатов работы заключается в самой новой конструкции серии арифметических аттракторов. Несмотря на отсутствие теорем в этом исследовании, эта конструкция представляет интерес, т.к. кажется на первый взгляд более простой, чем гипотеза Коллатца.
Мы выдвинули гипотезу, что единственный аттрактор возможен при простом значении р. Когда мы продолжили вычисления при р = 13 оказалось, что при этом р имеются два аттрактора – 3 и 19. А именно, при вычислении из простых чисел х = 2, 3, 5, …, 17 мы приходим к 3, а при х = 19, 31, 73, 101 мы получаем 19. Не ясно для вычисленных значений р также ведут себя последовательности или при больших значениях х появляются еще аттракторы. Также пока не ясно существует ли еще простое р при котором получаем несколько аттракторов. Также не ясно существуют ли р, при которых получается больше двух аттракторов.
Нерешенные задачи:
- Доказать, что для любого p, аттрактор возможно состоящий из нескольких точек, существует.
- Найти все значения p, при которых аттрактор состоит из одной точки.
Эти задачи пока не решены. В своё оправдание могу отметить, что гипотеза Коллатца несмотря на усилия мировых математиков до сих пор не доказана. Для разрешения поставленных вопросов необходимо продолжить наши вычисления для других р. Необходимо написать программу для вычислений на компьютере, так как дальнейшие вычисления достаточно трудоёмкие. Доказательство выдвинутых гипотез является направлением дальнейших исследований.
Библиографическая ссылка
Камальдинов И.Р. АРИФМЕТИЧЕСКИЕ АТТРАКТОРЫ ВИДА PX + 1 // Старт в науке. 2017. № 5-1. ;URL: https://science-start.ru/ru/article/view?id=762 (дата обращения: 11.07.2025).
