В данной работе систематически используется операция логарифмирования, тесно связанная с операцией возведения в степень. Напомним, что логарифм числа х по основанию a есть показатель той степени, в какую нужно возвести а, чтобы получить х. Ниже представлены некоторые свойства степеней и логарифмов:
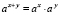
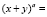Бином Ньютона
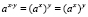
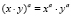
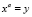
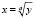
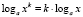
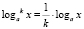
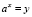
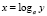
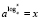
Отправной точкой для данного исследования послужило свойство:
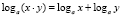
Оно вызвало у меня 2 вопроса:
– логарифм суммы равен какой операции над логарифмами слагаемых?
– логарифм какой операции равен произведению логарифмов операндов?
(операнд – аргумент операции), то есть
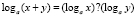
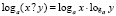
Среди общеизвестных свойств логарифмов эти свойства отсутствуют.
Это не случайно. В книге [1] на стр. 160 читаем:
«Отметим еще малоизвестную коммутативную и ассоциативную операцию, ступенью ниже сложения, относительно которой сложение, как легко убедиться, дистрибутивно:
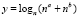
Определенная так функция двух переменных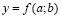 
и есть, очевидно, та функция от log x и log y, которая выражает log(x + y) через log x и log y: log(x + y) = f(log x, log y).»
К сожалению, автор [1] не указывает тот источник из (довольно представительного на то время – 1938 год) списка литературы, в котором впервые была указана эта малоизвестная операция. Сам автор пишет:
«Имея в виду сравнительную элементарность вопросов, я позволил себе не наводить литературных справок и потому лишен возможности сослаться на какие-либо литературные источники по указанным (этому и другим) пунктам.»
Следует отметить, что упоминание об указанной малоизвестной операции, ступенью ниже сложения, завершает «§ 45. Операции высших ступеней» «Главы V. Операторная теория действий третьей ступени»; понимая под операцией первой ступени сложение, а второй – умножение, автор подробно рассматривает в указанной главе операцию третьей ступени, а в указанном параграфе намечает «само собой напрашивающийся вопрос об операциях четвертой и высших ступеней».
Современное изложение этих вопросов, без ссылки на книгу [1], содержится в работе [2], посвященной «естественной цепи бинарных арифметических операций». Операции определяются с использованием обозначаемых через ln натуральных логарифмов, для которых фигурирующее выше η равно числу е – основанию натуральных логарифмов, причем ex часто обозначается exp x. В силу этого определения ln ex = x, exp ln x = x.
Именно в рамках этой цепи справедливо общее свойство логарифмов
.
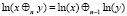При этом цепь определяется следующими соотношениями:
– для n = 0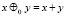 
,
так что, в отличие от [1], обычное сложение является операцией не первой, а нулевой ступени;
– для n ≤ 0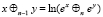 
;
– для n ≥ 0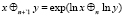 
.
В силу последнего определения при n = 0
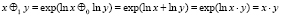
оказывается обычным умножением – операцией не второй, а первой ступени в отличие от [1]; рассмотренная в [1] операция третьей ступени оказывается операцией второй ступени
.
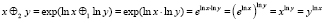Теперь:
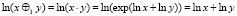– общеизвестное свойство;
,
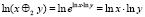что дает ответ на второй вопрос;
если же положить в первом определении n = 0,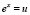 
, 
, 
, 
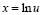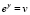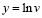, то
,
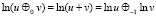что дает ответ на первый вопрос – ответ, совпадающий с указанным в [1].
Поскольку мы столкнулись с «нестандартными» числовыми операциями, мне стало интересно, образуют ли пары этих операций числовые поля. Для того, чтобы узнать это, проверим пары операций на аксиомах поля действительных чисел.
Далее используем тройную нумерацию: первое число – индекс первой операции пары, второе – номер операции пары (первая или вторая; в последней аксиоме, связывающей операции, на этом месте стоит 3), третье – номер аксиомы. Кроме того, далее будем обозначать операцию ⊕–1 знаком ⊕, без какого-либо индекса.
Вот всем известная пара операций, обычное сложение и обычное умножение <⊕0; ⊕1>, удовлетворяющая аксиомам числового поля – именно для них были впервые сформулированы эти аксиомы:
0.1.1.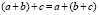 
(ассоциативность) +
0.1.2.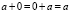 
(существование нейтрального элемента) +
0.1.3.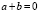 
(существование противоположного элемента: b = -a) +
0.1.4.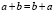 
(коммутативность) +
0.2.1.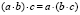 
(ассоциативность) +
0.2.2.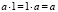 
(существование нейтрального элемента) +
0.2.3.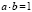 
(существование обратного элемента: b = 1/a) +
0.2.4.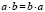 
(коммутативность) +
0.3.1.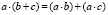 
(дистрибутивность) +
Теперь делаем то же с парой <⊕–1; ⊕0>, когда сложение необычное, а роль умножения играет обычное сложение:
-1.1.1. (a⊕b)⊕c = a(b⊕c) (ассоциативность) +
-1.1.2. -∞⊕a = a⊕-∞ = a (существование нейтрального элемента) +
-1.1.3. a⊕b = -∞ (существование противоположного элемента) -
-1.1.4. a⊕b = b⊕a (коммутативность) +
-1.2.1. (a + b) + c = a + (b + c) (ассоциативность) +
-1.2.2.(a + 0) = (0 + a) = a (существование нейтрального элемента) +
-1.2.3. a + b = 0 (существование обратного элемента: b = -a) +
-1.2.4. a + b = b + a (коммутативность) +
-1.3.1. a⊕b + c = (a + с)⊕(b + c) (дистрибутивность) +
Здесь мы видим, что аксиома -1.1.3. не выполняется, отсюда делаем вывод, что множество чисел с этими операциями поля не образует – отсутствует противоположный элемент; в этом случае говорят о полуполе.
Третья пара операций <⊕1; ⊕2>, роль сложения играет обычное умножение, а умножение необычное:
1.1.1.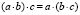 
(ассоциативность) +
1.1.2.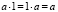 
(существование нейтрального элемента) +
1.1.3.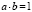 
(существование противоположного элемента: b = 1/a) +
1.1.4.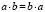 
(коммутативность) +
1.2.1.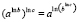 
(ассоциативность) +
1.2.2.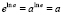 
(существование нейтрального элемента) +
1.2.3.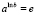 
(существование обратного элемента, 
) +
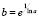1.2.4.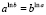 
(коммутативность) +
1.3.1.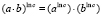 
(дистрибутивность) +
Делаем вывод: множество чисел с этой парой операций образует поле.
Проверим справедливость некоторых аксиом:
1.2.1: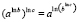
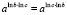
1.2.2: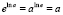 
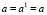
1.2.3: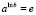 
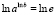
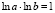
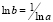
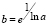
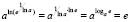
1.2.4: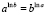 
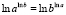
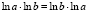
Выводы
В ходе работы мы нашли как операцию, выражающую логарифм суммы через логарифмы слагаемых, так и операцию, логарифм которой равен произведению логарифмов операндов. Так же мы узнали, образует ли множество чисел с «нестандартными» парами операций числовые поля. При этом возникла отличная от числового поля структура – полуполе.
Направление дальнейших исследований – проверить аксиомы для других пар операций цепи из [2] и определить возникающие при этом алгебраические структуры.
Библиографическая ссылка
Насонов И.В. НЕСТАНДАРТНЫЕ СВОЙСТВА ЛОГАРИФМОВ И ЦЕПЬ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ // Старт в науке. – 2017. – № 4-1. ;URL: https://science-start.ru/ru/article/view?id=677 (дата обращения: 21.11.2024).