Текстовые задачи – одни из самых сложных задач в школьном курсе математики. Алгебраический метод решения не всегда бывает удобным для решения задач подобного типа – нередко бывает сложным выбрать нужную неизвестную величину так, чтобы решение было максимально простым и понятным.
С каждым годом текстовые задачи в школьном курсе математики усложняются, причем времени на совершенствование решений этих задач практически не выделяется. И если раньше их решение не вызывало особых затруднений, то теперь с этим могут возникнуть некоторые трудности. Поэтому решить задачу стандартным способом вряд ли получится. Решая одну из текстовых задач, я решила обратиться к математическому моделированию.
Для того чтобы устранить эти трудности, я решила рассмотреть другие возможные методы решения этих задач, а в частности задач на движение по окружности. Предметом моего исследования является математическое моделирование, как процесс, без которого, на мой взгляд, решение подобных задач будет наиболее трудоемким или даже невозможным.
Цель работы – рассмотреть основные виды математических моделей, применяемых к решению математических задач, и выбрать наиболее оптимальные к конкретной из них. К постановке этой цели меня привела следующая проблема: в современном мире, насыщенном информацией, необходимо умение представлять информацию в доступном (упрощенном) виде с целью достижения результата (решения задачи).
Исходя из цели, были поставлены следующие задачи:
- Проанализировать научно – учебную литературу по теме работы.
- Рассмотреть процесс математического моделирования и этапы создания модели для конкретной задачи.
- Рассмотреть этапы создания математической модели.
- Научиться составлять математические модели различного типа.
- Выявить оптимальный метод математического моделирования для решения конкретной задачи (подобрать оптимальные модели для решения определённого типа задач).
Гипотеза: Существует универсальная математическая модель, с помощью которой можно решить любую текстовую задачу.
Объект исследования: текстовые задачи различного типа.
Методы исследования: анализ, аналогия, обобщение, прогнозирование, эксперимент.
Основная часть.
Глава I. Что такое математическая модель?
1.1 Краткая теоретическая справка.
Заинтересовавшись математическим моделированием, я проанализировала литературу, подробно описывающую данный метод. Существуют различные трактовки и классификации этого понятия. Я остановилась на учебном пособии [1] И.А. Печерских и А.Г. Семенова, которые дают следующее определение математической модели:
Математическая модель представляет собой формализованное описание системы на некотором абстрактном языке, например, в виде совокупности математических соотношений, т. е. такое математическое описание, которое обеспечивает имитацию работы систем или устройств на уровне, достаточно близком к их реальному поведению. Любая математическая модель описывает реальный объект, явление или процесс с некоторой степенью приближения к действительности. Целью математического моделирования является анализ реальных процессов математическими методами.
1.2 Этапы математического моделирования.
1. Постановка задачи.
На этом этапе требуется четкое понимание поставленной задачи.
2. Изучение теоретических основ и сбор информации об объекте оригинала.
На этом этапе подбирается или разрабатывается подходящая теория
3. Формализация.
Заключается в выборе системы условных обозначений.
4. Выбор метода решения.
На этом этапе устанавливаются окончательные параметры моделей с учетом условия функционирования объекта.
5. Реализация модели.
Выполнятся построение математической модели (строится график, таблица, Рисунок или эскиз, граф) и решается задача исходя из новых условий.
6. Анализ полученной информации.
Сопоставляется полученное и предполагаемое решение.
7. Проверка адекватности реальному объекту.
Результаты, полученные по модели, сопоставляются с условиями исходной задачи.
Глава II. Применение моделирования к решению задачи.
Для достижения поставленной цели я составила несколько математических моделей, и постаралась к решению одной задачи (на движение по окружности) применить этот метод.
Задача.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 18 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 25 км/ч больше скорости другого?
Данную задачу решим с помощью математических моделей:
1. Таблица.
2. «Математический маятник».
3. Графическая модель.
2.1 Таблица – математическая модель, которая помогает упорядочить все данные в задаче для более удобного восприятия.
(Приложение 1. Таблица. Стр. 14.)
Решение.
Пусть x км\ч – скорость первого мотоциклиста, тогда скорость 2 – го мотоциклиста ( x + 25) км/ч. Пусть первый раз мотоциклисты поравняются через t часов. Для того, чтобы мотоциклисты поравнялись, более быстрый (то есть второй ) должен преодолеть изначально разделяющее их расстояние, равное половине длины всей трассы ( т.к. мотоциклисты расположены в диаметрально противоположных точках ) →
( x + 25 )t – xt = 9
tx + 25t – tx = 9
25t = 9
t = 21,6 (минут)
Ответ: 21,6 минут.
2.2 «Математический маятник».
Математическим маятником [2] называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Математический маятник имеет следующие характеРистики: период, частота колебаний, количество колебаний и длина нити, но для решения этой задачи я остановилась на двух из них: период частота. Если связать эти величины со скоростью, временем и расстоянием, то задачу на движение по окружности можно будет решать с помощью формул, которые свойственны математическому маятнику.
T – период – это время, затраченное на один круг. 
υ – частота колебаний – это величина обратная периоду.
Составим математическую модель.
(Приложение 2. «Математический маятник». Стр.14).
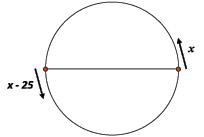
Пусть х км/ч – скорость первого мотоциклиста, тогда скорость второго мотоциклиста (х+25) км/ч. Длина всей трассы 18 км.
Т1 = 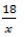
– время, затраченное 1 – ым мотоциклистом на прохождение полного круга (период).
Т2 = 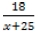
– время, затраченное 2 – ым мотоциклистом на прохождение полного круга (период).
Для того чтобы мотоциклисты поравнялись в первый раз их частоты должны совпасть, значит:
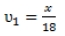
– частота первого мотоциклиста.
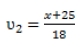
– частота второго мотоциклиста.
Тогда разность
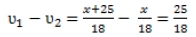
– частота с которой будут происходить встречи при старте из одной точки.
Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:
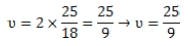
Тогда 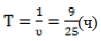 = 21,6 (мин.)
= 21,6 (мин.)
Ответ: 21,6 мин.
2.3 Графическая модель.
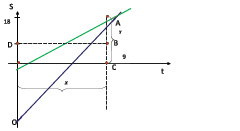
Графики законов, которые описывают зависимость S от t, строятся в системе координат SOt. Поскольку t > 0 и S > О, то построения выполняются в первой координатной четверти.
График движения тела по окружности можно заменить графиком движения по прямой. Обход телом окружности и возвращение в исходную точку равносильны достижению телом на прямой точки, удаленной от начальной на расстояние S0, равное длине окружности.
Изобразим схематически в системе SOt движение мотоциклистов.
Так как все величины положительны, то достаточно рассмотреть графики в первой четверти.
Пусть x ч – время, за которое первый мотоциклист догнал второго, y км – путь, пройденный вторым мотоциклистом до момента встречи с первым. Решение сводится к решению геометрической задачи.
(Приложение 3. Графическая модель. Стр. 15)
ΔACO - прямоугольный;
т.к. АС - перпендикуляр к оси Ox.
ΔADB - прямоугольный,
т.к. B перпендикуляр к DB.
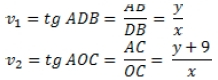
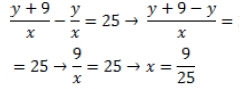
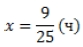 = 21,6 (мин)
= 21,6 (мин)
Ответ: 21, 6 минуты.
На примере решения данной задачи были выявлены следующие преимущества решения задач с помощью геометрической модели: наглядность, оперативность, простота решения.
Глава 3. Выявление оптимальных моделей для решения конкретных задач.
3.1 Задачи на совместную работу.
Задачи подобного типа удобнее всего решать с помощью таблицы, потому что производительность, объем работы и время на выполнение всей работы можно легко связать со скоростью, временем и расстоянием. Роль скорости выполняет производительность труда, роль расстояния – вся работа, время выполняет свою роль.
Задача.
Двое рабочих, работая вместе, могут выполнить производственное задание за 40 дней. За сколько дней может выполнить задание каждый из них, работая самостоятельно, если одному из них для этого надо на 18 дней больше, чем другому?
Решение:
Примем весь объем работы за единицу. Пусть 2 – ой рабочий, работая самостоятельно, может выполнить все задание за x дней, тогда 1 – ый — за (x+18) дней.
(Приложение 4. Таблица. Стр. 15)
Вместе за 1 день рабочие выполняют
задания. За 40 дней рабочие выполнят всю работу. Составим уравнение:
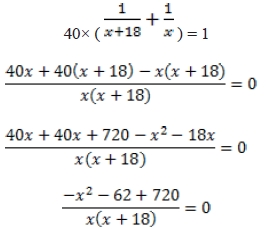
x(x+18) ≠ 0 → x ≠ 0, x ≠ -18 -x2 - 62 + 720 = 0 → x1 = 10, x2 = - 72 - не имеет смысла.
Второй корень не подходит по смыслу задачи (так как время не может быть отрицательным числом). Значит, 2 – ой рабочий, работая самостоятельно, может выполнить всю работу за 10 дней, а 1 – ый — за 10+9=19 дней.
Ответ: 10 дней, 19 дней.
3.2 Задачи на движение.
Задачи на движение по прямой удобнее всего решать с помощью графической модели.
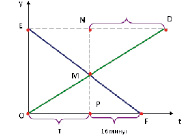
Задача: Два пешехода вышли одновременно из своих сел W и C навстречу друг другу. После встречи первый шел 25 минут до села C, а второй шел 16 минут до села W. Сколько минут они шли до встречи?
(Приложение 5. Графическая модель. Стр. 16)
Решение:
Пусть ОЕ расстояние между сёлами W и C. OD – график движения первого пешехода ( который шёл медленнее), а EF – график движения второго. М – место встречи.
1) ΔMND∼ΔMPO, 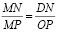
2) ΔMNE∼ΔMPF, 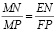
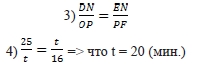
Ответ: 20 мин.
3.3 Задачи на движение по окружности.
Два велосипедиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение:
Используя модель «математического маятника», описанного выше, задача решается практически устно. 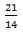
Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:
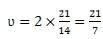 Тогда
Тогда 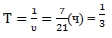 (ч) =
(ч) =
(ч) = 20 (мин.)
Ответ: через 20 минут.
С помощью этой модели можно также быстро решать задачи, в которых отставание составляет не половину трассы, а конкретное расстояние. Решим эту же задачу, изменив в ней условие.
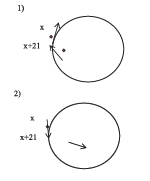
Два велосипедиста стартуют одновременно в одном направлении из двух точек круговой трассы, расстояние между которыми равно 3 км. Длина трассы равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение: Задача будет иметь 2 решения в зависимости от направления
движения по круговой трассе.
Составим математическую модель (для данной задачи их будет две).
(Приложение 6. «Математический маятник». Стр. 16)
В первом случае решение будет таким:
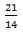 – частота, с которой будут происходить встречи при старте из одной точки.
– частота, с которой будут происходить встречи при старте из одной точки.
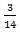 – часть периода (отставание), тогда
– часть периода (отставание), тогда
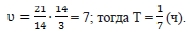
Во втором случае
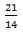 – частота, с которой будут происходить встречи при старте из одной точки.
– частота, с которой будут происходить встречи при старте из одной точки.
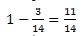
– часть периода (отставание), тогда
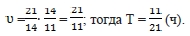
Ответ: через 1/7часа; или через 11/21 часа.
Таким образом, модель «Математический маятник» подходит для решения задач на движение по окружности. Применение такого способа решения значительно сокращает время на решение задачи, что позволит при выполнении контрольных работ и на экзамене увеличить время на решение более трудных задач.
Заключение.
В результате исследования были получены следующие результаты:
Был изучен процесс математического моделирования и этапы создания модели для конкретной задачи.
В ходе исследования была опровергнута гипотеза, о существовании универсальной математической модели для решения всех типов задач.
Я научилась составлять математические модели различного типа.
Были выявлены оптимальные математические модели для решения конкретной задачи.
Я думаю, что за моделированием – будущее. Умение составлять математические модели сможет помочь в решении задач из различных отраслей науки, а также жизненных задач. Хочется отметить, что решение задач с применением моделирования активизирует мыслительную деятельность, помогает лучше понять задачу, самостоятельно найти рациональный путь ее решения, установить подходящий способ проверки, определить условия, при которых задача имеет (или не имеет) решения. Работа с моделью позволяет яснее увидеть зависимости между данными и искомыми величинами, оценить задачу в целом, продемонстрировать разные варианты решения.
Приложения
Приложение 1. Таблица
|
V (км/ч) |
t (ч) |
S (км) |
|
|
1 – ый мотоциклист |
X |
t |
xt |
|
2 – ой мотоциклист |
(х+25) |
t |
( x + 25 )t |
Приложение 2. «Математический маятник»
Приложение 3. Графическая модель
Приложение 4. Таблица
|
Производительность труда |
Время работы |
Работа |
|
|
1 – ый рабочий |
1/(x+18)ч/день |
(x+18) дней |
1часть |
|
2 – ой рабочий |
1/x ч/день |
x дней |
1часть |
Приложение 5. Графическая модель
Приложение 6. «Математический маятник»
Библиографическая ссылка
Суслова Д.А. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ТЕКСТОВЫХ ЗАДАЧАХ // Старт в науке. 2017. № 2. ;URL: https://science-start.ru/ru/article/view?id=578 (дата обращения: 17.07.2025).
