В настоящее время актуальным вопросом становится проблема соотношения, изучаемого в школьном курсе математики, материла с жизнью. В 9 классе мы изучаем прогрессии: даем определение, учимся находить по формуламлюбой член прогрессии, сумму первых членов прогрессии. В заданиях ОГЭ используются задачи на применение основных формул прогрессий, но как эти понятия связаны с жизнью. В заданиях ЕГЭ по математике также есть задачи на применение арифметической и геометрической прогрессий, но уже с практическим содержанием.
В данной работе мы хотим найти ответы на вопросы: имеет ли это какое – либо практическое значение и как давно люди знают последовательности, как возникло это понятие, мы подтвердим или опровергнем утверждение о том, что математика – наука очень древняя и возникла она из практических нужд человека, что алгебра является частью общечеловеческой культуры.
Проблемный вопрос:
Действительно ли прогрессии играютбольшую роль в повседневной жизни?
- Объект исследования: последовательности: арифметическая и геометрическая прогрессии.
- Предмет исследования: практическое применение этих прогрессий
Гипотеза исследования:
На уроках математики мы много раз слышали о том, что математика – наука очень древняя и возникла она из практических нужд человека. Видимо, и прогрессии имеют определенное практическое значение.
Цель исследования: установить картину возникновенияпонятия прогрессии и выявить примерыих применения, создать сборник задач с практическим применением прогрессий с решением, так как в задачах ЕГЭ можно встретить задачи на прогрессии.
Практическое применение арифметической и геометрической прогрессий
Историческая справка
Первые представления об арифметической и геометрической прогрессиях были еще у древних народов. О прогрессиях и их суммах знали древнегреческие ученые. Архимед (III в. до н.э.) для нахождения площадей и объемов фигур вывел формулу суммы квадратов натуральных чисел.
12 + 22 + 32 + ……… + n2 = = 1/6 n(n + 1)(2n + 1).
Термин «прогрессия» (от латинского progression, что означает «движение вперед») был введен римским автором Боэцием (VI в.).
Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (III в.).
Известна интересная история о знаменитом немецком математике К. Гауссе (1777-1855), которыйеще в детстве обнаружил выдающиеся способности к математике. Учитель предложил ему сложить натуральные числа от 1 до 100. Маленький гаусс решил эту задачу за 1 минуту.
В истории математики: Величайший немецкий математик, астроном и физик Карл Гаусс родился в городе Брауншвейг (Германия). Его отец, садовник и фонтанный мастер, славился искусством быстро и легко считать. Эта способность перешла к сыну, говорившему позднее, что он «умел считать раньше, чем говорить». Первый успех пришёл к Гауссу в 9 лет. Школьный учитель велел ученикам найти сумму целых чисел от 1 до 40. Он рассчитывал надолго занять учеников этой задачей. Но Гаусс мгновенно сообразил, как сгруппировать слагаемые, и выдал ответ:
(1 + 40) + (2 + 39) + (3 + 38) + …. = = 40–21 = 820.
Найдите формулу, с помощью которой можно быстро вычислить сумму целых чисел от 1 до n.
Решение. Из формулы
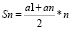
сразу получаем, что искомая сумма равна
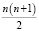
Сведения, связанные с прогрессиями, впервые встречаются в дошедших до насдокументах Древней Греции. Уже в V в. до н.э. греки знали следующие прогрессии и их суммы:
1 + 2 + 3 + ….. + n =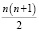 
2 + 4 + 6 + ….. + n = n(n + 1)
Древний Египет. Формула, которой пользовались египтяне: Задача из египетского папируса Ахмеса: «Пусть тебе сказано: раздели 10 мер ячменя между 10 человеками, разность же между каждым человеком и его соседом равна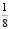 
меры».
Формула, которой пользовались египтяне:
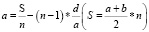
Задача из папируса Райнда «У семи лиц по семи кошек; каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?» Решение задачи Людей всего 7, кошек 72 = 49, они съедают всего 73 = 343 мыши, которые съедают всего 74 = 2401 колосьев, из них вырастает 75 = 16807 мер ячменя, в сумме эти числа дают 19 607.
Определения и формулы
Определение арифметической прогрессии:
Последовательность (an), каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией. Число d – разность прогрессии. Таким образом, арифметическая прогрессия есть последовательность, заданная рекуррентно равенством an + 1= an + d
Разность арифметической прогрессии:
d = an + 1 – an
1. Если d > 0, то (an) – возрастающая
2. Если d < 0, то (an) – убывающая
3. Если d = 0, то (an) – постоянна
Последовательность (an) является арифметической прогрессией тогда и только тогда, когда любой ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов, то есть d < 0.
Сумма членов арифметической прогрессии, равноудаленных от концов прогрессии, есть величина постоянная, то есть
a1 + an = a2 + an-1 = ….
Формула n-го члена арифметической прогрессии:
an = a1 + d(n –1)
Формулы суммы n первых членов арифметической прогрессии:
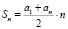
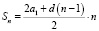
Определение геометрической прогрессии:
Последовательность (bn), первый член которой отличен от нуля и каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же отличное от нуля число q, называется геометрической прогрессией. Число q – знаменатель прогрессии. Таким образом, геометрическая прогрессия есть последовательность, заданная рекуррентно равенством
bn + 1 = bnq,
где b1 0, q 0.
Отношение любого члена геометрической прогрессии и ему предшествующего члена, равно одному и тому же числу q:
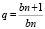
1. Если q > 0, (q 1), то (bn) – монотонна
2. Если q = 1, то (bn) – постоянна
Последовательность (bn) является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, есть среднее геометрическое соседних с ним членов, то есть
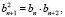
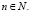
Произведение членов геометрической прогрессии, равностоящих от концов прогрессии, есть величина постоянная.
Формула n-ого члена геометрической прогрессии:
bn = b1·qn –1,
где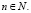 
Формулы суммы n членов геометрической прогрессии:
1. 
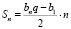, q 1
2. 
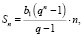q 1
3. Сумма бесконечной геометрической прогрессии при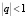 
равна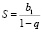 
.
Применение прогрессий в разных отраслях
Химия. При повышении температуры по арифметической прогрессии скорость химических реакций растет по геометрической прогрессии.
Геометрия. Вписанные друг в друга правильные треугольники образуютгеометрическую прогрессию.
Физика. И в физических процессах встречается эта закономерность. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их еще на 4 части и т.д. – это геометрическая прогрессия.
Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, через одинаковый промежуток времени их число удваивается.
В литературе: «…Не мог он ямба от хорея Как мы не бились отличить…». Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха.
Ямб – это стихотворный размер с ударением на четных слогах 2; 4; 6; 8;…Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2.
Хорей – это стихотворный размер с ударением на нечетные слогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7;..
Примеры.
Ямб. «Мой дЯдясАмыхчЕстныхпрАвил…», прогрессия 2; 4; 6; 8;…
Так бей, не знай отдохновенья,
Пусть жила жизни глубока:
Алмаз горит издалека –
Дроби, мой гневный ямб, каменья!
(А. Блок)
Хорей. «Я пропАл, как звЕрь в загОне» Б.Л. Пастернак, «БУря мглОю нЕбо крОет» А.С. Пушкин, прогрессия 1; 3; 5;7
Яблони и сизые дорожки, Изумрудно-яркая трава На берёзах – серые серёжки И ветвей плакучих кружева.
Листья падают в саду…В этот старый сад, бывало, Ранним утром я уйду И блуждаю, где попало. (И. Бунин)
Например, проведенный Н. Васютинским анализ стихотворений А.С. Пушкина с этой точки зрения показал, что размеры стихов распределены весьма неравномерно; оказалось, что Пушкин явно предпочитает размеры в 5, 8, 13, 21 и 34 строк (числа Фибоначчи).
Многими исследователями было замечено, что стихотворения подобны музыкальным произведениям; в них также существуют кульминационные пункты, которые делят стихотворение в пропорции золотого сечения.
В медицине: Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день – на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
Найдя сумму первых членов арифметической прогрессии, найдете, что вам надо купить 180 капель. Т.е. 2 пузырька лекарства.
Решение. Составим математическую модель задачи:
5, 10, 15,…,40, 40, 40, 35, 30,…,5
аn = а1 + d(n – 1),
40 = 5 + 5(n – 1),
n = 8,
Sn = ((a1 + aп)n)/2,
S8 = (5 + 40)/8:2 = 180,
180 капель больной принимал по схеме в первый период и столько же по второй период. Всего он принял 180 + 40 + 180 = 400 (капель), всего больной выпьет 400:250 = 1,6 (пузырька). Значит, надо купить 2 пузырька лекарства.
В спорте: Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день они проходи ли на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту в 5000 м
Решение. Составим математическую модель задачи:
1400, 1300, …, 1400 – 100(n – 1).
a1 = 1400; d = – 100, Sn = 5000.
Надо найти n.
Sn = (2a1 + d (n-1))n:2;
5000 = (2*1400-100 * (n – 1)) n:2; Условию задачи удовлетворяет
10000 = (2800 – 100 n + 100) n; n = 4 (при n = 25 аn = – 1000, но аn > 0)
10000 = (2900 – 100 n) n; Значит, альпинисты покорили
100 n2 – 2900 n + 10000 = 0; высоту за 4 дня.
n2 – 29 n + 100 = 0; n = 25, n = 4.
Ответ: за 4 дня.
В строительстве: Представьте, что вы – учетчик на стройке. Привезли большое количество бревен строевого леса. Нужно быстро определить, сколько бревен привезли, чтобы закрыть наряд шоферу.
Количество бревен легко подчитывается по формуле суммы арифметической прогрессии с разностью, равной единице.
Решение. Составим математическую модель задачи: 1, 2, 3, 4,…,12.
Это арифметическая прогрессия, а1 = 1, d = 1, аn = 12.
Надо найти n.
аn = a1 + d(n – 1);
12 = 1 + 1(n – 1); n = 12.
Sn = (a1 + an)•n:2;
Sn = (1 + 12)·12:2; Sn = 78.
В одной кладке находится 78 бревен.
Ответ: 78 бревен.
В банковских расчетах: a – первоначальный вклад; p – проценты p % годовых; t – срок хранения вклада.
1. В конце каждого года хранения вклада снимать проценты по вкладу, т.е. полученную прибыль в размере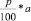 
руб. Математическая модель ситуации-конечная арифметическая прогрессия.
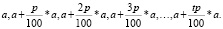
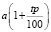руб. – формула простых процентов
2. Прийти в банк один раз – в конце срока хранения вклада. Математическая модель ситуации – конечная геометрическая прогрессия.
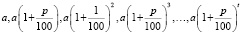
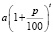– руб. формула сложных процентов.
Задачи на прогрессии с практическим содержанием из различных источников
Строительство:
Задача № 1 (КДР, математика 11 класс, январь 2014)
Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Решение:
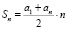
Sn = 240, a1 + an = 60
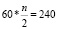
30n = 240
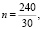
n = 8
Ответ: 8 дней
Задача № 2 (КДР, математика 11 класс, январь 2014)
Бригада маляров красит забор длиной 750 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 150 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Решение:
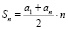
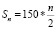, Sn = 750
75n = 750, n = 10
Ответ: 10 дней.
Задача № 3 («http://reShuege.ru/»)
Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней.
Решение:
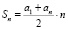
Sn = 500, a1 = 3
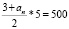
3 + an = 100..
n = 10
an = 97
Ответ: 97 метров
Задача № 4 (КДР, математика 11 класс, январь 2014)
Грузовик перевозит партию щебня массой 210 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено за девятый день, если вся работа была выполнена за 14 дней.
Решение:
S14 = 210, a1 = 2 n = 14
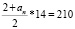
2 + a14 = 30
a14 = 28
28 = 2 + 13d
13d = 26
d = 2
a9 = 2 + 8d
a9 = 2 + 8*2
a9 = 18
Ответ: 18 тонн
Задача № 5 Студенты должны выложить плиткой мостовую. В 1 день они выложили 3 м2. Приобретая опыт, студенты каждый последующий день, начиная со второго, выкладывали на 2 м2 больше, чем в предыдущий. Сколько м2 уложат студенты в 15 день?
Решение:
a1 = 3, a2 = 5
a15 = a1 + 14d
a15 = 3 + 14*2
a15 = 31
a2 = a1 + d
5 = 3 + d
d = 2
Ответ: 31 тонн
Банковские расчеты:
Задача № 1 («http://reShuege.ru/»)
Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300 % по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?
Решение:
1) 
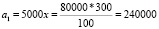
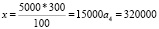
a2 = 20000
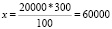
a3 = 80000
2) 
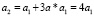2001 год
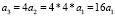2002 год
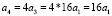2003 год
64*5000 = 320000
Ответ: 320000 рублей заработал бубликов за 2003 год
Задача № 2 («http://reShuege.ru/»)
Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200 % от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400 % от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?
Решение:
A) a1 = 5000 (2001 год)
B) b1 = 10000
a2 = a1 + 2a1 = 3a1 (2002 год) b2 = 5b1
a3 = 3a2 = 9a1 (2003 год) b3 = 25b1
a4 = 3a3 = 27a1 (2004 год) b4 = 125b1
a5 = 81a1 (2005 год) 125*10000 = 1250000$
a6 = 243a1 (2006 год)
243*5000 = 1215000$
1250000 – 1215000 = на 35000$ капитал одной компании был больше другой
Ответ: на 35000$
Задача № 3. Клиент взял в банке кредит в размере 50000 рублей на 5 лет под 20 % годовых. Какую сумму клиент должен вернуть банку в конце срока?
Решение:
t = 5
p = 20 %
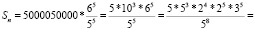
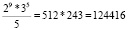
Ответ: 124416 рублей
Задача № 4. Два приятеля положили в банк по 10000 рублей каждый, причем первый положил деньги на вклад с ежеквартальным начислением 10 %, а второй- с ежегодным начислением 45 %. Через год приятели получили деньги вместе с причитающимися им процентами. Кто получил большую прибыль?
Решение:
a = 10000
p = 10 %
t = 4
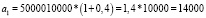
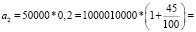
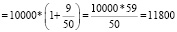
Ответ: Первый приятель получил большую прибыль
Медицина:
Задача № 1. Курс воздушных ванн начинают с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобыдостичь их максимальной продолжительности 1 ч 45 мин?
Решение:
an = 105, a1 = 15, d = 10
105 = 15 + 10(n – 1)
10n – 10 + 15 = 105
10n = 100
n = 10
Ответ: на 10 дней
Задача № 2. Отдыхающий, следуя совету врача, в первый день загорал 5 минут. А в каждый последующий день увеличивал время пребывания на солнце на 5 минут. НА какой день время пребывания на солнце будет равно 40 минут?
Решение:
a1 = 5, d = 5
аn = а1 + d(n + 1)
40 = 5 + 5(n – 1)
5n = 40
n = 8
Ответ: на 8-ой день
Задача № 3. Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день – на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства что составляет 250 капель?
Решение:
a1 = 5, d = 5, an = 40
40 = 5 + 5(n – 1)
5n – 5 + 5 = 40
5n = 40
n = 8
40*3 + 40 + 40 = 200 капель нужно
Ответ: 2 пузырька
Спорт:
Задача № 1. (Сборник конкурсных задач по математике под редакцией М.И. Сканави)
В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах – одно очко, за каждый последующий – на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?
Решение:
a1 = 1,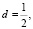 
Sn = 7
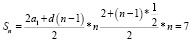
n2 + 3n – 28 = 0
n1 = –7 не удов. усл. задач n2 = 4
25 – 4 = 21
Ответ: в 21 раз
Задача № 2. В угловом секторе стадиона в первом ряду 7 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в 26-ом ряду?
Решение:
а1 = 7, d = 2
a26 = а1 + d*25 = 7 + 25*2 = 57
Ответ: в 26 ряду 57 мест
Другие задачи:
Задача № 1 («http://reShuege.ru/»)
Васе надо решить 490 задач. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.
Решение:
n = 14, S14 = 490
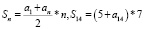
5 + а14 = 70
а14 = 65
Ответ: 65 задач
Задача № 2 («http://reShuege.ru/»)
Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.
Решение:
а1 = 10, Sn = 640,
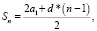
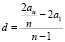
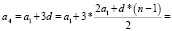
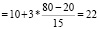
Ответ: 22 открытки
Задача № 3 («http://reShuege.ru/»)
Улитка ползет по дереву. За первую минуту она проползла 30 см, а за каждую следующую минуту – на 5 см больше, чем за предыдущую. За какое время достигнет улитка вершины дерева длиной 5,25 м, если считать, что движение начато от его основания?
Решение:
а1 = 30 n1 + n2 = –11
d = 5 n1 + n2 = 210
Sn = 525 n = 10
или
n = – 21 – не удов. усл. задач.
an = a1 + d*(n – 1) = 30 + 5(n – 1) = 25 + 5n
Sn = 1/2*(a1 + an)*n =
= 1/2*(30 + 25 + 5n)*n = 525
(55 + 5n)*n = 525*2
(11 + n)*n = 105*2
n2 + 11n – 210 = 0
Ответ: за 10 минут
Помимо того, что в данной работе рассмотрены задачи на прогрессии, взятые из различных источников по разным отраслям, меня заинтересовал вопрос: если в класс, в котором учится 27 учащихся, пришел заболевший ученик и пробыл среди данных учащихся весь учебный день, как быстро могут заболеть все учащиеся класса?
Попадая в благоприятные условия, бактерия делится, образуя две дочерние клетки; у некоторых бактерий деления повторяются через каждые 20 минут и возникают все новые и новые поколения бактерий. Заметим, что данная последовательность образует геометрическую прогрессию со знаменателем, равным 2. В сутках 1440 минут, каждые двадцать минут появляется новое поколение – за сутки 72 поколения. По формуле суммы n первых членов геометрической прогрессии, у которой b1 = 1, q = 2, n = 72, находим, что
S72 = 272 – 1 = 4 722 366 482 869 645 709 213 696 – 1 =
= 4 722 366 482 869 645 709 213 695.
Нетрудно заметить, что через час четвёртый член последовательности будет равен 8, через 2 часа- седьмой член последовательности будет равен 64 и т.д. Через 6 часов 19-ый член такой прогрессии будет равен 262144 и т.д. Таким образом, 262144 вырабатывается бактерий у одного заболевшего ребенка за 6 часов.
262144*2n = 4 722 366 482 869 645 213 696
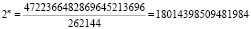
n = 54 поколения, а это 18 часов, т.е. за 18 часов попадания инфекции в организм человек заболевает. При благоприятных условиях на следующий день заболевших учащихся уже будет четверо и т.д., следовательно, 27 учащихся могут заболеть через 3 дня.
Заключение
В данной работе рассмотрены исторические сведения о практическом применении последовательностей, а именно арифметической и геометрической прогрессии; основные определения и формулы; рассмотрены примеры применения арифметической и геометрической прогрессии в различных отраслях, решены задачи из различных источников на применение арифметической и геометрической прогрессии с практическим содержанием по отраслям. Цели и задачи, поставленные нами перед написанием работы, достигнуты полностью.
Последовательности часто используется в разных отраслях нашей жизни. Мы сами не замечаем, как используем ее повседневно. Она помогает избегать нам неудачные ситуации, предугадывая правильный ответ. Знания по данной теме помогут мне в подготовке к ЕГЭ по математике, а также в различных жизненных ситуациях.
Библиографическая ссылка
Басько А.Г. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ АРИФМЕТИЧЕСКОЙ И ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИЙ // Старт в науке. – 2016. – № 2. ;URL: https://science-start.ru/ru/article/view?id=42 (дата обращения: 21.11.2024).