Введение.
Математика открывает свои тайны
только тому, кто занимается ею
ради её собственной красоты
Архимед
Хотя эта цитата была написана до нашей эры, она очень актуальна и в наши дни. В каждом человеке заложена природная любознательность, стремление познавать окружающий его мир. Так и мы решили для себя познавать ежегодно что-то новое и интересное. В прошлом учебном году мы познакомились с флексагонами, а что исследовать в этом учебном году? Самые гениальные открытия в науке способны кардинально изменить человеческую жизнь. В прошлом веке, например, люди научились «укрощать» электричество — и теперь мы не можем себе представить жизнь без всех этих удобных устройств, использующих электроэнергию. Но есть и такие открытия, которым мало кто придает значение, хотя они тоже сильно влияют на нашу жизнь.
Одно из таких «незаметных» открытий — фракталы.
Любопытную мысль приводит в своей книге "Фрактальная геометрия природы" американский математик Бенуа Мандельброт: «Почему геометрию часто называют холодной и сухой?»
Одна из причин заключается в том, что она неспособна достаточно точно описать форму облака, горы, дерева или берега моря. Облака – это не сферы, линии берега - это не окружности, и кора не является гладкой, а молния не распространяется прямолинейно. Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности». Рождение фрактальной геометрии принято связывать с выходом в 1977 году этой книги.
В связи с этим, по-моему мнению, данная наука молода и велик простор её изучения. Все, что существует в реальном мире, является фракталом – это и есть гипотеза.
Объект исследования: фракталы в математике и в реальном мире.
Предмет исследования: фрактальная геометрия.
Цель исследования: изучение новой ветви математики – фракталы, как основы применения её в реальной жизни.
Задачи исследования:
v изучение литературы по теме исследования;
v познакомиться с понятием, историей возникновения и исследованиями Б.Мандельброта, Г. Коха, В. Серпинского и др.;
v найти подтверждение теории фрактальности в окружающем нас мире;
v определить области применения фракталов;
v провести анкетирование для выяснения значимости теории фракталов;
v проведение эксперимента по созданию собственных фрактальных изображений.
Краткая история возникновения фракталов.
Так что же такое фрактал? Парадоксально, но общепринятого точного определения этого понятия не существует. Сам термин «фрактал» придумал Бенуа Мандельброт. Слово происходит от латинского «fractus», означающего «сломанный, разбитый». Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому».[2]
Фрактал — термин, означающий сложную геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. Для математических объектов, к которым оно относится, характерны чрезвычайно интересные свойства. В обычной геометрии линия имеет одно измерение, поверхность — два измерения, а пространственная фигура трехмерна. Фракталы же — это не линии и не поверхности, а, если можно это себе представить, нечто среднее. Это величина не целая, а дробная, а потому граница фрактальной фигуры не линия: при большом увеличении становится видно, что она размыта и состоит из спиралей и завитков, повторяющих в малом масштабе саму фигуру. Такая геометрическая регулярность называется масштабной инвариантностью или самоподобием. Она-то и определяет дробную размерность фрактальных фигур. Первые идеи фрактальной геометрии возникли в 19 веке. Георг Кантор (Cantor, 1845-1918) – немецкий математик, логик, теолог, создатель теории бесконечных множеств, с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек. Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками. Получалась, так называемая, Пыль Кантора (рис. 1).
Рис.1. Пыль Кантора

Рис. 2. Кривая Пеано
Джузеппе Пеано (Giuseppe Peano; 1858-1932) — итальянский математик изобразил особую линию. Он брал прямую и заменял ее на 9 отрезков длинной в 3 раза меньшей, чем длина исходной линии. Далее он делал то же самое с каждым отрезком. И так до бесконечности. Уникальность такой линии в том, что она заполняет всю плоскость (Рис.2) [1].
Классификация фракталов.
В основном фракталы классифицируют по трём группам:
1. Алгебраические фракталы
2. Стохастические фракталы
3. Геометрические фракталы
Рассмотрим подробнее каждую из них.
Алгебраические фракталы
Это самая крупная группа фракталов. Они оправдывают своё название, так как строятся на основе алгебраических формул, иногда довольно простых. К ним можно отнести фрактал Мандельброта (рис. 3), фрактал Ньютона (рис.4) и многие другие [4].


Рис. 3. Фрактал Мандельброта Рис.4. Фрактал Ньютона
Интересный факт, некоторые алгебраические фракталы поразительным образом напоминают изображения животных растений и других биологических объектов, вследствие чего получили название биморфов.
Геометрические фракталы
Фракталы этого класса самые наглядные. Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную - генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал. Примерами геометрических фракталов могут служить:
1) Кривая Коха. Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую
бесконечной длины, называемую снежинкой Коха. Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т.д.
2) Кривая Леви — фрактал. Предложен французским математиком П. Леви. Получается, если взять половину квадрата, а затем каждую сторону заменить таким же фрагментом, и, повторяя эту операцию, в пределе получим кривую Леви (рис. 5).
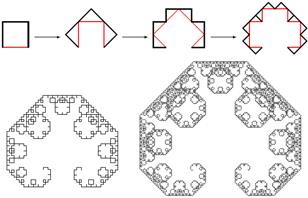
Рис. 5. Кривая Леви
3) Кривая Минковского — классический геометрический фрактал, предложенный Минковским. Инициатором является отрезок, а генератором является ломаная из восьми звеньев (два равных звена продолжают друг друга).
4) приведем пример кривой Пеано, для которой область, которую она заполняет на плоскости, имеет весьма причудливую форму. Это так называемый дракон Хартера-Хейтуэя.
5) Дерево Пифагора — разновидность фрактала, основанная на фигуре, известной как «Пифагоровы штаны». Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время Второй мировой войны, используя обычную чертёжную линейку.
6) Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Вацлавом Серпинским в 1915 году. Также известен как «решётка» или «салфетка» Серпинского
Также ещё одним несложным представителем геометрического фрактала является квадрат Серпинского. Строится он довольно таки просто: Квадрат делится прямыми, параллельными его сторонам, на 9 равных квадратов. Из квадрата удаляется центральный квадрат. Получается множество, состоящее из 8 оставшихся квадратов "первого ранга". Поступая точно так же с каждым из квадратов первого ранга, получим множесто, состоящее из 64 квадратов второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность или квадрат Серпинского.
Стохастические фракталы
Третьей крупной разновидностью фракталов являются стохастические фракталы, которые образуются путем многократных повторений случайных изменений каких-либо параметров. Термин "стохастичность" происходит от греческого слова, обозначающего "предположение".
В результате итерационного процесса получаются объекты очень похожие на природные фракталы — несимметричные деревья, изрезанные лагунами береговые линии островов и многое другое. Двумерные стохастические фракталы используются преимущественно при моделировании рельефа местности и поверхности моря. Эта группа фракталов получила широкое распространение благодаря работам Майкла Барнсли из технологического института штата Джорджия.
Типичный представитель данного класса фракталов "Плазма". Для ее построения возьмем прямоугольник и для каждого его угла определим цвет. Далее находим центральную точку прямоугольника и раскрашиваем ее в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число - тем более "рваным" будет рисунок. Если мы теперь скажем, что цвет точки это высота над уровнем моря - получим вместо плазмы - горный массив.
Применение фракталов
Фракталы находят все большее и большее применение в науке. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Вот несколько примеров:
Одни из наиболее мощных приложений фракталов лежат в компьютерной графике. Это фрактальное сжатие изображений.
В механике и физике фракталы используются благодаря уникальному свойству повторять очертания многих объектов природы. Фракталы позволяют приближать деревья, горные поверхности и трещины с более высокой точностью. Также фрактальную геометрию используют для устройств проектировании антенных. Впервые это было применено американским инженером Натаном Коэном, который жил тогда в центре Бостона, где была запрещена установка на зданиях внешних антенн. [6]
Фракталы в естественных науках. В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких как турбулентное течение жидкости, сложные процессы диффузии-адсорбации, пламя, облака и т.д. фракталы применяются для моделирования пористых материалов, например, в нефтехимии. Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков.
Заключение
Данная работа является введением в мир фракталов. Мы рассмотрели только самую малую часть того, какие бывают фракталы, на основе каких принципов они строятся.
В будущем планируем научиться строить алгебраические фракталы, когда более подробно изучим комплексные числа. Мы попробовали построить свои фрактальные изображения в программе Apophysis, также сделали несколько фракталов из бумаги и выполнили свои рисунки.
В нашей работе приведены далеко не все области человеческих знаний, где нашла свое применение теория фракталов. Следует отметить, что со времени возникновения теории прошло чуть более трети века, но за это время фракталы для многих исследователей стали внезапным ярким светом в ночи, которые озарил неведомые доселе факты и закономерности в конкретных областях данных. С помощью теории фракталов стали объяснять эволюцию галактик и развитие клетки, возникновение гор и образование облаков. При подготовке данной работы нам было очень интересно находить пxрименения теории на практике. Потому что очень часто возникает такое ощущение, что теоретические знания стоят в стороне от жизненной реальности.
Нам удалось показать, все, что существует в реальном мире, является фракталом. Мы убедились, что тому, кто занимается фракталами, открывается прекрасный, удивительный мир, в котором царят математика, природа и искусство. Очень надеемся, что после знакомства с нашей работой, вы, как и мы, убедитесь в том, что математика прекрасна и удивительна!
Библиографическая ссылка
Белозоров И.А., Третьякова Е.И. ПЕРВЫЕ ШАГИ В МИР ФРАКТАЛОВ // Старт в науке. 2020. № 3. ;URL: https://science-start.ru/ru/article/view?id=1920 (дата обращения: 04.07.2025).
