Введение
«Вдохновение нужно в поэзии,
как и в геометрии»
А.С. Пушкин
Изучая произведение А.С. Пушкина «Каменный гость», в 9-ом классе, мы обратили внимание на то, что в нем неоднократно упоминаются геометрические фигуры, например, треугольник.
«И кровь нейдет из треугольной ранки…»
Вернемся к геометрии. Математики называют треугольник двумерным симплексом. «Симплекс» - по латыни означает простейший. Трёхмерным симплексом называют треугольную пирамиду. Именно в силу своей простоты треугольник является основой многих измерений. Треугольник всегда имел широкое применение в практической жизни. Так, в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображение треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и других древних документах. Благодаря своей универсальности математика стала использоваться в естественных, гуманитарных науках и во всех сферах жизни человека [7].
И несмотря на то, что мы учимся в социально-гуманитарном классе, мы все-таки хотим расширить свои знания, особенно про свойства треугольника, которые могут пригодиться нам при сдаче ОГЭ и при подготовке к математическим олимпиадам, в которых мы тоже участвуем.
В прошлом учебном году мы работали над проектом, связанным с вневписанными окружностями и хотели как-то косвенно продолжить изучение этой темы. Поэтому мы решили остановиться на треугольниках, которые не входят в школьную программу и их замечательных точках и линиях. Ведь недаром А.С. Пушкин, чьё имя носит наше учебное заведение, прибегал в художественных произведениях к треугольнику, как источнику вдохновения. Итак, о простом и неисчерпаемом треугольнике…
Объект исследования: треугольники Жергона и Нагеля.
Предмет исследования: замечательные точки и линии в треугольнике.
Цель проекта: изучение и обобщение знаний о треугольниках за страницами учебника.
Задачи:
- изучить теоретический материал по теме: «О некоторых треугольниках и их замечательных точках и линиях, которых не встретишь в школьных учебниках»;
- повторить замечательные точки в треугольнике за школьный курс геометрии;
- расширить кругозор знаний по геометрии по замечательным точкам и линиям в треугольнике;
- научиться применять данные теоретические знания при решении задач планиметрии
- подготовить подборку задач для элективного курса по данной теме;
- создать буклет, как справочное пособие по данной теме;
- выпустить брошюру для элективного курса по математике «Замечательные линии и точки в треугольнике».
Мы выдвигаем гипотезу, что желание изучать и применять неизвестные теоремы при решении задач, может способствовать развитию интереса к геометрии, как науке.
Основная часть
Четыре замечательные точки треугольника, изучаемые в школе.
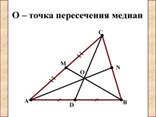
Переходя к основной части работы, мы начнём с замечательных точек треугольника. К числу таких точек, изучаемых в школьном курсе геометрии, относятся: рис.1(а,б,в,г) [1].
|
Рис.1(а), точка пересечения медиан, О – центр тяжести (барицентр) |
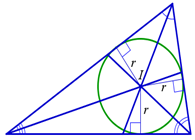
Рис. 1(б), точка пересечения биссектрис, I- центр вписанной окружности (инцентр) |
|
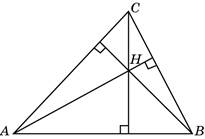
Рис. 1(в), точка пересечения высот H – ортоцентр |
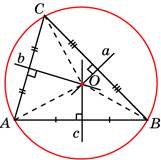
рис.1(г), точка пересечения серединных перпендикуляров к сторонам треугольника O - центр описанной окружности. |
На эти четыре точки было обращено особое внимание, и, начиная с XVIII века, они были названы «замечательными» или «особенными» точками треугольника.
Формулировки теорем Чевы и Менелая
Начало открытий замечательных точек треугольника, не изучаемых в школе, положил в 17 веке Джованни Чева (Ceva) (1648 - 1734) – итальянский математик. Основной заслугой Чевы является построение учения о секущих, которое положило начало новой – синтетической геометрии; оно изложено в сочинении "О взаимнопересекающихся прямых". Его теорема позволила открыть свойства замечательных точек треугольника, известных как точки Нагеля и Жергона [4].
Определение: отрезок, соединяющий вершину треугольника с точкой на противолежащей стороне или ее продолжении, называется чевианой (Рис.2) [4].
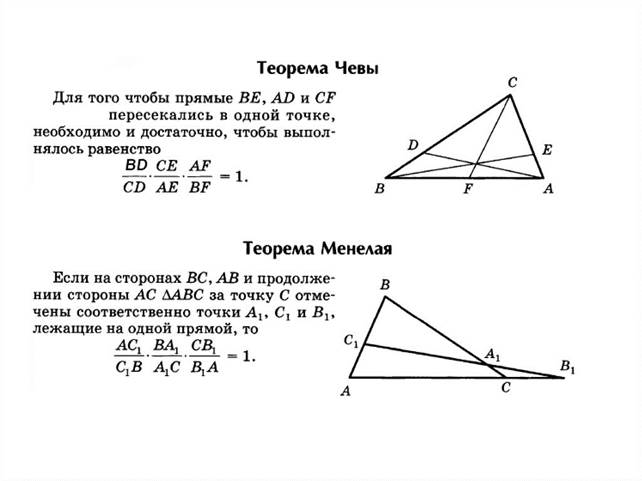
Рис. 2. Теорема Чевы и теорема Менелая
Прямая и окружность Эйлера [2]
Прямая Эйлера.
В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр и центр описанной окружности лежат на одной прямой, названной позже «прямой Эйлера» (Рис.3).
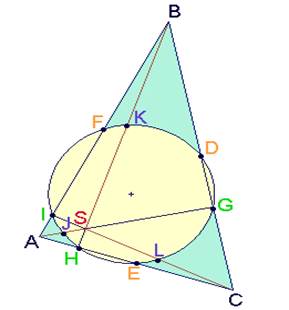
Рис. 3. Прямая и окружность Эйлера
Окружность Эйлера[2]
Середины сторон треугольника, основания его высот и середины отрезков, соединяющих ортоцентр с вершинами, лежат на одной окружности. Эта окружность называется окружностью девяти точек или окружностью Эйлера (Рис.3).
Свойство точек Жергонна и Нагеля [3]
Определение. Точкой Жергонна называется точка пересечения отрезков, которые соединяют вершины треугольника с точками касания сторон, противоположных этим вершинам, и вписанной в треугольник окружности. Пусть точка I — центр вписанной окружности треугольника ABC. Пусть вписанная окружность касается сторон треугольника BC, AC и AB в точках D, E и F соответственно. Точка Жергонна — это точка пересечения отрезков AD, BE и CF.
Докажем, что эти три отрезка действительно пересекаются в одной точке. Заметим, что центр вписанной окружности — это точка пересечения биссектрис углов треугольника ABC, а радиусы вписанной окружности ID, IE и IF перпендикулярны сторонам треугольника. Тем самым, имеем
три пары равных треугольников.
Произведения AF·BD·CE и AE·BE·CF равны, поскольку
BF=BD,CD=CE,AE=AF
следовательно, отношение этих произведений равно 1, и по теореме Чевы, отрезки пересекаются в одной точке.
Определение и свойство точки Нагеля [3]
Точка Нагеля — точка пересечения отрезков, соединяющих вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями.
· Точка Нагеля лежит на одной прямой с инцентром и центроидом, при этом центроид делит отрезок между точкой Нагеля и инцентром в отношении 2:1. Эта прямая
называется прямой Эйлера.
· Если точки T A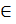 ВС,T B
ВС,T B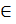 СА,T C
СА,T C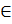 АВ таковы, что каждый из отрезков АT A,ВT B и СT C делит периметр треугольника пополам, то эти отрезки пересекаются в одной точке — точке Нагеля.
АВ таковы, что каждый из отрезков АT A,ВT B и СT C делит периметр треугольника пополам, то эти отрезки пересекаются в одной точке — точке Нагеля.
Треугольник Жергонна (для треугольника ABC) определяется тремя точками касания вписанной окружности на трёх сторонах. Эти вершины обозначим T A, T B и T C. Точка T A лежит напротив вершины A, точка TB напротив вершины В, точка TC напротив вершины С. Этот треугольник Жергонна T A T B TC известен также, как треугольник касаний треугольника ABC (Рис.4).
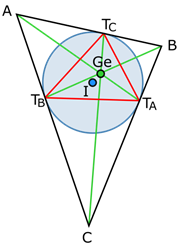
Рис. 4. Треугольник Жергонна
Свойства:
· Три прямые AT A, BT B и CT C пересекаются в одной точке – точке Жергонна.
· Точка Жергонна треугольника является точкой пересечения симедиан треугольника Жергонна.
Пусть, точки касания вписанной в данный треугольник окружности соединены отрезками, тогда получится треугольник Жергонна, и в полученном треугольнике проведены высоты. В этом случае прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно, ортотреугольник треугольника Жергонна и исходный треугольник подобны.
Теорема Жергонна. Пусть три чевианы AД, BE и CF пересекаются в точке K внутри треугольника ABC. Тогда выполняются следующие равенства:
1) 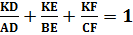
2) 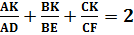
Доказательство. Поскольку выполняются очевидные равенства
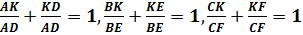
то равенства 1) и 2) эквивалентны. Докажем первое из них.
Рассмотрим отношения площадей треугольников
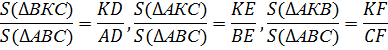
Здесь мы используем тот факт, что отношения площадей треугольников, имеющих общую сторону, равны отношениям их высот. Соответственно, отношение высот будет равно отношению длин параллельных отрезков, проведенных к общей стороне из противоположной вершины.
Теперь сложим отношения площадей:
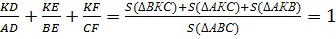
Треугольник Нагеля [3]
Треугольник Нагеля для треугольника ABC определяется вершинами TA, TB и TC, которые являются точками касания вневписанных окружностей треугольника ABC и точка TA противоположна стороне AВ, и т. д. (рис.5).
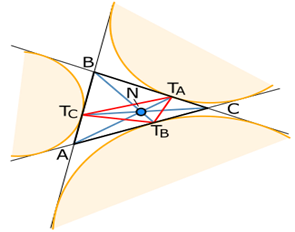
Рис. 5. Треугольник Нагеля
Свойства: описанная вокруг треугольника TA,TB,TC ,окружность называется окружностью Мандарта (частный случай эллипса Мандарта)
· Три прямые ATA, BTB и CTC делят периметр пополам и пересекаются в одной точке Нагеля.
Основные геометрические характеристики:
1) Если ширина треугольника Рёло равна а, то его площадь равна:
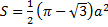
2) Периметр: 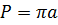
3) Радиус вписанной окружности: 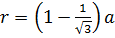
4) Радиус описанной окружности: 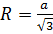
Построение:
Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выбирется произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух
Заключение
Для написания своей работы мы рассмотрели много теоретического материала.
Исследовали точки Жергонна и Нагеля, а также их треугольники и получили новые знания, использовал их при решении задач. Работая над темой, мы поняли, что, несмотря на то, что треугольник называют простейшей фигурой, он скрывает в себе еще много тайн, которые предстоит разгадать ученым.
Слова Жергонна о математических теориях: «Нельзя хвастаться тем, что ты сказал последнее слово в какой-либо теории, если не можешь объяснить ее несколькими словами первому встречному на улице» [2].
Обобщая всё вышесказанное, можем уверенно отметить, что сформулированная нами гипотеза, полностью подтверждена. Для нас решение задачи с использованием новых теорем и свойств доставляет огромное удовольствие. Тем более, что умение самостоятельно изучать дополнительный теоретический материал, обобщать и применять при решении задач поможет нам в дальнейшем.
Теоретический и практический материал мы постаралась изложить в работе так, чтобы она была легка в изучении, как учителю, так и ученику. А задачи, выбранные нами из учебника «Геометрия 7-9» под редакцией Атанасяна Л.С и задачников по геометрии, помогут в закреплении этой темы. Теоремы Чевы и Менелая казались сложными и непонятными на первый взгляд, но они оказались простыми и интересными. Теоремы Чевы и Менелая находят применение в задачах, в которых присутствуют секущие прямые. Они не изучаются в курсе 7-9 классов. Но решение с помощью теорем Чевы и Менелая более рационально, чем решение другими способами.
Мы считаем, что теоремы Чевы и Менелая должны быть включены в курс 7-9 классов, потому что они расширяют кругозор ученика, дают возможность решать задачи просто и легко. Исследование, проведенное нами, поможет хорошо сдать экзамены.
Знакомство с геометрическими фигурами, изучение которых не входит в рамки школьной программы, позволяет приобрести новые знания и иначе посмотреть на знакомые предметы.
Цель работы достигнута, и задачи решены, для успешной сдачи экзамена по геометрии сделан огромный шаг вперёд. Мы продолжим работать над этой темой и поучимся решать задачи на замечательные точки треугольника.
Библиографическая ссылка
Кирюшина Я.С., Кудряшева Д.Е. О НЕКОТОРЫХ ТРЕУГОЛЬНИКАХ И ИХ ЗАМЕЧАТЕЛЬНЫХ ТОЧКАХ И ЛИНИЯХ, КОТОРЫХ НЕ ВСТРЕТИШЬ В ШКОЛЬНЫХ УЧЕБНИКАХ // Старт в науке. 2020. № 3. ;URL: https://science-start.ru/ru/article/view?id=1917 (дата обращения: 16.01.2026).